赫尔德不等式详细证明

赫尔德不等式详细证明

$$\sum_{k=1}^{n} {\left | a_{k} b_{k} \right |} \leqslant (\sum_{k=1}^{n} {\left | a_{k} \right |}^p)^{1/p} (\sum_{k=1}^{n} {\left | b_{k} \right |}^q)^{1/q} \qquad\qquad(1)$$

其中数 $p>1$ 及 $q>1$ 具有关系 ：

$$\frac{1}{p} + \frac{1}{q} = 1 \qquad 即 \qquad p = \frac{q}{p-1} \qquad\qquad(2)$$

我们可以看到不等式(1)是齐次的，这意味着对于任意两个向量 $a = (a_{1}...a_{n})$ 与$b = (b_{1}...b_{n})$ 不等式(1) 成立，那么不等式(1)对于向量 $\lambda a$ 与 $\mu b$ 也成立(其中$\lambda$与$\mu$为任意数)因此对不等式(1)只要在：

$$\sum_{k=1}^{n} {\left | a_{k}\right |^{p}} = \sum_{k=1}^{n} {\left | b_{k}\right |^{q}} = 1 \qquad\qquad(3)$$
的情况下来证明就可以了.

补充 : $\lambda$ 和 $\mu$ 可取任意数,则总存在 $\lambda = \frac{1}{\sum_{k=1}^{n} {\left | a_{k}\right |^{p}}}$ 和 $\mu = \frac{1}{\sum_{k=1}^{n} {\left | b_{k}\right |^{q}}}$

于是假设条件 (3) 成立；我们可以来证明

$$\sum_{k=1}^{n} {\left | a_{k} b_{k} \right |} \leqslant 1 \qquad \qquad (4)$$
这里要引入 杨氏不等式

杨氏不等式证明:

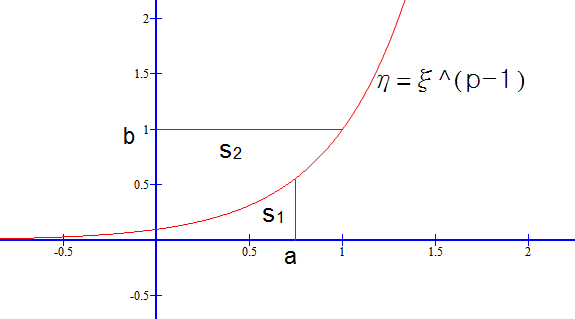
图1($\xi$取10)

我们研究由方程 $\eta = \xi^{p-1}(\xi>0)$ 或同样的方程 $\xi = \eta^{p-1}(\eta>0)$所确定的$(\eta,\xi)$平面上的曲线.由图(1)中显然可以看出，对于任意选取的正数$a$与$b$都有$S_{1} + S_{2} \geqslant ab$我们来计算$S_{1}$与$S_{2}$的面积：

$$S_{1} = \int_{0}^{a} \xi^{p-1}d\xi = \frac{a^{p}}{p}$$
$$S_{2} = \int_{0}^{b} \eta^{q-1}d\eta = \frac{b^{q}}{q}$$
于是,数的不等式
$$ab \leqslant \frac{a^{p}}{p} + \frac{b^{q}}{q} \qquad\qquad(5)$$ 成立.

以上为杨氏不等式的证明过程.
把不等式(5)中的$a$换成$\left | a_{k} \right |$，$b$换成$\left | b_{k} \right |$，并且按照$k$从1到$n$求和，注意式(2)和式(3)，我们可以的到:

$$\sum_{k=1}^{n} {\left | a_{k} b_{k} \right |} \leqslant 1 \qquad \qquad$$
具体详细证明过程如下:

补充:
先将$a,b$替换为$\left | a_{k} \right | ,\left |b_{k} \right |$得到下式

$$\sum_{k=1}^{n} {\left | a_{k} b_{k} \right |} \leqslant \frac{ \sum_{k=1}^{n} {\left | a_{k}\right |^{p}}}{p} + \frac{ \sum_{k=1}^{n} {\left | b_{k}\right |^{q}}}{q}$$
结合 式(3)
$$\sum_{k=1}^{n} {\left | a_{k} b_{k} \right |} \leqslant \frac{ 1}{p} + \frac{1}{q}$$
结合 式(2)
$$\sum_{k=1}^{n} {\left | a_{k} b_{k} \right |} \leqslant 1$$

这就证明了不等式(4)，也就证明了一般的赫尔德不等式.

注：证明摘自《函数论与泛函分析初步(第七版)》p29 并加入自己一些理解.