复合函数求导定义证明_【“数”你好看】求导

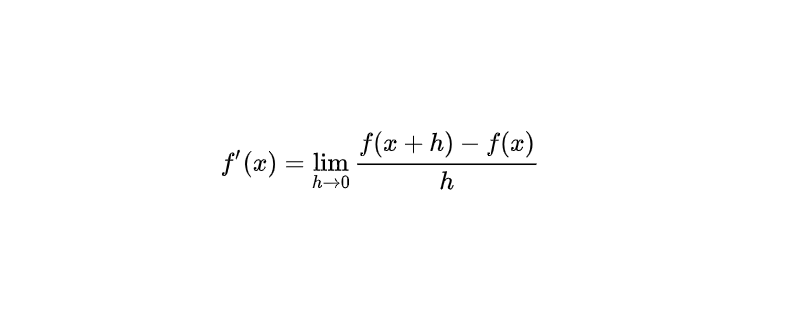
微积分的核心是极限(Limit)，求导(Derivative)是微积分的重要内容，本质就是求极限。导数公式有很多, 靠死记还是比较麻烦的，但这又是微积分的基础，不然接下去导数的应用(求切线、求法线、增减性、求极值、求凹凸性等)都没法学，更不用说导数的逆运算——求积分了。所以本文想系统的梳理一下求导法则及常见函数求导公式，争取利用最少的知识把下面公式都推导出来。

图：常见函数求导公式

---

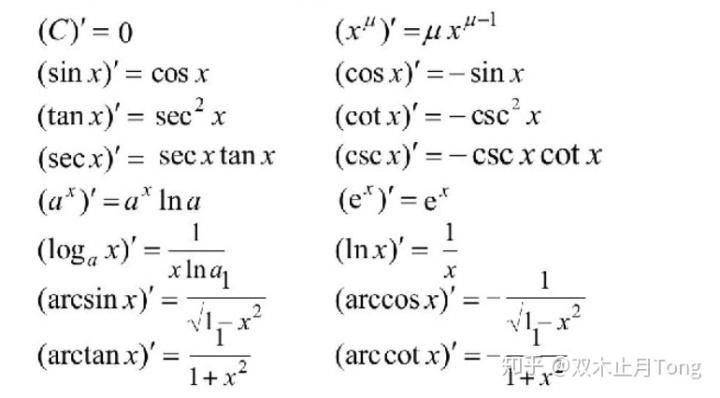
一、导数的定义

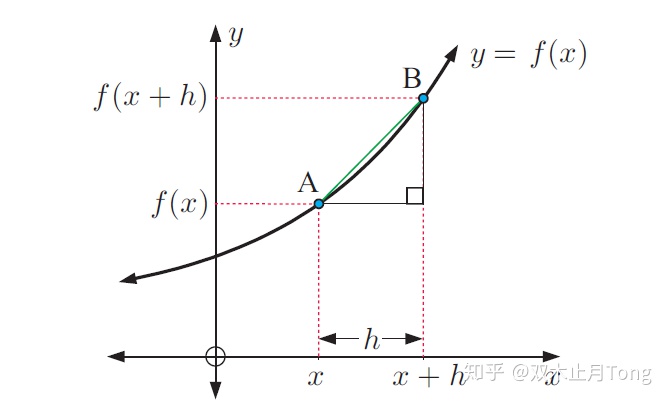
AB弦的斜率是

，当B点不断向A点靠近时，AB弦的斜率就变成了

在点A处的切线斜率(

可以类比平均速度和瞬时速度)，可以得到求导公式：

(Differentiation from first principle)

也可以用如下公式求

在

处的切线斜率：

那么根据上述定义，我们计算几个常见的求导公式。

（1）

（2）

因为

所以

（3）

注：

，

（4）

注：

（5）

又因为

所以

的导数等于其本身乘以在

处的导数，那么什么时候

的导数等于其本身呢？即

,

这里，令

,

所以

，

那么

注：根据

结合后面复合函数求导法则可以推导出

。

如果

不能理解，可以考虑推导

，然后再利用反函数求导得到

。

---

二、导数的四则运算及复合函数求导(The chain rule)

设

是关于x的两个可导函数，则

Scalar muptiplication rule:

Addition rule:

The product rule:

The quotient rule:

对于

与

直接根据定义就可以证明了，比较容易，下面证明求导的乘法与除法公式。

（1）The product rule

（2）The quotient rule

根据导数的乘法与除法法则，我们就可以计算

比如下面计算一下

其他三个也可以类似的推导得到，所以只需要记住

就够了。

接下去讲一个非常重要的复合函数求导——链式法则(The chain rule)：

若

在

处可导，且

在

处可导，则复合函数

的求导结果为：

.

用莱布尼兹表示，若

都是可导函数，则

学了链式法则，那么我们就可以推导

则根据

和链式法则有

---

三、隐函数求导

把能够写成

的函数称为显函数，但是有些情况下如

我们不能把x,y分离开，只知道x,y存在一定的关系

,把这样的称为隐函数。隐函数求导就是对

两边同时对x进行求导，且在求导过程中把y看成是一个关于x的函数，求导完成后只需要把

分离开来就得到了y关于x的导数。

接下去我们根据隐函数求导来推导一下求导公式表中的剩下公式。

（1）

，则

,两边对x进行求导可得：

,那么

。

又因为

,

所以

那么我们也可以知道

类似的我们也可以算得剩下三个反三角函数的导数

（2）

,则

,两边对x求导可得

,

又因为

所以

也可以类似得到，其中要用到两个三角恒等式

---

总结，我们通过导数的定义，推导了导数四则运算法则、链式法则，以及借助隐函数求导，把常见函数求导公式都推导了一遍。所以我们只需要记忆一些最基本的定义、最常见的函数求导就够了，其它复杂的忘记了现推一下也很快知道了。

这是我认为的推导常见函数求导公式比较顺的一个思路，可能还有更好的，欢迎交流讨论~

想了解更多国际数学课程知识，可参阅：

双木止月Tong：【国际数学课程】目录​zhuanlan.zhihu.com