c莫比乌斯函数_莫比乌斯变换

莫比乌斯变换是形如

这样一类从扩充的复平面到扩充的复平面的变换。我们比较好奇这样的变换长什么样子，以及这类变换在数学中广泛的联系

首先我们假设ad − bc ≠ 0 因为这时候映射是平凡

的。首先我们先把这样复杂的映射分解成一些简单的映射来分析一下。

我们看到第一个是平移，第二个我们把它称作复反演。第三个是伸缩加上旋转，第四类还是平移。所以对我们来说唯一不太熟悉的就是第二个，虽然它看起来很简单。

1，实反演

如果你熟悉反演的性质大概你马上就可以看出来可以分成关于原点反演可以看成实反演加上一个反射。如果我们是关于更一般的圆周做反演和复反演 ，就把圆周换成任一圆周 。

实反演其实和反射很像，严格来说反射是实反演的极限情况。

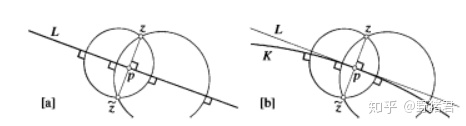
用初中平面几何的知识可以证明一些反演变换的基本性质。把过反演点的直线变成过反演点的直线，把不过反演点的直线变成过反演点的圆，由于反演变换和反射一样是对合的（两次之后变成自身）所以把过反演点的圆变成不过反演点的直线。把不过反演点的圆变成不过反演点的圆。注意看第一个图就是一维的球极投影

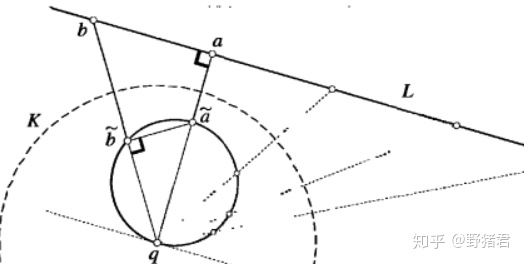
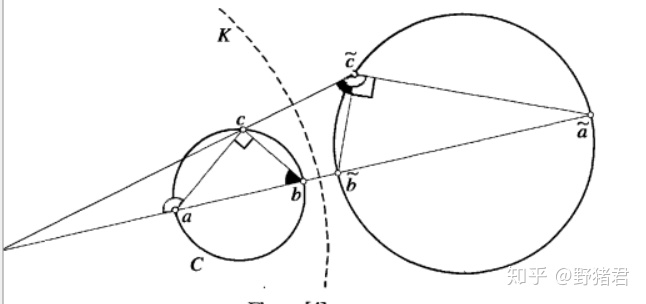
易说明反演是反角度的，一种是直接从平面几何直接去说，还有一种是因为复反演是解析的所以保持角度，实反演可以看成复反演反射一下所以反角度。

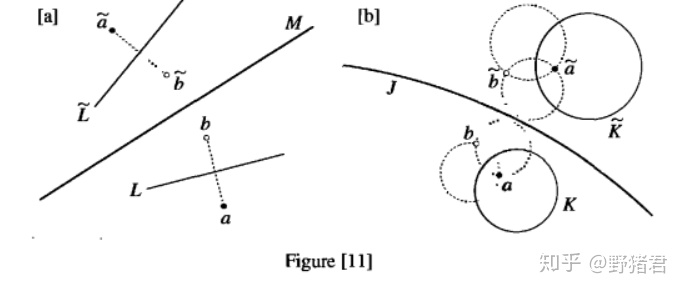
类似反射保持反射点，反演也保持反演点。因为反演点在所有与k正交的两个圆的交点，又根据保角性，易得。

我们定义完了二维的反演，我们不妨走的更远一点可以定义n维空间的反演，但对我们而言三维对我们来说足够了。作为应用我们可以发现球极投影是保持角度的或反角度的（看你怎么规定球面两个圆的夹角）

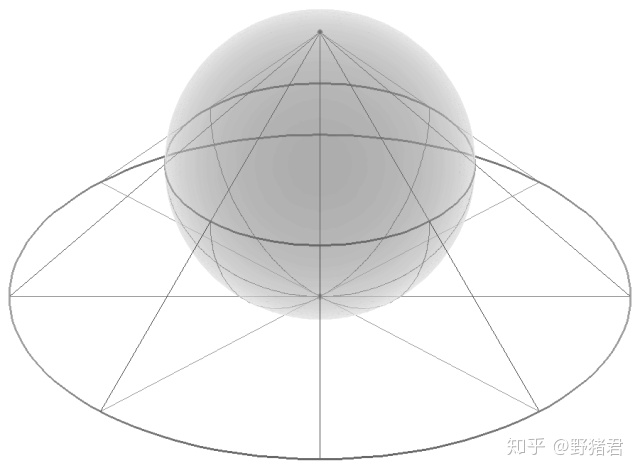
于是我们好奇一件事情，如果把平面上简单的映射用球极投影过去在球面上看是什么样子，如果把球面上简单的映射也利用球极坐投影来看是什么样子的。

2， 球面上的旋转和莫比乌斯变换以及四元数之间的联系

我们首先好奇复反演在球面上看长什么样子。

我们把这个看成一个实反演和反射 注意到实反演是关于球的反演点，注意到球极坐标变换其实是关于一个球面的反演 这个反演把球面变成平面，而关于平面的对称点其实是反射。 所以我们得到实反演是一个反射，不难看出反射用球极投影过去也是一个反射，对任意两个垂直的轴连续做反射的结果是对另外一个轴做180度的旋转。

不管如何我们最后都需要球极投影的具体表达式，让我们具体来给出。

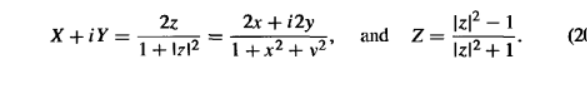
或者

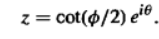
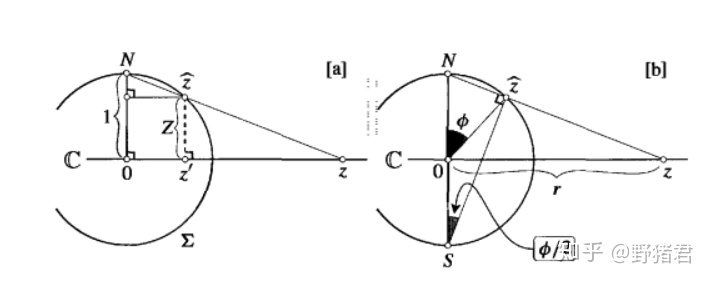
由第二种表示办法我们可以快速知道球面上的对径点映射过去满足

我们天真的想问球面上所有的旋转映射过去是不是莫比乌斯变换。 如果是具体是那种形式的莫比乌斯变换。 看起来莫比乌斯变换是四个系数，但是想要确定一个莫比乌斯变换三个自由度就够了，所以我们可以把莫比乌斯变换正规化

ad − bc = 1 其中

这样莫比乌斯变换就对应到了一个矩阵 注意到 每个元素乘以负一还表示同一个莫比乌斯变换。可以验证莫比乌斯变换到矩阵的对应关系确实是一个同态。

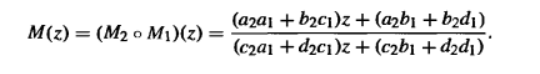
如果在复射影平面看，这个同态是显然的，因为复射影平面的线性变换要写成复数比的形式，这样写出来就是莫比乌斯变换，又因为矩阵乘法是可以通过现象映射的复合定义的，所以自然是一样的。

于是我们有了三种观点 平面上的莫比乌斯变换，矩阵的观点，还有球面的某种变换。如果把一个复数写成两个复数比的方式

就变成了

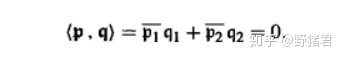
这告诉我们把球面对径点映射过去还是球面的对径点的映射一定对应了保内积的复矩阵！也就是SU(2)/(1,-1) 由于旋转是保持对径点的，所以我们猜测SU(2)/(1,-1)同构与SO3

首先注意到按照极点的旋转还是对应北极点的旋转，注意是半角的对角矩阵对应到极点的旋转。这让我们放心的猜测其实这个映射就是四元数旋转！

要验证这个映射就是四元数旋转 只需要在生成元上证明就够了。 也就是只需要验证对于标准四元数那四个矩阵验证就够了。 这件事情需要仔细算一下然后发现确实是对的。因为这三个矩阵对应的莫比乌斯变换都比较特殊所以计算量不是很大。

至于莫比乌斯变换的分类和一些其他形式的莫比乌斯变换在球面的情况和洛伦兹变换的联系还有分解成两到四个反演以及双曲几何的联系等以后有空再写了。，