1.双线性插值上采样
单线性插值函数

如上图所示,就是最简单的一种线性插值函数,就是求两点之间的直线方程,与初中的直线方程函数一样,首先知道
A
(
x
0
,
y
0
)
A(x_{0},y_{0})
A(x0,y0),
C
(
x
1
,
y
1
)
C(x_{1},y_{1})
C(x1,y1)两点的坐标,然后设B点坐标为
(
x
,
y
)
(x,y)
(x,y);从而得出

通过
y
0
y_{0}
y0,
y
1
y_{1}
y1可表示为

上面得出的函数即为AC两点的线性插值函数,B点的值可由插值函数得出,其本质就是在x方向进行了一次线性插值。
双线性插值,又称为双线性内插。在数学上,双线性插值是有两个变量的插值函数的线性插值扩展,其核心思想是在两个方向分别进行一次线性插值。双线性插值广泛应用在数值图像处理领域;其具体过程如下图所示:
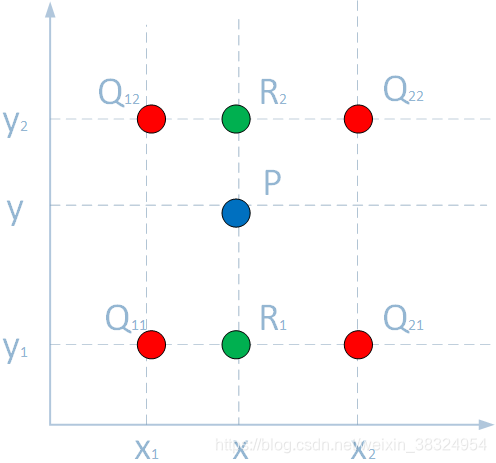
假如我们想得到未知函数 f 在点 P = (x, y) 的值,假设我们已知函数 f 在
Q
11
=
(
x
1
,
y
1
)
Q_{11} = ( x_1 , y_1 )
Q11=(x1,y1) 、
Q
12
=
(
x
1
,
y
2
)
Q_{12} = ( x_1 , y_2 )
Q12=(x1,y2) ,
Q
21
=
(
x
2
,
y
1
)
Q_{21} = ( x_2 , y_1 )
Q21=(x2,y1)以及
Q
22
=
(
x
2
,
y
2
)
Q_{22} = (x_2, y_2)
Q22=(x2,y2)四个点的值。最常见的情况,f就是一个像素点的像素值。首先在 x 方向进行线性插值,得到:

然后在 y 方向进行线性插值,得到
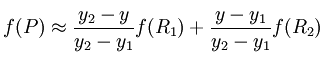
最后整理可得
 如果选择一个坐标系统使得 f 的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1),那么插值公式就可以化简为
如果选择一个坐标系统使得 f 的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1),那么插值公式就可以化简为
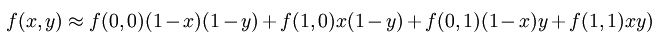
2.反卷积上采样
怎样上采样: 普通的卷积操作,会使得分辨率降低,如下图用33的卷积核去卷积44的输入得到2*2的输出。
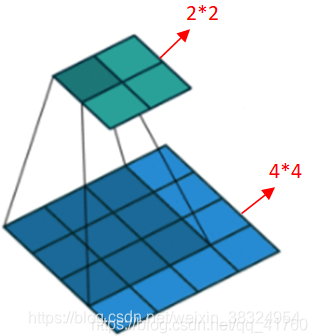
上采样的过程也是卷积,那么怎么会得到分辨率提高呢?之前看到卷积时有个保持输出与输入同分辨率的方法就是周围补0。但是只在四周补0会导致最边上的信息不太好,所以可以考虑把信息平均一下,在每个像素与像素之间补0。


3.反池化上采样
反池化可以用下图来理解,在池化时需要记录下池化的位置,反池化时把池化的位置直接还原,其他位置填0。

总结:
上面三种方法各有优缺,双线性插值方法实现简单,无需训练;反卷积上采样需要训练,但能更好的还原特征图;
参考博客:
https://blog.csdn.net/m0_37799466/article/details/103890049
https://blog.csdn.net/qq_41760767/article/details/97521397








 本文介绍了三种常见的图像上采样方法:双线性插值、反卷积上采样和反池化上采样。详细阐述了每种方法的工作原理及优缺点,并对比了它们在图像处理中的应用。
本文介绍了三种常见的图像上采样方法:双线性插值、反卷积上采样和反池化上采样。详细阐述了每种方法的工作原理及优缺点,并对比了它们在图像处理中的应用。
















 3923
3923

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








