目录
0.一些名词解释
模型参考自适应控制:MRAC
梯度法及MIT自适应控制律:查看上期博客,链接:直观理解-梯度下降及MIT自适应控制律_ayuan0211的博客-CSDN博客 https://blog.csdn.net/weixin_38342580/article/details/128302263?spm=1001.2014.3001.5502
https://blog.csdn.net/weixin_38342580/article/details/128302263?spm=1001.2014.3001.5502
以单一可调参数的可调增益为例,进行梯度法模型参考自适应解析。
1、基于MIT 律可调增益MRAC的原理
设被控对象为
式中为增益,位置或慢时变;
为已知的传递函数,且是稳定和最小相位的。(需要保证参考模型是稳定的)
则参考模型可取为 ,式中
为已知的参考模型增益。
辨识被控对象参数的结构如图:

可调增益MIT-MRAC系统结构
式中,中的
为微分算子。
取性能指标函数为
求J关于kc(t)的导数,即可得可调增益自适应律为:
确定学习步长为,则自适应律为
。
由图可知,系统的控制律为
2、MIT-MRAC实现步骤
已知G(s)
Step1 选择参考模型,即
Step2 选择参考输入信号和自适应增益
Step3 采样当前参考模型输出和系统实际输出
Step4 计算u(t)
Step5 ,返回Step3,继续循环。
3、代码实现
设稳定被控对象
未知,取仿真初始值为1。
选择参考模型为
取自适应增益,参考输入
为方波信号,其幅值r=0.6=,采用可调增益MIT-MRAC算法。
Matlab代码如下:
%可调增益MIT_MRAC chap3——02——MIT
clear all;
close all;
h=0.1;%积步步长
L=100/h;%仿真步数
num=[1];
den=[1,1,1];
n=length(den)-1;%被控对象阶次
kp=1;
[Ap,Bp,Cp,Dp]=tf2ss(kp*num,den);%传递函数转换为状态空间型
km=1;
[Am,Bm,Cm,Dm]=tf2ss(km*num,den);%参考模型
gamma=0.1;%自适应增益、调节步长
yr0=0;u0=0;e0=0;ym0=0;%初值
xp0=zeros(n,1);xm0=zeros(n,1)%状态向量初值
kc0=0;%可调节增益
for m=1:3
switch m
case 1
r=0.6;
case 2
r=1.2;
case 3
r=4.8;
end
yr=r*[ones(1,L/4) -ones(1,L/4) ones(1,L/4) -ones(1,L/4)];%输入信号
for k=1:L
time(k)=k*h;
xp(:,k)=xp0+h*(Ap*xp0+Bp*u0);
yp(k)=Cp*xp(:,k)+Dp*u0;%计算yp
xm(:,k)=xm0+h*(Am*xm0+Bm*yr0);
ym(k)=Cm*xm(:,k)+Dm*yr0;%计算ym
e(k)=ym(k)-yp(k);%e=ym-yp
kc=kc0+h*gamma*e0*ym0;%MIT自适应律
u(k)=kc*yr(k);%控制量
%更新数据
yr0=yr(k);
u0=u(k);
e0=e(k);
ym0=ym(k);
xp0=xp(:,k);
xm0=xm(:,k);
kc0=kc;
end
figure(m)
plot(time,ym,'r',time,yp,'g');
xlabel('t');
ylabel('y_m(t)、y_p(t)');
%axis([0 L*h -10 10]);
legend('y_m(t)','y_p(t)');
title(['r=',num2str(r)],'Color', 'm');
end
4、运行效果

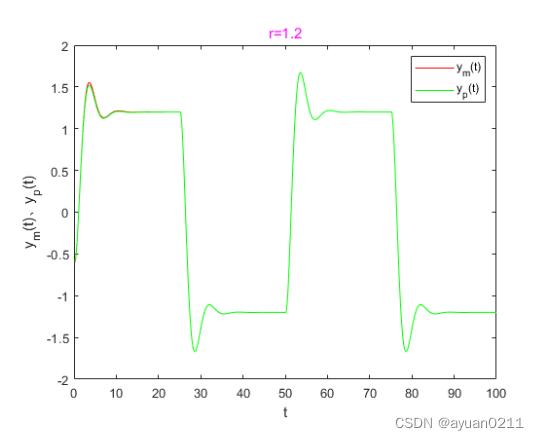

5、结论分析
仿真结果表明:当参考输入信号幅值较小时,闭环系统输出影响慢,当参考输入信号幅值较大时,系统可能会变得不稳定,由此可见系统的收敛速度和稳定性与参考输入信号的幅值密切相关。我们并不希望系统与输入信号幅值有关,因此对于输入信号全范围有所要求的系统,并不能使用此方法。
参考文件:系统辨识与自适应控制MATLAB仿真(第3版)庞中华、崔红编著








 该博客详细介绍了基于MIT律的可调增益模型参考自适应控制(MRAC)原理,包括系统结构、实现步骤和MATLAB代码实现。通过仿真展示了不同参考输入信号幅值对系统输出的影响,强调了参考输入幅值与系统收敛速度和稳定性之间的关系。
该博客详细介绍了基于MIT律的可调增益模型参考自适应控制(MRAC)原理,包括系统结构、实现步骤和MATLAB代码实现。通过仿真展示了不同参考输入信号幅值对系统输出的影响,强调了参考输入幅值与系统收敛速度和稳定性之间的关系。

















 4740
4740

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










