雷达系列论文翻译（三）：The normal-distributionstransform

The normal-distributionstransform

原文来自The Three-Dimensional Normal-Distributions Transform — an Efficient Representation for Registration, Surface Analysis, and Loop Detection 的第六章，其他章节内容有兴趣可以自行研究

用于表示曲面的NDT

第三章中讨论的距离传感器都输出点云:来自表面的一组空间采样点。此外，第5章中涉及的许多相关算法都是针对点云的。然而，使用点云来表示表面有许多限制。例如，点云不包含关于表面特征的明确信息，如方向、平滑度或孔洞。根据传感器配置，点云也可能效率低下，需要不必要的大量存储。为了在远离传感器的位置获得足够的样本分辨率，通常需要配置传感器，以便从靠近传感器的表面产生大量冗余数据。

正态分布变换可以描述为一种简单表示表面的方法。2003年，Biberand straer[7]首次提出它作为2D扫描配准的一种方法。Biber和straer后来在与Sven Fleck的联合论文[8]中对该方法进行了评价，也是在扫描配准和建图的背景下。该变换将点云映射到光滑的表面表示，描述为一组局部概率密度函数，每个概率密度函数描述表面的一部分的形状。

该算法的第一步是将扫描占据的空间细分为一个系列单元网格(2D的正方形，或3D的立方体)。基于单元内的点分布，为每个单元计算概率密度函数。每个单元中的PDF可以解释为单元内表面点$\overrightarrow{x}$的生成过程。换句话说，假设通过刻画这个分布，已经生成了$\overrightarrow{x}$的位置。假设参考表面点的位置是由一个D维正态随机过程产生的，那么已经测量到$\overrightarrow{x}$的可能性为
$$p(\overrightarrow{x})=\frac{1}{(2\pi {)}^{D/2}\sqrt{|\Sigma |}}exp(-\frac{(\overrightarrow{x}-\overrightarrow{\mu }{)}^T{\Sigma }^{-1}(\overrightarrow{x}-\overrightarrow{\mu })}{2})\text{\hspace{1em}(6.1)}$$
这里$\overrightarrow{\mu }$和$\Sigma$表示$\overrightarrow{x}$所处的单元格内参考扫描表面点云的均值向量和协方差矩阵。因子$((2\pi {)}^{D/2}\sqrt{|\Sigma |}{)}^{-1}$对函数进行了缩放，使其积分为1。实际上，它可以用常数$c_0$来表示。均值和协方差的计算方法如下
$$\overrightarrow{\mu }=\frac{1}{m}\sum _{k=1}^m{\overrightarrow{y}}_k\text{\hspace{1em}(6.2)}$$
$$\Sigma =\frac{1}{m-1}\sum _{k=1}^m({\overrightarrow{y}}_k-\overrightarrow{\mu })({\overrightarrow{y}}_k-\overrightarrow{\mu }{)}^T\text{\hspace{1em}(6.3)}$$
其中${\overrightarrow{y}}_{k=1,...,m}$为网格内包含的参考扫描点的位置。

正态分布用连续导数给出点云的分段光滑表示。每个PDF都可以看作是局部表面的近似，描述了表面的位置以及方向和平滑度。2D激光扫描及其相应的正态分布如图6.1所示。图6.2显示了矿井隧道扫描的三维正态分布。


由于目前的工作主要集中在正态分布上，让我们更仔细地研究一下单变量和多变量正态分布的特征。在一维情况下，正态分布的随机变量$x$有某个期望值$\mu$，关于该值的不确定性用变量$\sigma$表示。
$$p(x)=\frac{1}{\sigma \sqrt{2\pi }}exp(-\frac{(x-\mu {)}^2}{2{\sigma }^2})\text{\hspace{1em}(6.4)}$$
在一维情况下($D=1$)，方程6.1的多元概率密度函数$p(\overrightarrow{x}))$简化为上面的$p(x)$。在多维情况下，均值和方差由均值向量$\overrightarrow{\mu })$和协方差矩阵$\Sigma$来描述。协方差矩阵的对角元素表示每个变量的方差，非对角元素表示变量的协方差。图6.3说明了一维、二维和三维的正态分布。

在2D和3D情况下，表面的方向和平滑度可以由协方差矩阵的特征向量和特征值来确定。特征向量描述分布的主要成分；也就是说，对应于变量的协方差的主导方向的一组正交向量。根据方差的比例，2D正态分布可以是点状(如果方差相似)或线状(如果一个比另一个大得多)，或者介于两者之间。在3D情况下—如图6.4所示—正态分布可以描述为一个点或球体(如果所有方向上的方差大小相似)，一条线(如果一个方向上的方差比另两个方向上的大得多)，或者一个平面(如果一个方向上的方差比另两个方向上的小得多)。

NDT配准

当使用NDT进行扫描配准时，目标是找到当前扫描的位姿，使当前扫描的点位于参考扫描表面的可能性最大化。要优化的参数；即当前扫描的位姿估计的旋转和平移；可以用向量$\overrightarrow{p}$来表示，当前扫描表示为点云 χ = { x → 1 , . . . x → n } \chi = \{\overrightarrow{x}_1,...\overrightarrow{x}_n\} χ={x 1​,...x n​}。假设有一个空间变换函数$T(\overrightarrow{p},\overrightarrow{x})$将一个点通过为姿$\overrightarrow{p}$移动一个点$\overrightarrow{x}$。给定一些扫描点的PDF$p(\overrightarrow{x})$(例如，公式6.1)，最佳位姿$\overrightarrow{p}$应该是最大化似然函数的位姿
$$\Psi =\prod _{k=1}^{n}p(T(\overrightarrow{p},{\overrightarrow{x}}_k))\text{\hspace{1em}(6.5)}$$
或者等效地，最小化$\Psi$的负对数似然:
$$-log\Psi =-\sum _{k=1}^{n}log(p(T(\overrightarrow{p},{\overrightarrow{x}}_k)))\text{\hspace{1em}(6.6)}$$

PDF不一定被限制为正态分布。任何局部捕捉表面点的结构并对对外点具有鲁棒性的PDF都是合适的。对于远离平均值的点，正态分布的负对数似然性在没有边界的情况下增长。因此，扫描数据中的异常值可能对结果有很大影响。在这项工作中(如Biber，Fleck和straer[8]的论文)，使用了正态分布和均匀分布的混合:
$$\bar{p}(\overrightarrow{x})=c_{1}exp(-\frac{(\overrightarrow{x}-\overrightarrow{\mu }{)}^T{\Sigma }^{-1}(\overrightarrow{x}-\overrightarrow{\mu })}{2})+c_2{p}_o\text{\hspace{1em}(6.7)}$$

其中$p_o$是异常值的预期比率。使用这个函数，外点的影响是有限的。这如图6.5所示。

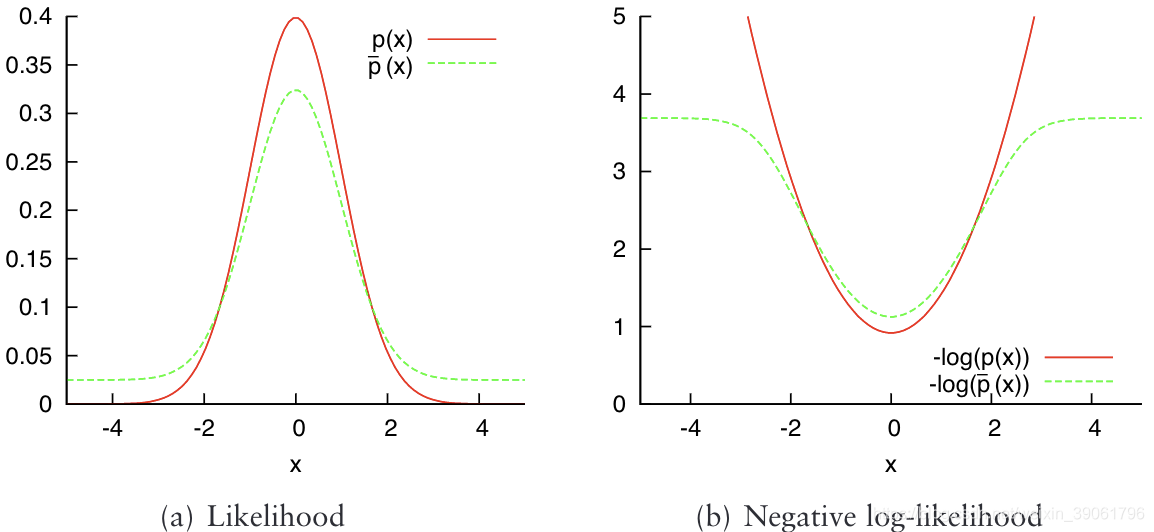
常数$c_1$和$c_2$可以通过要求̄$p(\overrightarrow{x})$在一个单元所跨越的空间内积分等于1来确定。

待优化的对数似然能量函数的和由形式为对数的项组成$-log(c_{1}exp(-(\overrightarrow{x}-\overrightarrow{\mu }{)}^T{\Sigma }^{-1}(\overrightarrow{x}-\overrightarrow{\mu }))/2)+c_2)$。这些项没有简单的一阶和二阶导数。然而，图6.5(b)表明对数似然函数又可以用高斯函数来近似。形式为̄$\bar{p}(x)=-log(c_{1}exp(-x^2/(2{\sigma }^2))/2)+c_2)$的函数可以用高斯̃分布函数$\tilde{p}(x)=d_{1}exp(-d_2{x}^2/(2{\sigma }^2))+d_3$近似，拟合参数$d_i$可以通过要求近似的高斯分布函数$\tilde{p}(x)$在$x=\mu$，$x=\mu +\sigma$以及$x=\infty$处与原始分布$p(x)$一致来求得
$$\begin{gathered} d_3=-log(c_2) \\ {d}_1+d_3=-log(c_1+c_2) \\ {d}_2=-2log((-log(c_{1}exp(-1/2)+c_2)-d_3)/d_1)\text{\hspace{1em}(6.8)} \end{gathered}$$

使用这种高斯近似，当前扫描的一个点对NDT分数函数的影响为
$$\tilde{p}({\overrightarrow{x}}_k)=-d_{1}exp(-\frac{d_2}{2}({\overrightarrow{x}}_k-{\overrightarrow{\mu }}_k{)}^T{\Sigma }^{-1}({\overrightarrow{x}}_k-{\overrightarrow{\mu }}_k))\text{\hspace{1em}(6.9)}$$
其中${\overrightarrow{\mu }}_k$和${\Sigma }_k$是${\overrightarrow{x}}_k$所在的NDT网格的均值和协方差。这种NDT分数函数比等式6.7的对数具有更简单的导数，但是当用于优化时仍然表现出相同的一般性质。请注意，公式6.9中省略了$d_3$项。当使用NDT进行扫描配准时，这是不需要的，因为它只是给分数函数增加了一个恒定的偏移量，而不会改变其形状或被优化的参数。

给定一组点 χ = { x → 1 , . . . , x → n } \chi = \{ \overrightarrow{x}_1,...,\overrightarrow{x}_n \} χ={x 1​,...,x n​}，一个位姿$\overrightarrow{p}$，一个变换函数$T(\overrightarrow{p},\overrightarrow{x})$通过位姿$\overrightarrow{p}$对点$\overrightarrow{x}$进行变换，当前参数向量的NDT得分函数$s(\overrightarrow{p})$为
$$s(\overrightarrow{p})=-\sum _{k=1}^n\overrightarrow{p}(T(\overrightarrow{p},{\overrightarrow{x}}_k))\text{\hspace{1em}(6.10)}$$
这对应于当点被$\overrightarrow{p}$变换后落在参考扫描表面上的可能性。

似然函数需要协方差矩阵的逆${\Sigma }^{-1}$。如果网格单元中的点完全共面或共线，则协方差矩阵是奇异的，不能求逆。在三维情况下，由三个点或更少点计算的协方差矩阵总是奇异的。因此，PDF仅针对包含五个以上点的单元格进行计算。此外，作为对数值问题的预防措施，$\Sigma$只要被发现是接近奇异的，就会稍微膨胀。如果最大特征值${\lambda }_3$比${\lambda }_1$或${\lambda }_2$大100倍以上，那么较小的特征值${\lambda }_j$被${\lambda }_j^{{}^{\prime }}={\lambda }_3/100$代替。用矩阵${\Sigma }^{{}^{\prime }}=V{\Lambda }^{{}^{\prime }}V$代替$\Sigma$，其中$V$包含$\Sigma$的特征向量并且
$${\Lambda }^{{}^{\prime }}=\left[\begin{array}{ccc}{\lambda }_1^{{}^{\prime }}& 0& 0\\ 0& {\lambda }_2^{{}^{\prime }}& 0\\ 0& 0& {\lambda }_3\end{array}\right].\text{\hspace{1em}(6.11)}$$
牛顿算法可以用来寻找优化的参数$\overrightarrow{p}$。牛顿法迭代求解方程$H\Delta \overrightarrow{p}=-\overrightarrow{g}$，其中$H$和$\overrightarrow{g}$是$s(\overrightarrow{p})$的Hessian矩阵和梯度向量。在每次迭代中，增量$\Delta \overrightarrow{p}$被添加到当前位姿估计中，因此$\overrightarrow{p}\leftarrow \overrightarrow{p}+\Delta \overrightarrow{p}$。

为了简洁起见，让${\overrightarrow{x}}_k^{{}^{\prime }}=T(\overrightarrow{p},{\overrightarrow{x}}_k)-{\overrightarrow{\mu }}_k$。换句话说${\overrightarrow{x}}_k^{{}^{\prime }}$是${\overrightarrow{x}}_k$被当前的位姿参数变换后距离它所属的网格中心的距离向量。可以写出梯度向量$\overrightarrow{g}$的项${\overrightarrow{g}}_i$
$$g_i=\frac{\delta s}{\delta p_i}=\sum _{k=1}^n{d}_1{d}_2{{\overrightarrow{x}}_k^{{}^{\prime }}}^T{\Sigma }_k^{-1}\frac{\delta {\overrightarrow{x}}_k^{{}^{\prime }}}{\delta p_i}exp(\frac{-d_2}{2}{{\overrightarrow{x}}_k^{{}^{\prime }}}^T{\Sigma }_k^{-1}{\overrightarrow{x}}_k^{{}^{\prime }})\text{\hspace{1em}(6.12)}$$
Hessian矩阵$H$的项$H_{ij}$为

NDT分数函数的梯度(6.12)和Hessian矩阵(6.13)以相同的方式表达，不管配准是在2D还是在3D(或任何其他维度)中进行。它们同样独立于正在使用的转换表示。另一方面，方程6.12和6.13中$ \overrightarrow{x}^{’}$的一阶和二阶偏导数依赖于变换函数。不同选择的$T$的2D和3D配准之间的差异将在第6.2.1和6.2.2节中描述。

在之前的几篇关于NDT扫描配准的出版物[7，47，56，63，66，88]中，评分函数是直接使用正态分布的PDF中的高斯形式的和来定义的。尽管从概率的角度来看，这样的公式不太令人满意，但最终结果与使用混合模型对数似然的高斯近似(6.9)的结果(6.7)非常相似。

算法2描述了如何使用NDT方法配准两个点云$\mathcal{X}$和$\mathcal{Y}$。

2D-NDT

对于2D配准，有三个变换参数需要优化。设$\overrightarrow{p}=[t_x,t_y,\varphi {]}^T$，其中$t_x$和$t_y$为平移参数，$\varphi$为旋转角度。使用逆时针旋转，2D变换函数是
$$T_2(\overrightarrow{p},\overrightarrow{x})=\left[\begin{array}{cc}cos\varphi & -sin\varphi \\ sin\varphi & cos\varphi \end{array}\right]\overrightarrow{x}+\left[\begin{array}{c}{t}_x\\ t_y\end{array}\right]\text{\hspace{1em}(6.14)}$$
利用这个2D变换函数，由雅各比矩阵的$i$列给出了用于计算方程6.12中梯度的一阶导数$\delta {\overrightarrow{x}}^{{}^{\prime }}/\delta {\overrightarrow{p}}_i$
$$J_2=\left[\begin{array}{ccc}1& 0& -x_{1}sin\varphi -x_{2}cos\varphi \\ 0& 1& x_{1}cos\varphi -x_{2}sin\varphi \end{array}\right].\text{\hspace{1em}(6.15)}$$
等式6.13中使用的二阶导数为

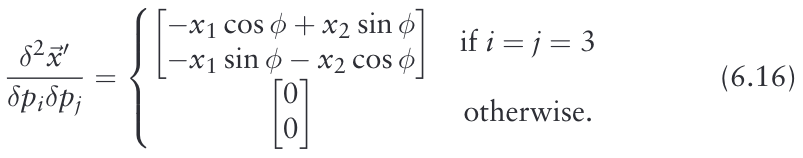
3D-NDT

2D与3DNDT配准的主要区别在于空间变换函数 $T(\overrightarrow{p},\overrightarrow{x})$及其偏导数。在2D中，旋转用绕原点旋转的角度的单个值来表示，最明显的变换函数是方程6.14中的一个。在3D情况下，有几种方法可以表示旋转，如第2.2节所述。

在我们先前的三维NDT工作[63，66]中，使用了轴/角旋转表示。然而，这样做给优化问题增加了一个额外的变量，并且需要额外的约束来保持旋转轴的单位长度。牛顿优化方法是一种迭代方法，在每次牛顿迭代后，只需对旋转表示重新归一化，就可以强制实施单位轴约束。然而，当牛顿更新方向偏离到位姿参数空间的不可行区域时，这种策略仍然会导致问题，这可以解释先前结果中的一些不一致。为完整起见，附录B.2中提供了轴/角度转换函数及其导数。

在下文中，将使用三维欧拉角，尽管这种旋转表示存在潜在的问题。这些优点——数值优化过程不需要进行约束，导数也稍微不那么复杂——被评估为超过万向节锁的风险，万向节锁只会在大角度出现，以至于局部配准过程无论如何都很可能失败。使用欧拉角，有六个变换参数需要优化:三个用于平移，三个用于旋转。可以使用六维参数向量${\overrightarrow{p}}_6=[t_x,t_y,t_z,{\varphi }_x,{\varphi }_y,{\varphi }_z]$对位姿进行编码。

使用欧拉序列$z-y-x$，3D变换函数为
$$\begin{gathered} T_E({\overrightarrow{p}}_6,\overrightarrow{x})=R_x{R}_y{R}_z\overrightarrow{x}+\overrightarrow{t} \\ =\left[\begin{array}{ccc}{c}_y{c}_z& -c_y{s}_z& s_y\\ c_x{s}_z+s_x{s}_y{c}_z& c_x{c}_z-s_x{s}_y{s}_z& -s_x{c}_y\\ s_x{s}_z-c_x{s}_y{c}_z& c_x{s}_y{s}_z+s_x{c}_z& c_x{c}_y\end{array}\right]\overrightarrow{x}+\left[\begin{array}{c}{t}_x\\ t_y\\ t_z\end{array}\right]\text{\hspace{1em}(6.17)} \end{gathered}$$
其中$c_i=cos{\varphi }_i$，$s_i=sin{\varphi }_i$ .方程6.17的一阶导数$\delta T_E({\overrightarrow{p}}_6,\overrightarrow{x})/\delta p_i$为

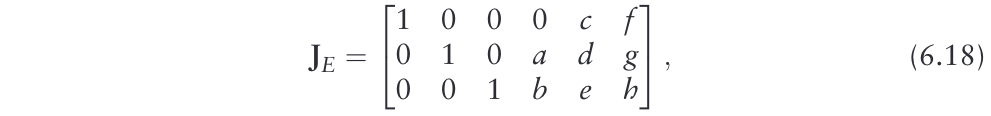
这里

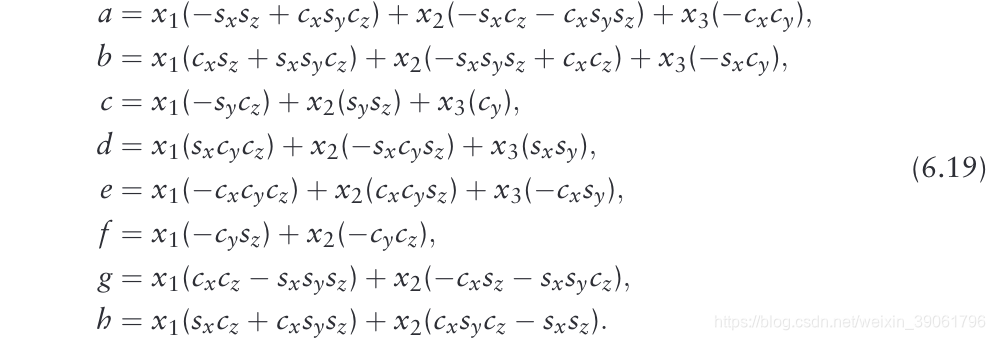
二阶导数${\delta }^2{T}_E({\overrightarrow{p}}_6,\overrightarrow{x})/\delta p_i\delta p_J$为

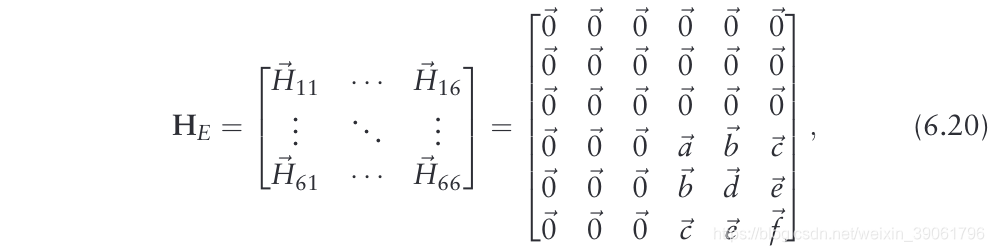
这里

通过对小角度使用以下的近似计算，可以大大简化计算:
$$\begin{gathered} sin\varphi \approx \varphi \\ cos\varphi \approx 1 \\ {\varphi }^2\approx 0\text{\hspace{1em}(6.22)} \end{gathered}$$
对于小于$10°$的角度，这些近似值可以认为是精确的。对于正弦函数，在$14°$角时近似误差达到$1$。对于余弦，同样的误差出现在$8.2°$角。当使用小角度近似时，计算变换函数及其导数更快，但是在某些情况下，与使用方程6.17相比，使用近似的配准不那么鲁棒。附录B.1中提供了相应的小角度近似的闭环函数。在时间要求严格的应用中，推荐使用近似公式，尽管差异很小。

对于非线性优化的许多应用，通常使用Hessian矩阵的数值近似代替解析的Hessian矩阵，因为Hessian矩阵无法解析计算，或者计算起来过于昂贵。然而，由于NDT评分函数的Hessian矩阵可以解析计算，并且其大部分元素为零，因此不使用近似值是有利的。为了完整起见，使用Hessian的BFGS近似[91]的准牛顿法已经与牛顿法和方程6.13的Hessian法进行了比较。使用拟牛顿法时，鲁棒性较低。一些准牛顿结果可以在附录C中找到。

3D-NDT扩展

本节描述了3-DNDT的一些扩展，旨在更好地表示潜在的表面。3D-NDT最重要的参数是网格尺寸。任何比单元尺寸小得多的特征都会被描述其周围局部表面形状的函数所模糊，因为正态分布是单峰的。选择一个太大的网格尺寸通常会导致不太精确的配准。另一方面，一个网格的影响区域只延伸到它的边界。也就是说，该单元将只对其边界内的扫描点的评分函数有贡献。这样做的一个结果是，如果网格尺寸太小，只有当两次扫描最初靠得很近时，配准才会成功。另一个问题是，对于较小的网格，可能根本不使用具有低点密度的部分扫描，因为每个网格至少需要五个点来计算可靠的协方差矩阵。使用更小的网格也需要更多的内存。因此，网格的最佳大小和分布取决于输入数据的形状和密度。他们还取决于应用对扫描表示保真度的要求。

使用正方形或立方体单元格的固定尺寸网格会给用户带来选择好的网格大小的任务。更灵活的网格结构是更可取的:在可能的情况下使用大网格，在单个正态分布不能令人满意地描述表面的地方使用更精细的网格划分。本节介绍了创建NDT网格结构和相关似然函数的多种替代方法。

固定尺寸离散化

抛开刚才提到的缺点，使用固定网格单元的好处是初始化和使用网格结构的开销非常小。每个网格只需要计算一组参数，每个网格的定位很简单。对于算法的性能更为重要的是，点到网格的查找可以在恒定时间内非常快速地完成，因为网格可以存储在一个简单的数组中。

八叉树离散化

八叉树是一种常用的树结构，可用于存储三维空间的分层离散。在八叉树中，每个节点代表空间的一个有界区间。每个内部节点有八个子节点，代表其父节点的空间分区的一致的不重叠的子区间。当创建八叉树时，根节点的大小被调整为包含整个参考扫描。然后递归地构建树，分割包含超过一定数量点的所有节点。所有数据点都包含在八叉树的叶节点中。八叉树非常类似于KD树，但是每个内部节点有八个而不是两个子节点。

如前所述，3D-NDT的八叉树版本从固定的规则网格开始，区别在于每个网格都是八叉树的根节点。分布方差大于某一阈值的所有网格被递归分割，形成八叉树森林。

对于NDT的效率来说，点对网格的查找是非常重要的，这也是使用八叉树森林的主要原因，而不是使用根节点跨越所有扫描的单个八叉树。对于许多类型的扫描数据，可以指定一个合理的基本网格大小，这样只需要分割扫描表面特别不均匀的部分中的几个网格。因此，对于大多数点来说，找到正确的网格只需要一次数组访问，而对于每个点来说，一次转换八叉树将花费更多的时间。一个森林比一棵树需要更多的内存，特别是当每棵树的根节点的网格很小时，但是这种影响对于本文介绍的实验来说可以忽略不计。

迭代离散化

另一种选择是，使用每次运行的最终为姿态作为下一次运行的初始位姿，以更高的网格分辨率执行多次NDT。第一次运行有助于将对齐不良的扫描更紧密地结合在一起，之后的运行改善了粗略的初始匹配的精度。

自适应聚类

一种更具适应性的离散化方法是使用聚类算法，该算法根据扫描点的位置将扫描点分成多个聚类，并为每个聚类使用一个NDT网格。

一种易于实现的通用聚类算法为k-means聚类[29]，其工作原理如下。初始化$k$个聚类中心，扫描点随机分配给聚类。聚类算法迭代推进。在每一步中，每个聚类的中心点是从它当前包含的点的质心计算出来的。每个点都被分配到最近的聚类中心。重复这两个步骤，直到在两次迭代之间没有更多的点改变聚类，或者直到改变的数量低于某个阈值。为了获得良好的聚类分布，没有特别大或者特别小的聚类，初始分布应均匀分布在扫描所占的空间体积上。然后聚类算法尝试将聚类移动到它们应该在的地方。使用这种离散化方法，必须预先确定网格的数量$k$，但算法可以自动确定每个网格的大小，这与手动确定网格大小的其他离散化方法不同。图6.6显示了一个使用k均值聚类的网格分布示例。

链接网格

使用第6.2节中描述的NDT公式，位于没有被参考扫描表面占据的网格中的扫描点被丢弃。不使用这种方法，而是将最近的被占用的网格用于这些点。这增加了网格的影响范围。通常情况下，对于超出网格边界的部分，网格的函数值几乎为零，在这种情况下，它对分数没有实质性的贡献。但有些情况下(例如，对于点分布具有较大方差的网格)，网格外的分布函数基本上不为零。

实现这种最近占用网格策略的一种方法是“链接单元”:让NDT网格中的每个网格存储一个指向最近网格单元的指针，并在网格中查询对应于某个点的网格时使用这些指针。这个实现已经在NDT配准[63，64，66]的早期工作中使用过。具有相同效果的另一种实现是在一个KD树搜索结构中只存储NDT网格的已占用网格，在KD树中查询最近的网格。如果有很多未被占用的网格则后者是更好的方法，并且是本工作中使用的实现。这种方法在下文中仍称为“链接网格”。

双线性插值

将空间细分为离散的网格会导致网格边缘的表面表示不连续，这有时会造成问题。在最初的2D-NDT实现[7]中，通过使用四个重叠的2D网格，离散化效果被最小化。类似的方法是使用四个(在2D)或八个(在3D)相邻网格的正态分布，每个网格的贡献权重由三线性插值(在2D为双线性)确定。换句话说，每个点的得分函数(6.9)被替换为

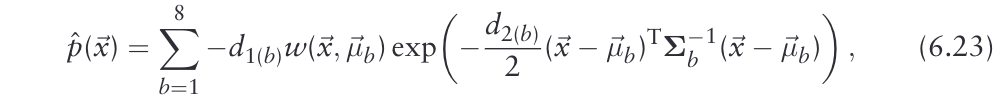
其中${\overrightarrow{q}}_b$、${\Sigma }_b$和$d_{i(b)}$是最接近$\overrightarrow{x}$的八个网格的均值、协方差和尺度参数；$w(\overrightarrow{x},\overrightarrow{\mu })$是一个三线性插值权重函数。等式6.23具有类似于Biber和Straber方法的平滑效果，而不需要计算更多的概率函数。效果如图6.7所示。

因为每个点需要评估多达八个函数，所以在最坏的情况下，该算法需要八倍于不使用三线性插值NDT的时间。然而，在参考扫描仅包含平面的情况下，因为表面没有占据周围所有的网格，使用插值的3D-NDT对每个点需要进行四次函数评估。在大多数使用真实世界扫描数据的情况下，使用插值的3D-NDT所花费的时间实际上是没有使用插值时的四倍左右，因为扫描点通常取自或多或少平坦的表面，而不是稠密地分布在三维空间中。