机器人运动学参数标定

知乎参考: https://www.zhihu.com/question/54682285/answer/336365316

---

1. 机器人正运动学

1.1 机器人DH参数简介

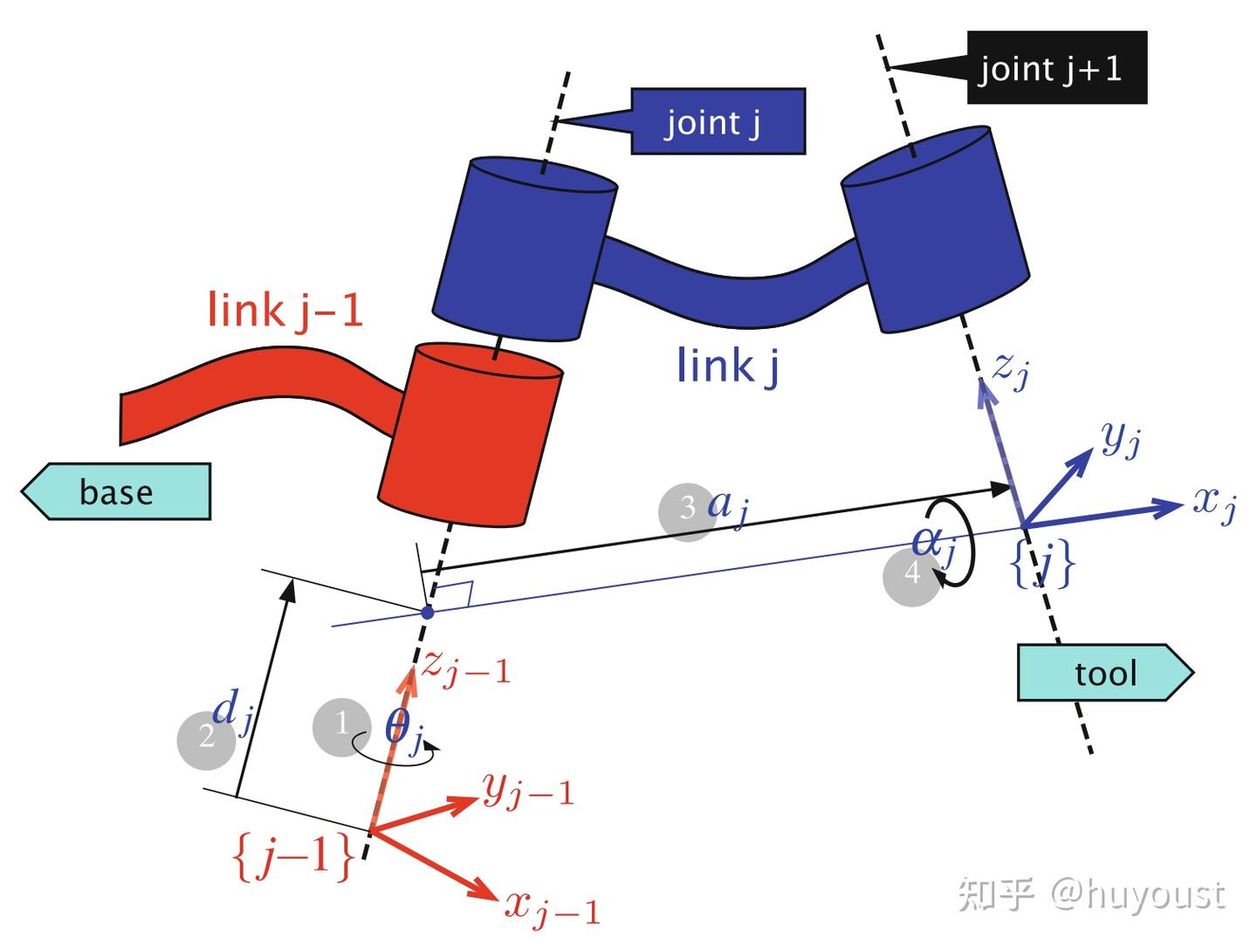
Denavit-Hartenberg（DH）参数是一种标准化方法，用于描述机器人各关节之间的几何关系。通过DH参数，可以将机器人关节的旋转和平移统一表示为矩阵变换。

DH参数包括以下四个变量：

$a_i$：相邻关节轴之间的连杆长度。
$d_i$：沿关节轴的偏移量。
${\alpha }_i$：相邻关节轴之间的扭转角。
${\theta }_i$：关节的旋转角度。
对于机器人，关节角度 ${\theta }_i$ 通常由硬件编码器返回的值 $q_i$ 和关节零位偏置 ${\theta }_i^{\text{offset}}$ 组成： $${\theta }_i=q_i+{\theta }_i^{\text{offset}}$$

1.2 正运动学公式

通过DH参数和关节角度，可以计算机器人末端在基坐标系下的位姿矩阵： $${}_E^B\text{T}=f(\overrightarrow{q},\overrightarrow{\varphi })$$

其中：

$\overrightarrow{q}$：关节角度向量，由编码器返回的值组成。
$\overrightarrow{\varphi }$：机器人运动学参数向量，包括所有的DH参数： $$\overrightarrow{\varphi }=(a_0,d_0,{\alpha }_1,{\theta }_1,\dots ,a_{n-1},d_{n-1},{\alpha }_n,{\theta }_n{)}^T$$

由于装配误差、加工误差等原因，$\overrightarrow{\varphi }$ 中的参数可能存在偏差，因此需要通过标定来修正这些参数。

2. 机器人标定公式

2.1 标定目标

标定的目标是通过实验数据优化 $\overrightarrow{\varphi }$，使得机器人末端的实际位置与理论计算位置之间的误差最小。

2.2 标定方法

标定的核心思想是利用固定的针尖基准点 $P$，通过最小二乘法迭代优化 $\overrightarrow{\varphi }$。

2.2.1 数据采集

• 将机器人末端与针尖基准点 $P$ 对齐。
• 选取若干个不同的关节角度配置 $\overrightarrow{q}$，记录每个配置下的关节角度数据。
• 通过正运动学公式计算每个配置下的末端位姿 ${}_{\text{E}}^{\text{B}}T$。

2.2.2 误差定义

由于末端点始终与针尖基准点 $P$ 接触，末端点在 $P$ 坐标系下的位置应为 $(0,0,0{)}^T$。因此，误差函数可以定义为：
$${\Delta }_E^P\overrightarrow{p}=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]-{}_E^P\overrightarrow{p}$$

其中：

${}_E^P\overrightarrow{p}$：末端点在 $P$ 坐标系下的位置，由正运动学计算得到。

2.2.3 雅可比矩阵

误差函数 ${\Delta }_E^P\overrightarrow{p}$ 对运动学参数 $\overrightarrow{\varphi }$ 的偏导数构成雅可比矩阵 $J$： $$J=\left[\begin{array}{cccc}\frac{\partial f}{\partial a_0}& \frac{\partial f}{\partial d_0}& \cdots & \frac{\partial f}{\partial {\theta }_n}\end{array}\right]$$

2.2.4 参数更新

通过最小二乘法，计算运动学参数的修正值 $\Delta \overrightarrow{\varphi }$：
$$\Delta \overrightarrow{\varphi }=(J^{T}J{)}^{-1}{J}^T\cdot {\Delta }_E^P\overrightarrow{p}$$

然后更新运动学参数：
$${\overrightarrow{\varphi }}^{k+1}={\overrightarrow{\varphi }}^k+\Delta \overrightarrow{\varphi }$$

2.2.5 迭代停止条件

重复上述步骤，直到 $\Delta \overrightarrow{\varphi }$ 足够小，即： $$|\Delta \overrightarrow{\varphi }|<ϵ$$

其中 $ϵ$ 是预设的误差阈值。

3. 参考开源仓库

通过其他方法进行运动学参数标定.

• https://github.com/PhilNad/robot-arm-kinematic-calibration

  • 采用基于POE的机器人运动学校准方法，利用轴配置空间和伴随误差模型，基于扭转和正向运动学的指数积(POE)公式。通过迭代最小二乘优化方案，可以找到螺旋轴校正，从而最小化观测值与机器人正向运动学之间的误差。

• https://github.com/neuebot/Kinematic-Calibration

  • 一种基于圆拟合和对偶矢量几何的方法，用于确定串行机械手的经典Denavit-Hartenberg参数。

• https://github.com/cursi36/Kalibrot?tab=readme-ov-file

  • 采用Kalibrot(一种优化算法)解决寻找正确机器人运动学校准的最佳 DH 参数的问题。