如何更好的理解连续小波变换系数

连续小波变换CWT是一种冗余变换，CWT系数取决于所用的小波，所以理解起来稍微有些困难。为更好地理解CWT系数，本文从简单信号和简单小波开始分析。小波擅长检测信号的不连续性或奇异点，信号的突变点处具有较大的绝对值系数。首先设置一个移位脉冲信号，脉冲发生在第500点的位置。

x = zeros(1000,1);
x(500) = 1;

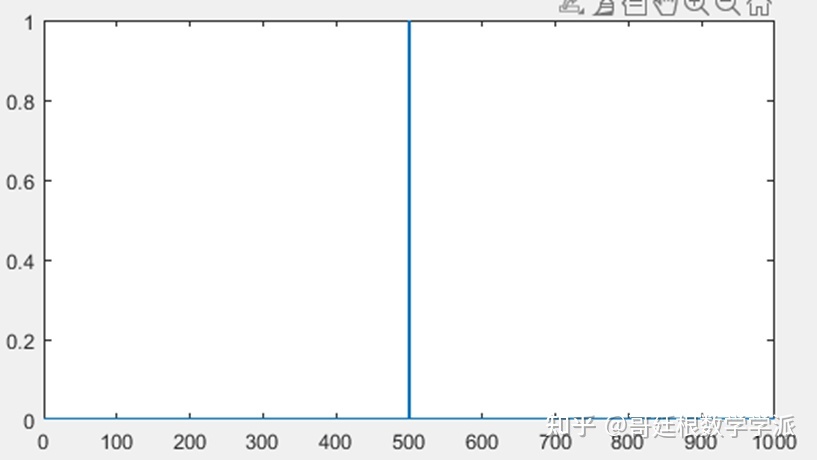
选择了一个简单信号，自然要选择一个简单小波，那自然是haar小波了

在1-128的尺度范围上使用Haar小波计算CWT

CWTcoeffs = cwt(x,1:128,'haar');

CWTcoeffs是一个大小为128×1000的矩阵，矩阵的每一行都包含一个尺度的 CWT系数。由于CWT的尺度为1:128，因此共128 行，矩阵的列维度与输入信号的长度相同。

看一下CWT的时间-尺度谱

cwt(x,1:128,'haar','plot'); 
colormap jet; colorbar;