信号处理——连续小波变换

最新推荐文章于 2024-12-29 21:38:36 发布
最新推荐文章于 2024-12-29 21:38:36 发布
阅读量2.4k 收藏 52
点赞数 20
文章标签： 信号处理
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/ynn4818172/article/details/143663604
版权

1、概括

小波变换是信号时频分析中浓墨重彩的一笔。关于小波变换怎么简单、易懂向大家介绍，我也看了相关博文。目前，我根据公众号出发的理念，带大家浅浅入门一下小波变换，会用即可，深入挖掘理论，请参考专业的论文。

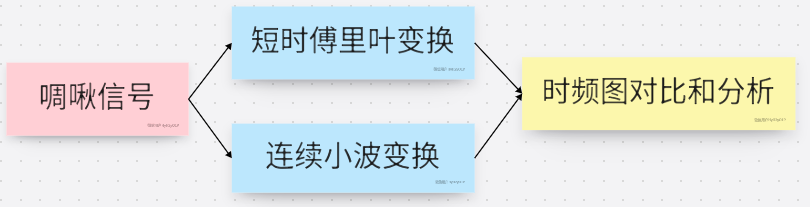
这次给大家带来的是连续小波变换（Continuous Wavelet Transform，CWT），对比短时傅里叶变换(STFT)，CWT有更多的优势、更加灵活。区别于短时傅里叶变换的正弦基函数，连续小波变换采用小波基函数，通过调整小波基函数的尺度因子和时间平移因子，能分析信号在不同频率尺度和时间位置上特性。

本文的流程如下图所示，模拟了一个啁啾信号（一个线性调频信号），并借助matlab的连续小波变换函数cwt，分析了其时频特性，绘制了时频图，对比了短时傅里叶变换的结果，来表明两个方法之间的优劣。

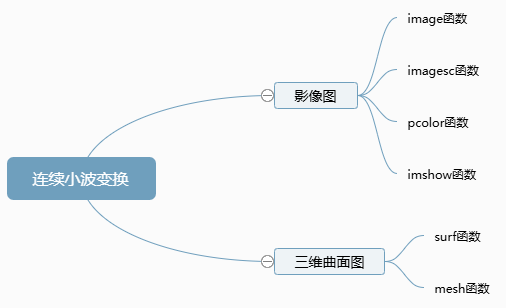
同时，使用matlab的mesh函数、surf函数、imagesc函数、image函数、pcolor函数和imshow函数分别绘制了连续小波变换的时频图，说明不同函数之间的差异，方便大家日后作图时选择合理的绘图函数。

该内容主要参考了一些资料：

https://ww2.mathworks.cn/help/wavelet/ref/cwt.html?searchHighlight=cwt&s_tid=srchtitle_support_results_1_cwt

此外还有MATLAB关于mesh函数、surf函数、imagesc函数、image函数、pcolor函数和imshow函数的说明文档！

代码采用了Matlab 2024a进行运行，欢迎大家测试和提出问题！

2、具体案例

采用短时傅里叶变换中的啁啾信号为例，啁啾(zhōu jiū，英文中为chirp)信号一般是指调频信号，即随着时间的变化，信号的主频在不断发生变化（或增加、或减少）。当这种信号当做音频输出时，听起来会像鸟的唧唧声，所以叫啁啾。

利用matlab的chirp函数生成了一个1s内从100Hz到5000Hz的线性调频信号（啁啾信号），采样频率为24000Hz，具体如下：

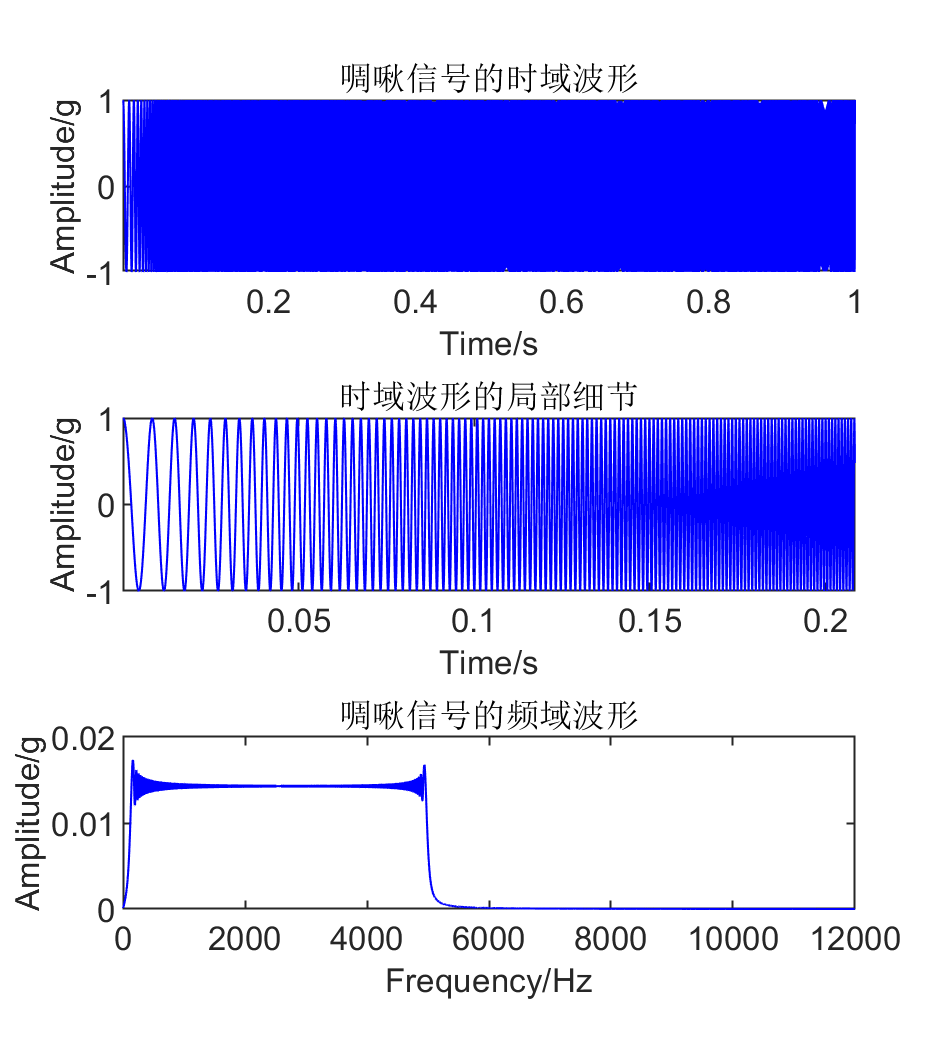
从啁啾信号的局部细节图能发现，随着时间的增长，信号波形越来越密集，即信号的频率逐渐增大。在啁啾信号频谱中，低频占据信号的主频，无法发现信号频率的时变特征。

采用连续小波变换（MATLAB中cwt函数，本文采用的morse小波，其他参数均采用cwt的默认设置），获得啁啾信号的时频分析结果，如下图所示：

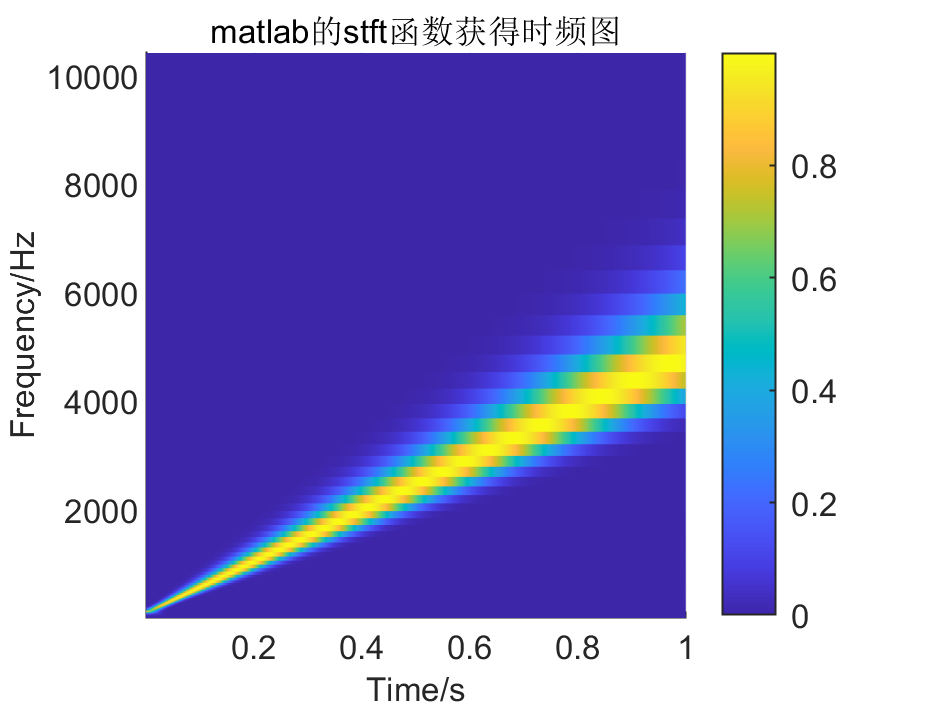
从上图中能发现，啁啾信号的频率从100Hz到5000Hz线性增长，这表明CWT能较好地分析该啁啾信号，对比FFT的结果，表明了CWT在信号时频分析方面的优势。

此外，在上图中CWT所表征的啁啾信号随着时间的增长，其频域的主频带宽越来越大，这似乎与啁啾信号的真实频域状态（主频的带宽不变，主频随时间线性增加）不符，这主要是因为CWT选择的小波尺度并不是最佳的。在CWT中

最低0.47元/天 解锁文章
信号处理基础：信号的时域和频域分析_（24）.小波变换
2401_87715305的博客
03-03 1059
Wfab∫−∞∞ft1aψt−badtWf​ab∫−∞∞​fta​1​ψat−b​dtftf(t)ft是待分析的信号。aaa是尺度参数，表示小波函数的伸缩程度。bbb是位置参数，表示小波函数在时间轴上的平移。ψt\psi(t)ψt是母小波函数，用于生成不同尺度和位置的小波函数。
信号处理算法：小波变换_（1）.小波变换基础理论
最新发布
2401_87715305的博客
03-07 644
小波变换是一种时间-频率分析工具，用于分析非平稳信号。与傅里叶变换不同，小波变换可以同时在时间和频率域中提供信号的局部化信息，这使得它在处理非平稳信号时具有独特的优势。小波变换的基本原理是通过一系列小波基函数对信号进行多尺度分析，从而提取信号在不同尺度下的特征。
图像压缩——小波变换（Wavelet Transform）从连续小波变换谈到离散小波变换
ChuanjieZhu
11-30 3万+
为什么会出先小波变换 窗口傅立叶变换（短时傅立叶变换）虽然可以部分定位时间，但由于窗口大小是固定的，只适用于频率波动小的平稳信号，不适用于频率波动大的非平稳信号。而小波变换可以根据频率的高低自动调节窗口大小，是一种自适应的时频分析方法，可以进行多分辨率分析。 从连续小波变换说起 连续小波变换（Continuous Wavelet Transform，CWT）的定义如下：
连续小波变换的matlab实现
06-03
matlab实现连续小波变换，仅供参考，互相学习
【信号处理】连续小波变换和逆波（Matlab实现）
你的Matlab小助手
06-22 614
它能够将信号在时间和频率上进行局部化的分解，提供了关于信号在不同时间和频率尺度上的详细信息。通过选择合适的小波基函数，连续小波变换可以将复杂的信号分解为不同尺度和位置的小波系数，从而揭示信号中隐藏的特征和模式。这种时频分析的能力使得它在处理非平稳信号、突变信号以及具有时变特性的信号方面具有独特的优势。连续小波变换和逆变换在众多领域都有广泛的应用，如信号处理、图像处理、地震学、语音识别、金融数据分析等，帮助研究人员深入理解和处理各种类型的数据。我就是那艘领航的船，带你乘风破浪，驶向代码的彼岸。
连续小波变换的matlab程序
01-08
连续小波变换的matlab程序，有3种外推方法：零外推，周期外推，镜像外推。在matlab2012上可以运行。
matlab z变换离散化_连续小波变换实现方法的总结及其程序详解
weixin_39936388的博客
10-22 1504
在帖子“给大家分享我自己编的程序-连续小波变换” 中，pengzk版友给出了morlet小波变换的源代码，但其中的许多参数和语句意义不够明确，这就给一些希望了解连续小波变换实现方法的版友带来不便。因此，本帖将对连续小波变换的实现原理做个小结，希望对各位有所帮助。首先说明的是，在Matlab的小波工具箱和pengzk版友提供的程序中，连续小波变换都是依据以下原理实现的：连续小波变换可以看成...
知乎转载 小波变换
u011094358的博客
11-26 4906
著作权归作者所有。 商业转载请联系作者获得授权，非商业转载请注明出处。 作者：咚懂咚懂咚 链接：http://www.zhihu.com/question/22864189/answer/40772083 来源：知乎 从傅里叶变换到小波变换，并不是一个完全抽象的东西，完全可以讲得很形象。小波变换有着明确的物理意义，如果我们从它的提出时所面对的问题看起，可以整理出非常清晰的思路。
Matlab信号处理：连续小波变换
2401_88845856的博客
11-11 4688
小波变换是信号时频分析中浓墨重彩的一笔，本文将介绍连续小波变换（Continuous Wavelet Transform，CWT），对比短时傅里叶变换(STFT)，CWT有更多的优势、更加灵活。区别于短时傅里叶变换的正弦基函数，连续小波变换采用小波基函数，通过调整小波基函数的尺度因子和时间平移因子，能分析信号在不同频率尺度和时间位置上特性。
KAN网络最新优化改进——基于小波变换的KAN网络
hasakie的博客
12-29 1978
KAN网络（Kolmogorov-Arnold Networks）是一种革命性的神经网络架构，源于Kolmogorov-Arnold表示定理。。KAN的核心创新在于将传统神经网络中的固定激活函数替换为可学习的单变量函数，通常以样条函数形式参数化。这种设计不仅提高了模型的灵活性，还显著减少了参数数量，同时增强了可解释性。KAN网络的独特之处在于其能够有效克服高维数据建模中的“维度诅咒”问题，为复杂函数的精确近似提供了一种新的解决方案。
matlab时频分析之连续小波变换cwt
热门推荐
hyhhyh21的博客
04-28 14万+
matlab时频分析之连续小波变换cwt
matlab开发-连续小波变换
08-22
matlab开发-连续小波变换。连续小波变换（CWT）和逆CWT用于重构原始信号。
matlab 连续小波变换和逆变换
05-30
function Xrec = invcwt(wvcfs, mother, scale, param, k) % Xrec = INVCWT(wvcfs, mother, scale, param,k) %uses the Farge 1992 method of using delta functions to reconstruct %waveform. %WAVELET 1D Wavelet transform with optional singificance testing %
小波变换 matlab程序
09-05
小波变换的图像处理%MATLAB2维小波变换经典程序 % FWT_DB.M; % 此示意程序用DWT实现二维小波变换 % 编程时间2004-4-10，编程人沙威 %%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%% clear; clc; T=256; % 图像维数 SUB_T=T/2; % 子图维数 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % 1.调原始图像矩阵 load wbarb; % 下载图像 f=X; % 原始图像 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % 2.进行二维小波分解 l=wfilters('db10','l'); % db10（消失矩为10)低通分解滤波器冲击响应（长度为20） L=T-length(l); l_zeros=[l,zeros(1,L)]; % 矩阵行数与输入图像一致，为2的整数幂 h=wfilters('db10','h'); % db10（消失矩为10)高通分解滤波器冲击响应（长度为20） h_zeros=[h,zeros(1,L)]; % 矩阵行数与输入图像一致，为2的整数幂 for i=1:T; % 列变换 row(1:SUB_T,i)=dyaddown( ifft( fft(l_zeros).*fft(f(:,i)') ) ).'; % 圆周卷积FFT row(SUB_T+1:T,i)=dyaddown( ifft( fft(h_zeros).*fft(f(:,i)') ) ).'; % 圆周卷积FFT end; for j=1:T; % 行变换 line(j,1:SUB_T)=dyaddown( ifft( fft(l_zeros).*fft(row(j,:)) ) ); % 圆周卷积FFT line(j,SUB_T+1:T)=dyaddown( ifft( fft(h_zeros).*fft(row(j,:)) ) ); % 圆周卷积FFT end; decompose_pic=line; % 分解矩阵 % 图像分为四块 lt_pic=decompose_pic(1:SUB_T,1:SUB_T); % 在矩阵左上方为低频分量--fi(x)*fi(y) rt_pic=decompose_pic(1:SUB_T,SUB_T+1:T); % 矩阵右上为--fi(x)*psi(y) lb_pic=decompose_pic(SUB_T+1:T,1:SUB_T); % 矩阵左下为--psi(x)*fi(y) rb_pic=decompose_pic(SUB_T+1:T,SUB_T+1:T); % 右下方为高频分量--psi(x)*psi(y) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % 3.分解结果显示 figure(1); colormap(map); subplot(2,1,1); image(f); % 原始图像 title('original pic'); subplot(2,1,2); image(abs(decompose_pic)); % 分解后图像 title('decomposed pic'); figure(2); colormap(map); subplot(2,2,1); image(abs(lt_pic)); % 左上方为低频分量--fi(x)*fi(y) title('\Phi(x)*\Phi(y)'); subplot(2,2,2); image(abs(rt_pic)); % 矩阵右上为--fi(x)*psi(y) title('\Phi(x)*\Psi(y)'); subplot(2,2,3); image(abs(lb_pic)); % 矩阵左下为--psi(x)*fi(y) title('\Psi(x)*\Phi(y)'); subplot(2,2,4); image(abs(rb_pic)); % 右下方为高频分量--psi(x)*psi(y) title('\Psi(x)*\Psi(y)'); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % 5.重构源图像及结果显示 % construct_pic=decompose_matrix'*decompose_pic*decompose_matrix; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% l_re=l_zeros(end:-1:1); % 重构低通滤波 l_r=circshift(l_re',1)'; % 位置调整 h_re=h_zeros(end:-1:1); % 重构高通滤波 h_r=circshift(h_re',1)'; % 位置调整 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% top_pic=[lt_pic,rt_pic]; % 图像上半部分 t=0; for i=1:T; % 行插值低频 if (mod(i,2)==0) topll(i,:)=top_pic(t,:); % 偶数行保持 else t=t+1; topll(i,:)=zeros(1,T); % 奇数行为零 end end; for i=1:T; % 列变换 topcl_re(:,i)=ifft( fft(l_r).*fft(topll(:,i)') )'; % 圆周卷积FFT end; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% bottom_pic=[lb_pic,rb_pic]; % 图像下半部分 t=0; for i=1:T; % 行插值高频 if (mod(i,2)==0) bottomlh(i,:)=bottom_pic(t,:); % 偶数行保持 else bottomlh(i,:)=zeros(1,T); % 奇数行为零 t=t+1; end end; for i=1:T; % 列变换 bottomch_re(:,i)=ifft( fft(h_r).*fft(bottomlh(:,i)') )'; % 圆周卷积FFT end; construct1=bottomch_re+topcl_re; % 列变换重构完毕 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% left_pic=construct1(:,1:SUB_T); % 图像左半部分 t=0; for i=1:T; % 列插值低频 if (mod(i,2)==0) leftll(:,i)=left_pic(:,t); % 偶数列保持 else t=t+1; leftll(:,i)=zeros(T,1); % 奇数列为零 end end; for i=1:T; % 行变换 leftcl_re(i,:)=ifft( fft(l_r).*fft(leftll(i,:)) ); % 圆周卷积FFT end; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% right_pic=construct1(:,SUB_T+1:T); % 图像右半部分 t=0; for i=1:T; % 列插值高频 if (mod(i,2)==0) rightlh(:,i)=right_pic(:,t); % 偶数列保持 else rightlh(:,i)=zeros(T,1); % 奇数列为零 t=t+1; end end; for i=1:T; % 行变换 rightch_re(i,:)=ifft( fft(h_r).*fft(rightlh(i,:)) ); % 圆周卷积FFT end; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% construct_pic=rightch_re+leftcl_re; % 重建全部图像 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % 结果显示 figure(3); colormap(map); subplot(2,1,1); image(f); % 源图像显示 title('original pic'); subplot(2,1,2); image(abs(construct_pic)); % 重构源图像显示 title('reconstructed pic'); error=abs(construct_pic-f); % 重构图形与原始图像误值 figure(4); mesh(error); % 误差三维图像 title('absolute error display');
matlab小波变换合集
06-25
matlab小波变换合集
matlab一维连续小波变换程序
10-27
一维连续小波变换的matlab程序。对所给离散信号进行一维连续小波变换，结果以位移-时间图显示
波的时频分析方法——小波变换详解
DuHz的博客
11-06 5761
小波变换作为波的时频分析的重要工具，通过其多分辨率分析和时频局部化的特点，能够有效地分析和处理各种复杂的信号和波动现象。本文详细介绍了小波变换的基本概念、数学基础、常用小波函数、快速算法以及其在信号去噪、特征提取、图像压缩等领域的广泛应用，并通过示例代码展示了小波变换在实际中的具体操作。
matlab小波变换频率确定_matlab小波工具箱实例（三）：基于连续小波变换的时频分析...
weixin_39864373的博客
11-22 2805
本文讲解matlab小波工具箱实例(三)：基于连续小波变换的时频分析。目录如下：链接：https://www.mathworks.com/help/wavelet/ug/cwt-based-time-frequency-analysis.html该实例说明了如何利用连续小波变换(CWT)对信号进行时域和频域联合分析，讨论了如何利用CWT定位信号发生变化的位置，还说明了如何利用逆连续小波变...
Matlab图像处理系列——小波变换
小灰灰的FPGA的博客
01-03 4455
分解的目的是力求构造一个在频率上高度逼近的(L®)^2空间的正交小波基，这些频率分辨率不同的正交小波基相当于带宽各异的带通滤波器。在小波分析中，多分辨率的核心就是Vj，Wj空间的正交归一基φjk(t),k为整数位移，j为分辨率的级数。以线性空间的函数空间为例，设X为一非空集合，若在X中规定了线性运算，即元素的加法和数乘运算，并满足相关的结合律及分配律，则X为一线性空间或向量空间。设ek(t)为一函数序列，X表示ek(t)所有可能的线性组合构成的集合，即X是序列ek(t)做成的线性空间。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值