Frenet坐标系 or Cartesian坐标系？

        在智能驾驶领域，轨迹规划问题可以抽象成在一定约束条件下寻找最优解的问题，优化变量、状态方程和约束条件是决定优化问题求解复杂性的关键要素。坐标系的选择不仅是解决问题首先要考虑的，而且对优化问题形式和复杂性有着至关重要的影响。

        智能驾驶领域中广泛使用的坐标系有Frenet坐标系（sl坐标系）和Cartesian坐标系（xy坐标系），两者最大的区别在于坐标轴是否允许为曲线，Cartesian坐标系即几何中常见的直角坐标系，两条坐标轴是相互正交的直线。而Frenet坐标系允许一条坐标轴为曲线（参考线s），故又称为曲线坐标系。

        从定义上可以直觉得出Frenet坐标系特别适合自动驾驶领域的结论，因为只要将道路的中心线作为参考线，就可以将复杂的道路环境简化为直线隧道模型，图1显示了Cartesian坐标系向Frenet坐标系的转换。

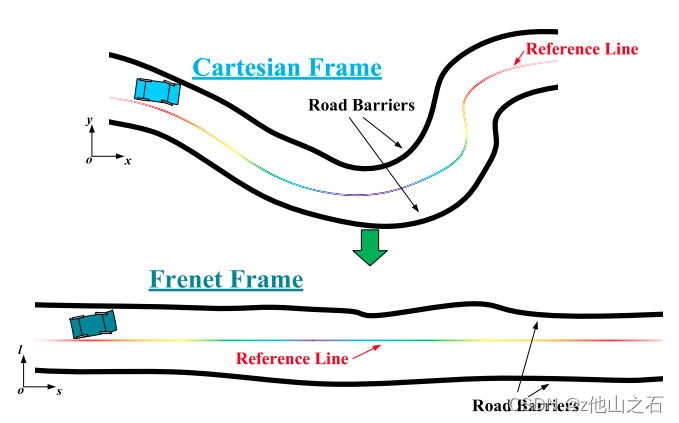
图1 [1]

        将弯曲的道路拉直，这是Frenet坐标系最大（也许是唯一）的优点，怎么评估这个优点的大小？在自动驾驶领域，道路边界是一个不得不处理的约束，很多情况下，非线性的道路边界也是最难处理的约束。这种转换直接将非线性的道路边界约束变成了线性的约束，从而大大简化了后续优化问题的求解。此外，现实中的车辆大多数时候都是沿着道路中心线行驶的，所以在Frenet坐标系中，车辆的运动可以直接解耦为