向量的点乘和叉乘

1. 向量的点乘

定义：

向量点乘又称为内积，结果为标量。

已知空间中的两个向量：a = (x1,y1,z1) , b = (x2,y2,z2) , 则向量a和向量b的内积为：

 

几何意义：

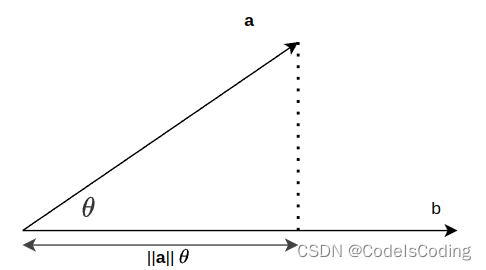
       点乘的结果表示a 在 b 方向上的投影与 ||b|| 的乘积，反映了两个向量在方向上的相似度，结果越大越相似。基于结果可以判断这两个向量是否是同一方向，是否正交垂直，具体对应关系为：

       

        同理，可以内积可以用来计算两个向量之间的夹角：

  

代数性质：

2.向量的叉乘

        定义：叉乘（cross product）又称叉积、外积、向量积（vector product），是对三维度空间中的两个向量的二元运算，使用符号 X。与点积不同，它的运算结果是向量。

已知空间中线性无关的两个向量：a = (x1,y1,z1) , b = (x2,y2,z2) , 则向量a和向量b的外积为：

        其中：   表示 a 和 b 在它们所定义的平面上的夹角（≤≤）。‖a‖ 和 ‖b‖ 是向量  a 和 b  的模长，而 n 则是一个与 a 、b 所构成的平面垂直的单位向量，方向由右手定则决定。根据上述公式，当 a 和 b 平行（即为 0° 或 180°）时，它们的外积为零向量 0。

     

        矩阵表示：

               

 

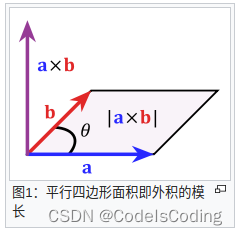
代数性质：