多因子模型（MFM）

看这部分前可以温习下 基本的APT模型
风险的定义

MFM 多因子模型

• 宏观经济因子模型：
• 统计因子模型：
• 基本面因子模型（最有效）：基本面因子模型使用可观察到的股票自身的基本属性，比如分红比
  例、估值水平、成长性、换手率等指标，作为股票市场收益率变动的主要解释变量。基
  本面因子主要是进行横截面分析，确定股票收益率对因子的敏感性(Beta值),基本面
  因子一般可以归纳为基本面类、估值类、市场类。

基本面多因子模型最基本的假设是：具有类似“属性”的股票，在市场上应该有相似的收益
率。这些类似的属性可以是相同的行业、相似的交易属性(比如交易价格、交易量、市值大
小、波动率等)、相似的财务属性(来自于三张财务报表的各种比例或者增长率等)、相似的
估值属性(PB、PE、PS、PCF等)。
多因子模型识别这些共同的基本面因子，并且估计收益率对这些因子的敏感性，得出股票或
者组合的预期收益率，最后通过风险模型，根据投资者的收益—风险偏好挑选合适的股票并
进行权重分配。
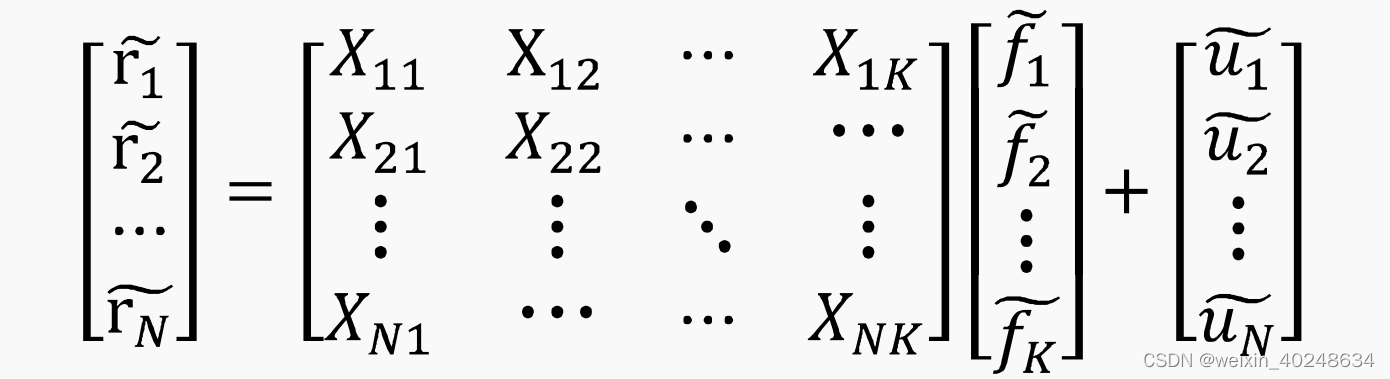
假设一个投资组合由N个股票组成，它们在组合中的权重分别是hpi,hp2,.…,hpN,则组合的
收益率为：

对于一个包含N只股票和K个因子的系统，多因子模型本质上是将对于N只股票的收益一风
险预测转变成对于K个因子的收益—风险预测。对于一个使用多因子模型的投资经理而言，
她/他原本面对的操作对象是N只股票，通过多因子模型，操作对象转换成了K个因子。

多因子模型并不是一个因果关系的模型，即所谓的因子只是在统计上和收益率存在相关关系，
是试图解释收益风险的维度，多因子模型并不关心他们是否存在因果关系。

Alpha的定义和业绩的衡量（IR）：

Alpha定义
Alpha和Beta是相辅相成的，分别是使用线性回归将组合收益率分解为与业绩基准相关的
部分和业绩基准不相关的残差部分。如果rp(t)是投资组合在时点t =1,2,3,…,T上的超额收
益率，rg(t)是业绩基准在同时期的超额收益率，那么回归模型为：

。组合P的残
差收益率是：

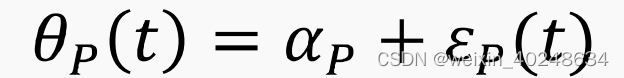
根据定义，业绩基准组合的残差收益率总是等于零，即θg=0总是成立。因此，业绩基准组合的Alpha必然等于零，为了保证αg =0,我们要求股票层面的Alpha列向量满足业绩基准中性的约束。

业绩的衡量 IR：
的业绩衡量指标是信息比率IR(Information Ration),IR是年化残差收益率对年
化残差风险的比值。

多因子模型构建

1. 准备工作

有效因子识别之因子IC值：https://blog.csdn.net/weixin_40248634/article/details/129161702

2. 收益模型

3. 异方差分析：对于模型是否存在异方差的检验，可以采用Breusch-Pagan test或者White test两种方法
4. 多元线性回归
   
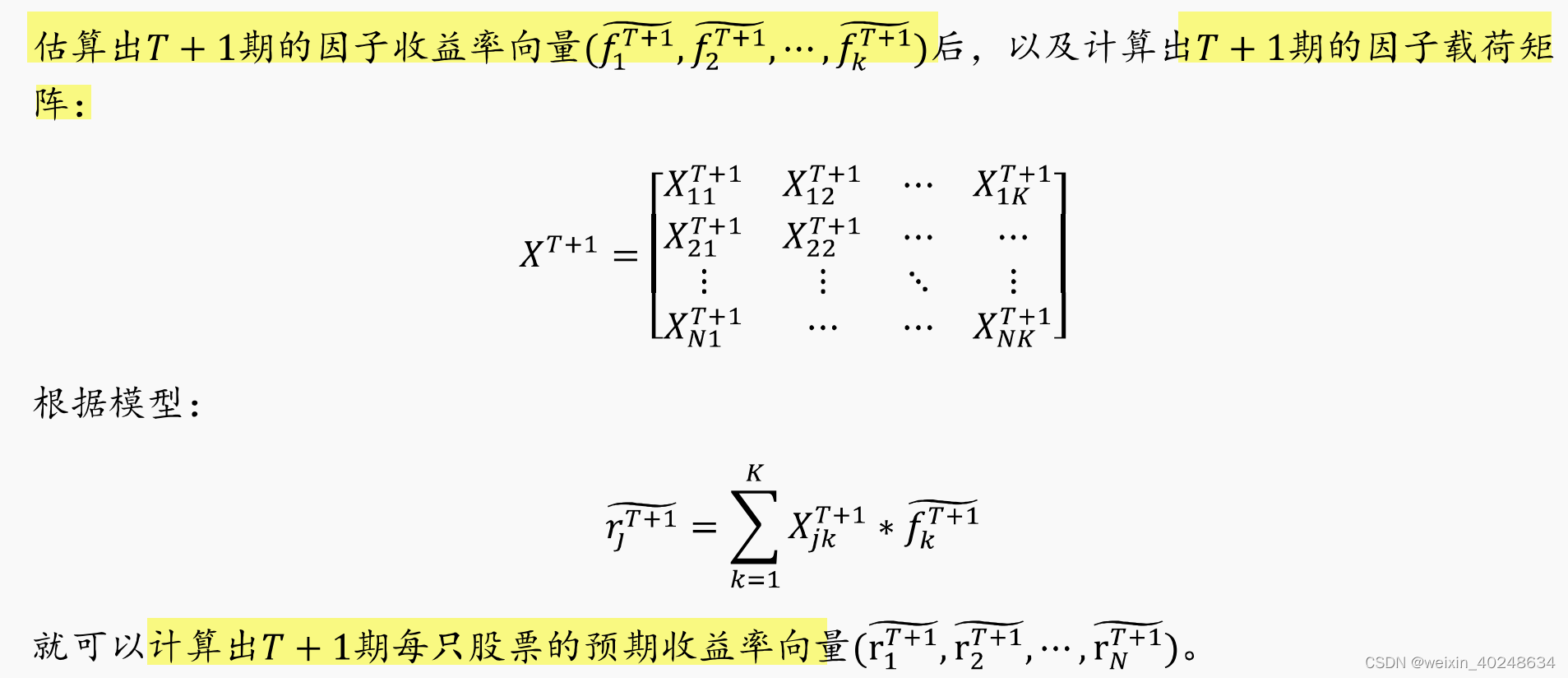
5. 估计因子预期收益:
   目的： 从过去得到的因子收益率（也就是回归的系数）来预测T+1 应该使用的因子收益率，进而才能用于预测T+1 的股价
   
   也可以用指数加权移动平均法(Exponentially Weighted Moving Average,EWMA):时间序列预测法：1 AR(q), MA§, ARMA(q,p) 等。
6. 计算股票预期收益
   

3. 风险模型：

多因子风险模型的主要观点是，股票的收益率可以被一组共同因子和一个仅与该股票有关的
特异因子解释，即任何股票的收益率来自两个方面：共同(因子)部分，特异部分。

多因子模型并不是一个因果关系的模型，即所谓的因子只是在统计上和收
益率存在相关关系，是试图解释收益风险的维度，多因子模型并不关心他们是否存在因果关

在多因子模型的框架下，市场的风险结构变为：

4. 优化模型

投资组合的优化问题 是一个二次优化模型，
要求解的目标是投资组合P的权重向量hp,

1. 第一个模型是控制风险，最大化收益的模型
   
2. 第二个模型是保证收益，最小化风险的模型；

matlab 求解：https://ww2.mathworks.cn/help/optim/ug/quadratic-programming-portfolio-optimization-problem-based.html