01 强化学习——策略梯度法(Policy Gradient PG)（离散动作）

最新推荐文章于 2025-08-21 20:44:37 发布
最新推荐文章于 2025-08-21 20:44:37 发布
阅读量4.1k 收藏 21
点赞数 2
CC 4.0 BY-SA版权
分类专栏： 强化学习 文章标签： 强化学习
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_40493501/article/details/110384894
本文介绍了策略梯度法在强化学习中的定位和作用，详细阐述了策略的参数化表示，特别是针对离散动作的情况。通过数学公式解析了策略梯度的目标、误差和梯度计算，探讨了基线的概念以确保公平性，并提到了在代码实现中采用的损失函数neg_log_prob。

一、来源和定位

1.1 PG算法在强化学习方法中的定位

策略梯度是基于策略搜索方法中最基础的方法，要理解AC，DDPG需要先学习策略梯度。

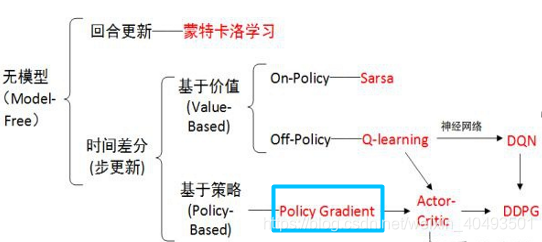
策略梯度方法就是将策略参数化，寻找最优的参数，使总体收益最大。关键在如何将策略参数化。

 

1.2 策略梯度直观理解

策略的表示

一般将策略表示为状态的函数：，

对于离散动作来说是一种随机分布：，随机策略参数化即为参数化这种分布。

对于连续动作来说是随机高斯策略，用高斯策略来表示这种分布，参数化的方法为参数化高斯分布的均值和方差。

策略梯度是将智能体的策略转换成参数的非线性函数，通过寻优参数找到函数的最值，从而使回报值最大。如下图所示，假设有三条路径（每一条路径理解为一个策略\tau）回报分别为1,3，-1.最直观的做法是尽量选择第二条路径，即增加该策略的概率，使最终的回报最大。

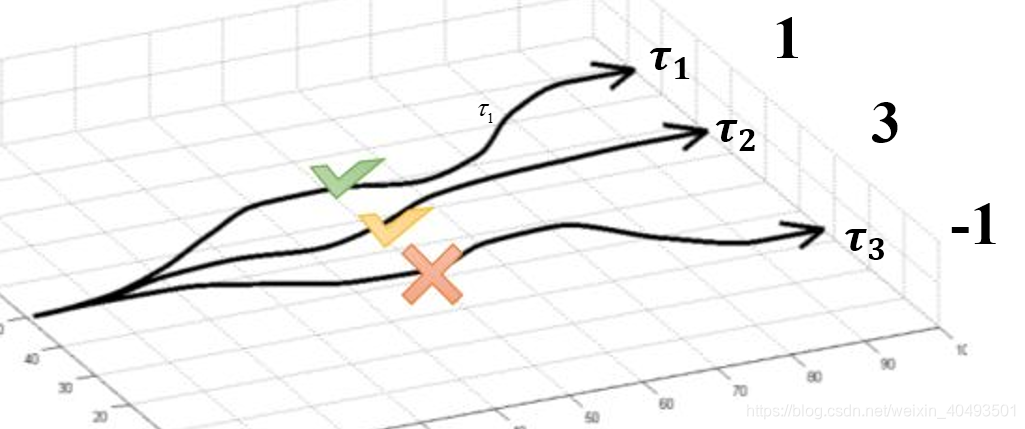
二、问题数学表示

2.1 误差

主要思想是使最终的回报最大，即一个完成的交互episode（从初始状态到最终状态的一个策略\tau）。

目标：【一条完整的episode的回报期望最大】

要使该目标最大，则参数\theta的更新方向为梯度上升的方向。

此公式中有两点需要注意，第一是上式第三行的变换\begin{array}{l} \nabla f(x)= \quad f(x) \nabla \log f(x) \end{array}，该方法在梯度中经常使用，直接记住即可，第二是最后一等式的变换，p(\tau)是概率，与累加和可以看成是求后面部分的期望

策略\tau产生的轨迹如下：

最低0.47元/天 解锁文章

200万优质内容无限畅学
强化学习算法：策略梯度 (Policy Gradient) 原理与代码实例讲解
欢迎来到我的CSDN空间！这里聚焦AI大模型应用实战，分享前沿技术、实战案例与开发经验。
11-29 1045
强化学习算法：策略梯度 (Policy Gradient) 原理与代码实例讲解 关键词：强化学习,策略梯度,策略优化,计算图,深度强化学习,梯度爬坡 1. 背景介绍
一文搞懂策略梯度（Policy gradient）算法（二）
qq_41262334的博客
04-22 2427
在上文中，我们主要介绍了PG算法的目标函数以及策略梯度。可知，在PG算法中，用∇Jθt​的近似来更新策略网络参数θ，从而增大目标函数。在策略梯度计算公式的最后推导中，我们得到策略梯度∇Jθt​的无偏估计同时，留下了一个尾巴——如何得到动作价值函数Qπ​？为了解决这个问题，本文将分别介绍算法和算法，并进一步得到改进版的带基线的策略梯度算法，即以及。
PG（梯度策略算法）
xiao_kong_long的博客
11-11 157
【强化学习】策略梯度（Policy Gradient，PG）算法
小蜗牛的珍贵百宝箱
01-03 2170
在强化学习中，策略是智能体在给定状态下选择动作的概率分布。策略梯度算法的核心思想是通过对策略函数的梯度进行优化，直接更新策略。目标是通过最大化某种目标函数（通常是期望回报）来找到最优策略。假设我们有一个策略参数化为 ( \pi_\theta(a|s) )，其中 ( \theta ) 是策略的参数（通常是一个神经网络的权重）。策略梯度的目标是最大化期望回报：其中，( R(\tau) ) 是从某个策略 ( \pi_\theta ) 生成的轨迹 ( \tau ) 的回报。
【强化学习】策略梯度算法-REINFORCE
最新发布
weixin_49784378的博客
08-21 751
策略梯度算法通过直接优化策略来最大化期望回报，核心是对目标函数求梯度进行参数更新。REINFORCE是最基础的蒙特卡洛策略梯度算法，利用轨迹采样估计梯度。相比值函数方法（如Q-learning），策略梯度更适合连续动作空间，但样本效率较低。基线技巧通过引入状态价值函数作为基准来减少梯度方差，提升训练稳定性。算法实现包含策略网络输出动作概率分布，并通过回报加权对数概率进行策略更新。实验表明REINFORCE在CartPole等环境能有效学习，但需配合基线等技巧优化性能。
深度强化学习1：策略梯度方法（Policy Gradient）
qq_38888209的博客
08-13 1545
【李宏毅深度强化学习笔记】1、策略梯度方法（Policy Gradient） ...
一文搞懂策略梯度（Policy gradient）算法（一）
热门推荐
qq_41262334的博客
04-16 1万+
在强化学习的过程中，从 Sarsa 到 Q-learning 再到 DQN，本质上都是值函数近似算法。值函数近似算法都是先学习动作价值函数，然后根据估计的动作价值函数选择动作。例如，DQN的神经网络结构可以表示为如下图所示：图中，输入是状态s，输出是每个动作的Q值，即对每个动作的评分，分数越高意味着动作越好。通过对值函数的近似，我们可以知道回报最大的路径，从而指导智能体进行动作的选取。但是，。那么有没有一种可能，我们可以跳过动作价值的评估环节，直接从输入状态，到输出策略呢？
强化学习 策略梯度方法
水野与小太郎的博客
08-30 935
一、策略估计方法 行为控制 到目前为止，几乎所有的方法都是基于动作-价值函数的方法，它们都是先学习动作价值函数，然后再根据估计的动作价值函数选择动作，如果没有动作价值函数的估计，那么策略也将不再存在。 下面会讲直接学习参数化的策略，这里给出一个例子： 如果在上述游戏中，游戏者在灰色格子中难以分辨自己的位置，那么如果基于价值函数的方法会得到如下的策略： 在灰色的格子上要么都是左，要么都是右，这很显然不能拿到金币，但如果直接学习策略函数，你用参数 theta 去估计策略函数pi，让他得到行动的.
强化学习（九）- 策略梯度方法 - 梯度上升，黑箱优化，REINFORCE算法及CartPole实例
Stan_Fu的博客
12-07 4304
在之前介绍的方法中，几乎所有方法都是动作价值方法（action-value Method），通过学习动作价值并基于动作价值来学做动作。如果没有行动价值评估，他们的策略甚至不会存在。但在这个部分我们将考虑学习**参数化策略**的方法，这些方法可以在不考虑价值函数的情况下选择动作。价值函数仍然可以用于学习策略参数，但对于动作选择是不必要的。我们使用$\theta \in\mathbb{R}^{d'}$来表示策略的参数向量。所以使用$\pi(a|s, \theta) = Pr\{A_t = a|S_t = s,
策略梯度（Policy Gradient）算法.zip
08-24
策略梯度（Policy Gradient）算法是强化学习领域中一种重要的模型优化方法，它主要用于解决连续动作空间中的问题。TensorFlow 是一个广泛使用的开源库，它提供了丰富的工具和接口，用于构建和训练各种机器学习模型，...
强化学习 - 策略梯度（Policy Gradient）
weixin_48878618的博客
11-10 638
强化学习常见的方法为基于值函数或者基于策略梯度。值函数：值函数最优时得到，即状态s下，最大行为值函数maxQ(s,a)对应的动作。总结：用值函数Q求解连续空间action，也能用但不好用，所以出现了，策略梯度法。
强化学习（六）——策略梯度
LongXinKou的博客
03-22 1825
文章目录1. 演员、环境和奖励2. 最大化期望奖励 1. 演员、环境和奖励 （1）定义 演员就是一个网络，输入状态，输出动作。 环境就是一个函数，输入状态和动作，输出状态。 环境是基于规则的规则，是确定不变的。 奖励是在某一个状态下采取某个动作能够获得的分数。 环境是一个随机变量（因为状态和环境都是在一定分布下抽样获得的），我们可以计算的是奖励的期望值。 （2）某一个轨迹发生的概率 pθ(τ)=p(s1)pθ(a1∣s1)p(s2∣a1,s1)pθ(a2∣s2)p(s3∣a2,s2)⋯=p(s1)∏t=
策略梯度方法：直接优化策略的强化学习技术
AI天才研究院
02-24 1024
1.背景介绍 强化学习是一种机器学习方法，它通过让智能体在环境中进行试错学习，以最大化某种长期奖励。在强化学习中，策略梯度方法是一种重要的优化策略的技术。它直接优化策略，而不是像值迭代或Q学习那样间接优化。这种方法的优点是可以处理连续动作和高维状态空间，而且可以自然地处理随机策略。 2.核心概念与联系
强化学习第四章和第五章
qq_43684686的博客
10-29 889
强化学习第四章和第五章 Policy Gradient 策略梯度 一场游戏 episode(回合) 或者 trial(试验) total reward retun 回报 Trajectory 状态和行为的集合 gradient ascent 梯度下降法 Discounted Return (折扣回报) ...
强化学习EasyRL学习笔记（四）、策略梯度方法
qq_43621439的博客
01-06 433
Easy RL是由清华大学、北京大学以及中国科学院大学的三名硕士生编写的一门强化学习入门书籍，又称为“蘑菇书”Easy RL github地址。笔者主要从事博弈论、多智能体强化学习等方面的研究。最近在学习该本书，故将学习笔记和心得在这里记录下来，供大家观看交流。之后笔者也会继续更新有关多智能体和强化学习的内容，包括强化学习算法原理和代码实现、论文复现、强化学习竞赛等，对文章内容有任何问题或想一起学习强化学习相关内容可以邮件联系。
【强化学习】强化学习数学基础：策略梯度方法(Policy Function Approximation)
小哲的博客
03-13 1241
策略梯度方法是一种强化学习算法，用于寻找最优策略。其思想是直接优化策略参数，使其最大化长期奖励。该方法使用梯度下降来更新策略参数，通过采样一组动作序列，计算出每个动作对应的概率，然后利用梯度信息来调整这些概率，使得累积奖励更高。策略梯度方法具有良好的收敛性和可扩展性，并且在处理高维状态和连续动作空间等实际问题上具有很好的适用性，因此得到了广泛的应用。
【强化学习】策略梯度算法（Policy Gradient）
chy的博客
07-13 2212
基于价值的强化学习算法是根据当前的状态，计算采取每个动作的价值，然后根据价值贪心的选择动作。强化学习中另一个很重要的算法——Policy Gradient则省略中间的步骤，即直接根据当前的状态来输出动作或动作的概率。
【强化学习】策略梯度算法
xingxinbg的博客
10-14 277
基于策略的方法则是存在一个显式的目标策略（使该策略下的动作价值函数期望最大），通过神经网络从每次和环境交互的数据中不断逼近该策略，即神经网络是对策略进行建模，输入是状态，输出是动作的概率分布。Q-learning、DQN都是基于动作价值函数的更新来推导最优策略的，即每次更新并不存在一个显示的策略，这个策略是随着Q值的更新而更新的，这是基于价值的方法。
策略梯度方法
m0_67403773的博客
01-20 1040
策略梯度算法基于价值和基于策略的算法各有什么优缺点？简单易用：通常只需要学习一个值函数，往往收敛性也会更好。保守更新：更新策略通常是隐式的，通过更新价值函数来间接地改变策略，这使得学习可能更加稳定。受限于离散动作；可能存在多个等价最优策略：当存在多个等效的最优策略时，基于价值的方法可能会在它们之间不停地切换。基于策略的算法的优点有：直接优化策略：由于这些算法直接操作在策略上，所以它们可能更容易找到更好的策略；适用于连续动作空间；更高效的探索：通过调整策略的随机性，基于策略的方法可能会有更高效的探索策略。
Keras下的REINFORCE算法实现：策略梯度学习入门
### 策略梯度（Policy Gradient） 策略梯度算法是一种通过直接优化策略来提升模型性能的方法。在强化学习中，策略梯度方法的核心思想是学习一个映射，即从状态到动作的概率分布的映射。策略梯度方法可以解决动作...
评论 7
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值