1. 离散时间鞅(速览)
前情提要
- 鞅的定义及例子
- Doob下鞅分解:下鞅=鞅+可料增过程
- 鞅与停时(Doob停止定理,鞅的离散停时序列是鞅 → \rightarrow →鞅有关停时的等价命题)
- 鞅的矩估计
- 下鞅极值的终值控制不等式(Doob极大值不等式)
- 平方变差过程(平方变差过程的性质【 M 2 − [ M ] M^2-[M] M2−[M]是鞅】、鞅与其平方变差的范数(【能量等式】、【BDG不等式】)、鞅变换的平方变差)
- 鞅的收敛定理(下鞅收敛定理【几乎必然收敛】、鞅收敛定理【 L 1 L^1 L1收敛】)
1. 鞅的定义
- 适应过程与可料过程

- 鞅的定义:实值可积、适应、鞅性

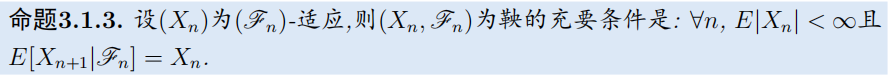
- 举例:

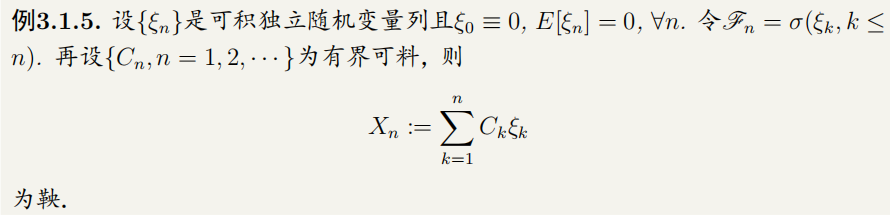

此处 Y n Y_n Yn称为鞅变换。
2. Doob分解:下鞅=鞅+可料增过程
- Doob分解:下鞅=鞅+可料增过程
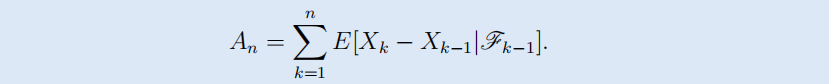

- Doob分解得到的增过程必须要求可料,否则分解不唯一。而对于连续样本轨道的连续时间鞅是唯一的。
3. 鞅与停时(Doob停止定理)
3.1 停止过程
- 停时的定义

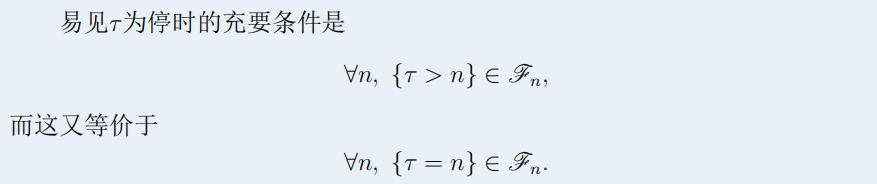
- 停止过程的定义

- 定理3.3.2(Doob停止定理):鞅的停止过程是鞅
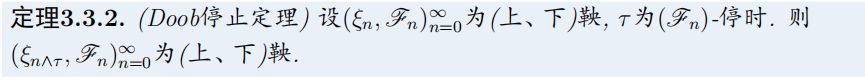

3.2 停止 σ \sigma σ代数
- 停止
σ
\sigma
σ代数的定义
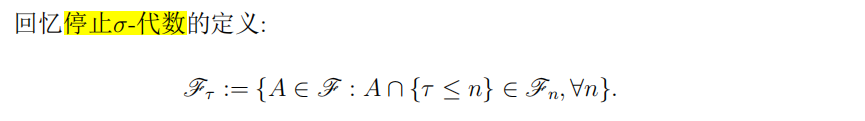
- 停止
σ
\sigma
σ代数的性质:在
{
τ
=
n
}
\{\tau=n\}
{τ=n}时,
F
τ
\mathscr{F}_\tau
Fτ可视为
F
n
\mathscr{F}_n
Fn

3.3 停止过程与停止 σ \sigma σ代数
-
定理3.3.5(Doob停止定理等价命题):鞅的停止过程是鞅
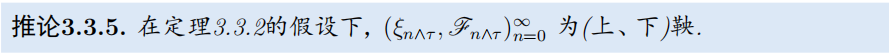

-
定理3.3.8:鞅的离散停时序列是鞅

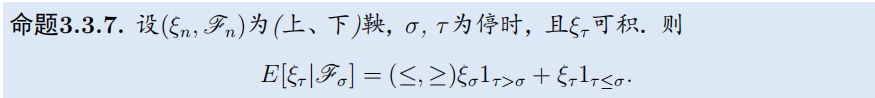

-
定理3.3.8的推论(鞅有关停时的等价命题):这一定理的特殊情况是: 考虑两个有界停时 τ ≤ σ \tau \leq \sigma τ≤σ, 则 E [ ξ σ ∣ F τ ] = ( ≤ , ≥ ) ξ τ E\left[\xi_{\sigma} \mid \mathscr{F}_{\tau}\right]=(\leq, \geq) \xi_{\tau} E[ξσ∣Fτ]=(≤,≥)ξτ, 因此更有
E [ ξ σ ] = ( ≤ , ≥ ) E [ ξ τ ] E\left[\xi_{\sigma}\right]=(\leq, \geq) E\left[\xi_{\tau}\right] E[ξσ]=(≤,≥)E[ξτ]

4. 下鞅极值的终值控制不等式(Doob极大值不等式)
- Kolmogorov-Doob不等式

- Doob极大值不等式
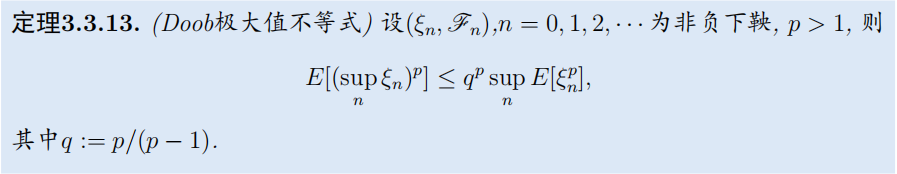
5. 平方变差过程(鞅与其平方变差的范数)
- 平方可积鞅

- 平方变差过程(定义以及性质【鞅的平方-平方变差过程=鞅】)


5.1 鞅&平方变差 范数
- 2范数(能量等式):鞅以及其平方变差的
L
2
L^2
L2范数相同
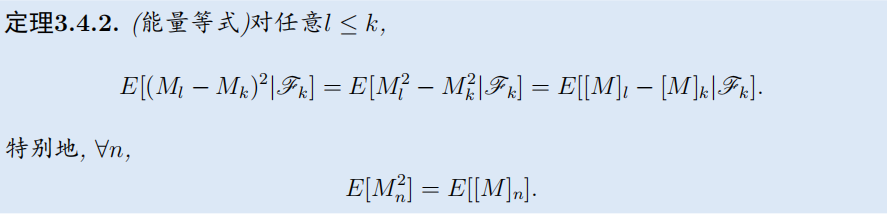
证明:由下鞅的Doob分解 M n 2 = 2 ∑ k = 1 n M k − 1 ( M k − M k − 1 ) + [ M ] n M_{n}^{2}=2 \sum_{k=1}^{n} M_{k-1}\left(M_{k}-M_{k-1}\right)+[M]_{n} Mn2=2∑k=1nMk−1(Mk−Mk−1)+[M]n可得。 - p范数(BDG不等式)

-
- 常数
C
p
C_p
Cp的具体值:
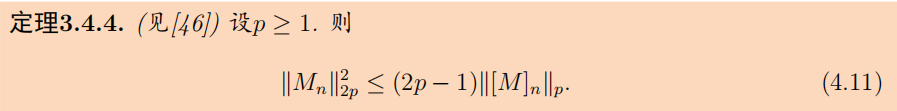
- 常数
C
p
C_p
Cp的具体值:
-
- BDG不等式的推论:


- BDG不等式的推论:
- p范数(d维鞅的BDG不等式) Khintchine不等式的推论
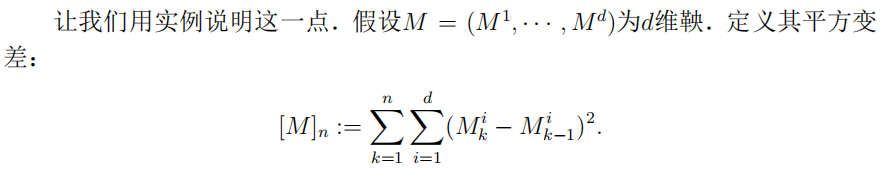

5.2 鞅变换的平方变差
- 鞅变换的定义

- 定理3.4.9 鞅变换的平方变差

6. 鞅的收敛定理
6.1 下鞅收敛定理(几乎必然)
Cauchy准则的内涵: 一个数列收敛的条件是它的项越来越靠近。即它的振幅越来越小:对任意预先给定的数, 振幅超过这个数的项只有有限对.
对任意 a < b a < b a<b, 令 n 1 : = inf { n : λ n ≤ a } , m 1 : = inf { n > n 1 : λ n ≥ n_{1}:=\inf \left\{n: \lambda_{n} \leq a\right\}, m_{1}:=\inf \left\{n>n_{1}: \lambda_{n} \geq\right. n1:=inf{n:λn≤a},m1:=inf{n>n1:λn≥ b } , ⋯ , n k : = inf { n > m k − 1 : λ n ≤ a } , m k : = inf { n > n k : λ n ≥ b } , ⋯ b\}, \cdots, n_{k}:=\inf \left\{n>m_{k-1}: \lambda_{n} \leq a\right\}, m_{k}:=\inf \left\{n>n_{k}: \lambda_{n} \geq b\right\}, \cdots b},⋯,nk:=inf{n>mk−1:λn≤a},mk:=inf{n>nk:λn≥b},⋯. 将 平面上的点 ( n 1 , λ n 1 ) \left(n_{1}, \lambda_{n_{1}}\right) (n1,λn1) 与 ( m 1 , λ m 1 ) \left(m_{1}, \lambda_{m_{1}}\right) (m1,λm1) 用直线连接, ⋯ , ( n k , λ n k ) \cdots,\left(n_{k}, \lambda_{n_{k}}\right) ⋯,(nk,λnk) 与 ( m k , λ m k ) \left(m_{k}, \lambda_{m_{k}}\right) (mk,λmk) 用直线连接, 则每一条这样的直线都从下到上穿越区间 ( a , b ) (a, b) (a,b)。把这些直线的总条数称为 ( λ n ) \left(\lambda_{n}\right) (λn) 对 ( a , b ) (a, b) (a,b)的上穿数.
Cauchy准则: ( λ n ) \left(\lambda_{n}\right) (λn) 收敛(允许收敛到无穷大)的充分必要条件是它对任意区间的上穿数都是有限的.
- 下鞅的Doob上穿不等式
设 ( ξ n ) , n = 0 , 1 , ⋯ , N \left(\xi_{n}\right), n=0,1, \cdots, N (ξn),n=0,1,⋯,N, 是下鞅, a < b a < b a<b. 令
τ 1 : = inf { n : ξ n ≤ a } σ 1 : = inf { n > τ 1 : ξ n ≥ b } ⋯ τ k : = inf { n > σ k − 1 : ξ n ≤ a } σ k : = inf { n > τ k : ξ n ≥ b } ⋯ \begin{gathered} \tau_{1}:=\inf \left\{n: \xi_{n} \leq a\right\} \\ \sigma_{1}:=\inf \left\{n>\tau_{1}: \xi_{n} \geq b\right\} \\ \cdots \\ \tau_{k}:=\inf \left\{n>\sigma_{k-1}: \xi_{n} \leq a\right\} \\ \sigma_{k}:=\inf \left\{n>\tau_{k}: \xi_{n} \geq b\right\} \\ \cdots \end{gathered} τ1:=inf{n:ξn≤a}σ1:=inf{n>τ1:ξn≥b}⋯τk:=inf{n>σk−1:ξn≤a}σk:=inf{n>τk:ξn≥b}⋯
( inf { ∅ } = N ) (\inf \{\emptyset\}=N) (inf{∅}=N). 再令 β ( a , b ) \beta(a, b) β(a,b) 表示 ( ξ n ) \left(\xi_{n}\right) (ξn) 对 ( a , b ) (a, b) (a,b) 的上穿数. 则有

现在考虑无限项的下鞅 ( ξ n , F n ) , n = 0 , 1 , 2 , ⋯ \left(\xi_{n}, \mathscr{F}_{n}\right), n=0,1,2, \cdots (ξn,Fn),n=0,1,2,⋯ 。 以 ( a , b ) (a, b) (a,b) 表示整个序列上 穿 ( a , b ) (a, b) (a,b) 的次数而以 β N ( a , b ) \beta_{N}(a, b) βN(a,b) 表示前 N N N 项上穿 ( a , b ) (a, b) (a,b) 的次数. 则
β N ( a , b ) ↑ β ( a , b ) . \beta_{N}(a, b) \uparrow \beta(a, b) . βN(a,b)↑β(a,b).
于是由上一定理和Fatou引理得到
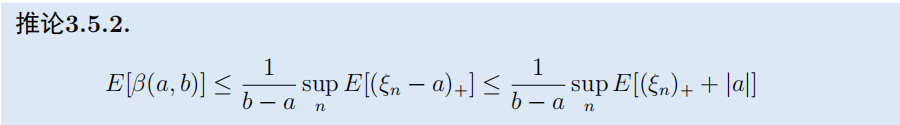
- 下鞅收敛定理:下鞅
sup
n
E
[
∣
ξ
n
∣
]
<
∞
\sup _{n} E\left[\left|\xi_{n}\right|\right]<\infty
supnE[∣ξn∣]<∞,则几乎必然收敛且极限可积


6.2 鞅收敛定理( L 1 L^1 L1收敛)
记 ξ ∞ : = l i m n E [ ξ ∣ F n ] \xi_{\infty}:=lim_nE[\xi|\mathscr{F}_n] ξ∞:=limnE[ξ∣Fn]
若 ξ \xi ξ 为可积随机变量, { F n } \left\{\mathscr{F}_{n}\right\} {Fn} 为 σ \sigma σ 代数流, 则 ξ n : = E [ ξ ∣ F n ] \xi_{n}:=E\left[\xi \mid \mathscr{F}_{n}\right] ξn:=E[ξ∣Fn]为鞅且一致可积(见测度与概率教程P133), 故更有 sup n E [ ∣ ξ n ∣ ] < ∞ \sup _{n} E\left[\left|\xi_{n}\right|\right]<\infty supnE[∣ξn∣]<∞. 这样首先由上一定理得到 ξ ∞ : = lim n → ∞ ξ n \xi_{\infty}:=\lim _{n \rightarrow \infty} \xi_{n} ξ∞:=limn→∞ξn 几乎必然存在, 然后由一致可积性知道 lim n → ∞ E [ ∣ ξ n − ξ ∞ ∣ ] = 0 \lim _{n \rightarrow \infty} E\left[\left|\xi_{n}-\xi_{\infty}\right|\right]=0 limn→∞E[∣ξn−ξ∞∣]=0. (几乎处处收敛且 L 1 L^1 L1收敛)
- E [ ξ ∣ F n ] E[\xi|\mathscr{F}_n] E[ξ∣Fn]是鞅且一致可积;
- 一致可积鞅极限 ξ ∞ \xi_{\infty} ξ∞存在(几乎处处且 L 1 L^1 L1收敛);
-
ξ
∞
\xi_{\infty}
ξ∞ 和
ξ
\xi
ξ 是什么关系?
ξ ∞ : = l i m n E [ ξ ∣ F n ] \xi_{\infty}:=lim_nE[\xi|\mathscr{F}_n] ξ∞:=limnE[ξ∣Fn]= E [ ξ ∣ F ∞ ] E[\xi|\mathscr{F}_\infty] E[ξ∣F∞]
- ξ n \xi_n ξn是鞅,则一致可积<->存在 ξ ∞ \xi_\infty ξ∞,使得 ξ n = E [ ξ ∞ ∣ F n ] \xi_n=E[\xi_\infty|\mathscr{F}_n] ξn=E[ξ∞∣Fn]
- 一致可积鞅极限 ξ ∞ \xi_{\infty} ξ∞存在(几乎必然且 L 1 L^1 L1收敛);
- ξ n \xi_n ξn是鞅,且存在 ξ ∞ \xi_\infty ξ∞,使得 ξ n = E [ ξ ∞ ∣ F n ] \xi_n=E[\xi_\infty|\mathscr{F}_n] ξn=E[ξ∞∣Fn], ξ n \xi_n ξn几乎必然且 L 1 L^1 L1收敛于 ξ ∞ \xi_{\infty} ξ∞。
注释:由6.1节可得 sup n E [ ∣ ξ n ∣ ] < ∞ \sup _{n} E\left[\left|\xi_{n}\right|\right]<\infty supnE[∣ξn∣]<∞, 永远会存在一个 ξ ∞ \xi_{\infty} ξ∞ 使得 ξ n → ξ ∞ \xi_{n} \rightarrow \xi_{\infty} ξn→ξ∞ a.s… 但与此同时有没有 ∥ ξ n − ξ ∞ ∥ 1 → 0 \left\|\xi_{n}-\xi_{\infty}\right\|_{1} \rightarrow 0 ∥ξn−ξ∞∥1→0 则要看 ξ ∞ \xi_{\infty} ξ∞ 是否是该鞅的终端值, 而这又要看它是否一致可积.
























 33
33











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










