强化学习

 

强化学习是从直接的实验中进行学习。Reinforcement learning is learning from direct experiments.

The goal of the learner is to find out the optimal behavior or actions to maximize the reward or the cost function。

---

强化学习中，由于一阶马尔可夫链的限制，agent有时会对相同的状态有相同的表述，并且期望损失会重复计算，学术上称为感知混叠。（perceptual aliasing）解决方案可以是，采取比较多的过去信息，或者是加入注意力agent，在进行观测时，进行一定的选择。

A more concrete definition of learning agents：

马尔可夫决策过程（MDP）是强化学习的基础数学模型。

 

马尔可夫决策过程采用动态规划可以较好的解决。但是，动态规划依赖于精确的模型。而强化学习的出发点是不需要精确的模型的。因此，从动态规划过渡到强化学习一种有效的方法是蒙特卡洛仿真。蒙特卡洛仿真实际上是代替了动态规划。

 

 

 

Conventional method: TD(λ)，一阶时间差分算法。

 

时间差分方法是给定策略条件下，计算期望成本的一种方法。Although it can be used for the learning of action policies through the use of model-based iterative versions of the Policy Iteration algorithm, we would like to have a computational method for a direct model-free learning of optimal actions.

 

Q learning：是一种动作策略（action policy）学习迭代方法，并且给出了一种新的动作价值测度Q值：

 

理解：首先是对一个函数求期望，期望所针对的概率是什么？目前猜测是转移概率。函数是什么？有（1）给定当前状态和动作产生的奖励值：（2）给定下一步状态的最优的成本值，并加上一个折扣。表明：当前的reward和接下来状态的最小成本作为Q值。第二项就是一个期望，对未来一个状态的成本期望。但是这里V*是全局最优的cost value函数，意味着

是最优的策略。因此更进一步的，利用Bellman等式进行展开：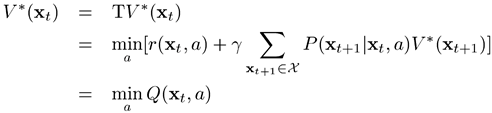

 

这个等式表明，给定当前状态，全局最优的cost value函数为当前状态的最小化Q值。

因此，结合Bellman不等式，可以总结出Q-learning的学习规则：

Q值有一个非常重好的性质：他们是策略无关的或者是策略独立的，因此最优的动作optimal action能够被给出：

可以发现，Q-learning其实都在利用最优的策略。因为最大化Q值，就是在寻找最优的策略。

 

 

其中

Q-learning在学习过程中，实际上要对每一种状态求一个加权和，也就是期望。如果没种状态的转移概率都是相等的，那么即是找出转移到下一个Q值最大的状态。这就是一个学习或者是训练的过程。Q-learning是一种tabular learning，收敛相对较慢。

V值对应的是长期的价值判断，而奖励对应的是短期的瞬时的感受。类比࿱