DC-SLAM：连续离散平滑和建图

---

摘要

原文：原文
代码：代码
摘要：我们提出了一种通用方法，用于在机器人应用中常见的离散-连续因子图中进行最大后验概率（MAP）推理。目前，虽然已经存在一些工具可以灵活且易用地指定和求解基于离散或连续图形模型的推理问题，但尚无类似工具能够处理混合离散-连续问题的通用功能。我们旨在解决这个问题。具体来说，我们提供了一个名为DC-SAM的库，扩展了现有的用于推理问题的工具，将因子图的概念引入离散-连续模型设置中。我们工作的一个关键贡献是提出了一种新颖的求解器，能够有效地恢复离散-连续推理问题的近似解。我们方法的核心思想在于，尽管对包含离散和连续变量的图形模型进行联合推理通常较为困难，许多常见的离散-连续问题可以自然地划分为“离散部分”和“连续部分”，并可以分别独立地轻松求解。利用这种结构，我们以交替的方式优化离散变量和连续变量。因此，我们提出的方法可以实现离散-连续图形模型的简洁表示与近似推理。我们还提供了一种方法，用于近似离散变量和连续变量估计值的不确定性。我们通过将该方法应用于不同的机器人感知应用证明了其通用性，包括鲁棒位姿图优化和基于物体的地图构建与定位。

图 1. 机器人领域的离散-连续因子图

因子图建模了多个与机器人感知相关的离散-连续问题。离散变量节点用红色表示，连续变量节点用蓝色表示，因子节点用黑色表示。

1. 切换系统 (Switching systems)：离散状态控制一个连续过程的演化。
2. 异常值剔除 (Outlier rejection)：离散的内点/外点变量控制是否应该在估计连续变量时使用一部分不可信的测量值。
3. 点云配准 (Point-cloud registration)：离散变量表示对应关系，连续变量表示从源点云到目标点云的相对变换。

1. 简介

概率图模型已成为机器人感知应用中占主导地位的表示范式，广泛应用于一系列重要的估计问题。这种形式化方法促进了包括GTSAM在内的众多算法和软件库的发展，这些库提供了灵活和模块化的语言，用于在这些模型（通常以因子图的形式）中指定和解决推理问题。在与机器人应用相关的模型中，离散-连续图模型捕获了机器人感知、任务和运动规划中出现的关键问题的广泛实例，例如数据关联、异常点拒绝，以及语义同时定位与建图（SLAM）。尽管这些模型很重要，但目前针对特定问题实例的离散-连续图模型方法尚未提出，也没有类似于其纯离散或纯连续模型对手的现成工具来处理混合问题。这正是本文中我们研究的问题。我们的关键见解是，在许多实例中，尽管包含离散和连续变量的图模型的最大后验（MAP）推断很难，但如果固定离散或连续变量，则另一组变量的局部优化会变得容易。连续优化可以通过平滑的基于梯度的方法执行，而离散优化可以通过对连续变量的固定分配，利用标准的最大乘积变量消除算法精确地执行。因此，我们的方法可以有效地推断机器人应用中常见的高维非线性模型。此外，该方法自然扩展了机器人应用中的许多所需推理能力，例如增量计算和不确定性估计。

贡献:
从机器人科学的角度来看，通过利用混合因子图的条件独立结构，我们展示了如何有效地执行局部优化。这种方法保证了目标函数的单调改进。从系统的角度来看，我们的离散-连续平滑与建图（DC-SAM）库扩展了现有的GTSAM工具，增加了以下内容：

1. 混合离散-连续因子的显式构造。
2. 一个能够计算离散-连续问题的近似解的新求解器。
3. 一种不依赖于求解器的解决方案，用于近似离散和连续变量的不确定性。
   我们的方法被应用于点云配准、鲁棒位姿图优化以及语义SLAM。对于前者，我们的通用方法自然地恢复了已知解；在语义SLAM中，我们的方法生成了高质量的轨迹和语义地图，并在导航过程中逐步改进。

2. 相关工作

推断离散-连续图模型的问题涉及多个领域，即使在机器人学领域内部也涵盖了多个研究方向。由于本文的重点是在机器人感知应用中，我们主要讨论这些设置中的相关工作。有兴趣的读者可以参考 Dellaert 等人的研究 [7]，了解这些模型在更广泛的机器人学应用中的讨论，以及 Koller 和 Friedman 的研究 [4, 第14章]，了解关于计算复杂性、推断技术和混合模型推断的一些详细文献。最后，尽管我们在与现有方法的关系中讨论了交替最小化方法，但需要注意的是：一致性框架的简单可用性使得实践者能够比较不同的方法，而无需开发适应现有方法的附加架构。
多假设方法 解决混合估计问题的一类方法是通过枚举并修剪解空间中的假设来处理离散状态，这被称为多假设方法。这些方法出现在经典的检测和跟踪问题中 [8]，以及早期的SLAM应用 [9]。MH-iSAM2 [10] 扩展了 iSAM2 [5] 的功能，使其能够处理连续变量的测量可能具有歧义的情况，这可以通过引入离散变量来表示。MH-iSAM2 维护了一棵假设树，可以像 iSAM2 一样增量更新，提升求解器的效率。他们所考虑的歧义类型都可以通过在因子图中表示连续变量都被条件化的因子来表示。这将应用限制在那些单独离散变量可以解耦的场景中。然而，这种方法在问题设置如动态混合模型中会有一定局限性。
混合和非高斯推断 混合模型中的推断在许多设置中被研究过 [13 提供了综述]。之前的研究方法主要集中在特定的模型，例如条件线性高斯模型 [14]，或者尝试以标准技术（例如离散化连续状态空间以形成离散推理问题）能适应的方式去近似更通用的模型。机器人应用中遇到的模型通常是高维的（状态数量可达数千）并且是非高斯的 [3]，因此通常需要快速求解。这排除了将这些技术直接应用于我们在第V部分中探索的问题的可能性。几个现有方法专门针对非高斯推断在机器人感知中的应用，其中许多方法可被视为混合推断技术的适配，满足复杂要求。FastSLAM [15] 是一种基于粒子滤波的 SLAM 方法，适用于非高斯模型。在该方法中，一组表示当前机器人状态的粒子被保留下来，每个粒子独立地从分布中采样。多模态 iSAM（mm-iSAM）[16] 和 NF-iSAM [17] 提供了一种增量方法，用于连续值变量的推断，通过近似推断边际分布。特别是在离散变量被高效边际化的情况下，它们允许连续状态的后验边际快速生成。
我们的重点 相比之下，我们的工作主要关注从局部优化的角度进行MAP估计。尽管我们描述了给定（近似）MAP估计时近似边际的方法，但非高斯推断技术提供的边际的不确定性更为丰富。然而，考虑到这一较为受限的问题设置（以及粗略的边际近似）使我们在计算成本方面受益显著。先前的研究将优化技术用于非高斯模型中的MAP估计问题，例如 [19, 20]，通过对离散变量进行边际化，并使用平滑的局部优化技术解决连续变量问题。然而，它们并未允许对离散状态的显式估计。
现有工具 目前一些现有的求解器能够对可表示为因子图的模型进行优化。Ceres [21] 和 g2o [22] 提供了适用于机器人学应用的非线性最小二乘优化工具，但它们并不适用于混合因子图的推断。例如，在图1中所示，GTSAM [1] 提供了增量非线性最小二乘求解器（例如 iSAM2 [5]）以及表示和解决离散因子图问题的工具；正因如此，我们选择扩展 GTSAM 的功能，使其适应混合离散-连续模型的设置。最终，Caesar.jl [23] 实现了 mm-iSAM [16]，支持图模型的非高斯推断，包括通过边际化消除离散变量以生成专门涉及连续变量的问题。

3. 背景与预备知识

一个因子图可以表示为 G ≜ { V , F , E } G \triangleq \{ \mathcal{V}, \mathcal{F}, \mathcal{E} \} G≜{V,F,E}，其中 $\mathcal{V}$ 是变量节点集合，$\mathcal{F}$ 是因子集合，$\mathcal{E}$ 是图中的边集合，表示函数的分解结构。在我们的设置中，我们的目标是根据给定的观测值集合 $Z$，确定离散变量 $D$ 和连续变量 $C$ 的最可能赋值。

假设每个测量 $z_k$ 独立于其他测量，且只依赖于变量子集 ${\mathcal{V}}_k$，我们可以将后验概率 $p(C,D\mid Z)$ 分解为以下形式：

$$p(C,D\mid Z)\propto \prod _k{f}_k({\mathcal{V}}_k),\text{\hspace{1em}(1)}$$

其中 V k ≜ { v i ∈ V ∣ ( f k , v i ) ∈ E } \mathcal{V}_k \triangleq \{v_i \in \mathcal{V} \mid (f_k, v_i) \in \mathcal{E} \} Vk​≜{vi​∈V∣(fk​,vi​)∈E}。

在此，因子 $f_k$ 可以分为以下三种类型：

• 离散因子 $f_k(D_k)$，
• 连续因子 $f_k(C_k)$，
• 离散-连续因子 $f_k(C_k,D_k)$。

因此，最大后验估计（MAP）问题可以表述为：

$$C^{\ast },D^{\ast }=\underset{C,D}{\mathrm{argmax}}p(C,D\mid Z),$$

等价于最小化负对数似然：

$$C^{\ast },D^{\ast }=\underset{C,D}{\mathrm{argmin}}\sum _k-\log f_k({\mathcal{V}}_k).\text{\hspace{1em}(2)}$$

具体来说，我们可以将离散-连续因子表示为：

$$-\log f_k(C_k,D_k)=\Vert r_k(C_k,D_k){\Vert }_{\Sigma }^2,\text{\hspace{1em}(3)}$$

其中 $r_k:\Omega \times \mathcal{D}\to {\mathbb{R}}^m$ 是关于 $C$ 的一阶可微函数，$\mathcal{D}\subseteq {\mathbb{N}}^{|D|}$。

---

4. 方法概述

本部分描述了解决公式 $(2)$ 的优化方法。

4.1 交替最小化

一般来说，公式 $(2)$ 的 MAP 推断问题是计算上不可行的（参见 [4, Sec. 13.1.1]）。然而，通过固定某一变量集合（例如 $C$ 或 $D$），另一个集合的优化问题可以通过现有方法有效求解。具体来说：

• 若固定 $D$，连续变量 $C$ 的优化可以通过平滑的梯度优化技术（如 [5], [24]）进行。
• 若固定 $C$，离散变量 $D$ 的优化可以通过标准的变量消除技术（如 [4, Sec. 13.2.1]）精确求解。

在最坏情况下，离散变量 $D$ 的优化可能需要指数级的状态数，但在许多实际问题中，最坏情况的复杂度并不会发生。

我们的关键洞察是，利用因子图模型的条件独立性结构，可以开发一种高效的局部优化方法，且该方法保证后验概率的单调改进。

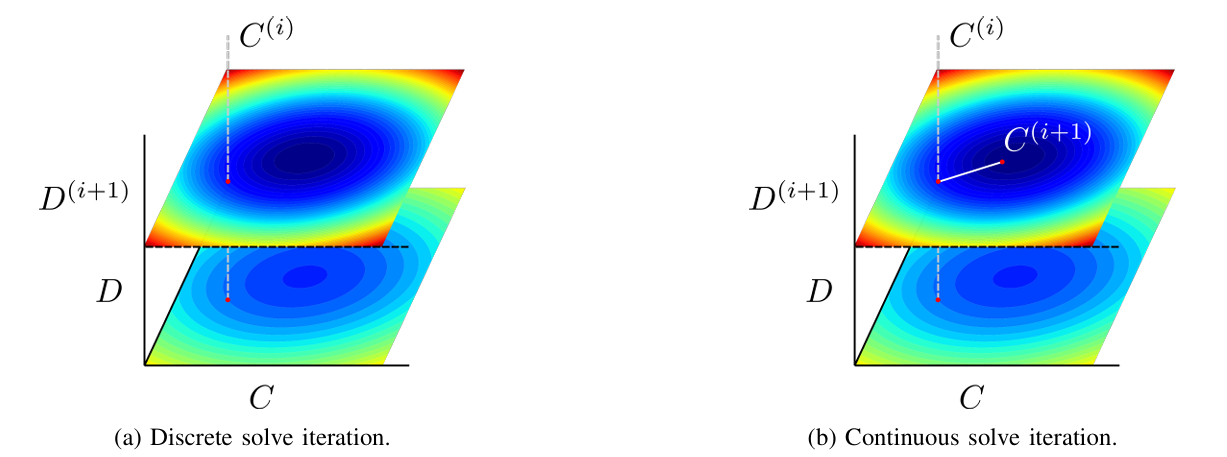
图 2. 单次优化迭代的概述: (a) 首先，给定一个初始迭代 $C^{(i)}$，我们通过最大乘积消除法 (max-product elimination) 精确求解离散变量的最优分配。(b) 接着，基于离散变量的最新分配值，更新连续变量（例如，使用信赖域方法 [24]）。颜色表示解的目标值，从低成本（蓝色）到高成本（红色）。
例如，考虑将离散状态划分为互斥的子集 $D_j\subseteq D$，这些子集在给定连续状态的条件下是条件独立的：

$$p(D\mid C,Z)\propto \prod _{j}p(D_j\mid C,Z).\text{\hspace{1em}(4)}$$

可以很容易地验证，由于每个子集 $D_j$ 是互斥的，在公式 $(4)$ 中优化条件问题可以分解为涉及每个 $D_j$ 的子问题：

$$\underset{D}{\max }p(D\mid C,Z)\propto \prod _j\left[\underset{D_j}{\max }p(D_j\mid C,Z)\right].\text{\hspace{1em}(5)}$$

关键在于，我们将求解最大值的计算从乘积的最大值，变为每个最大值独立计算的乘积。在许多情况下，离散状态可以分解为特别小的子集（$|D_j|\ll |D|$），从而可以高效地执行推理。许多在机器人领域中常见的混合优化问题具有这种有利的条件独立结构。例如，图 1b 和图 1c 所展示的鲁棒位姿图优化与点云配准分别具有这样的形式（公式 (4)），每个子集 $D_j$ 仅包含一个离散变量。此外，一些离散因子图虽然在条件于连续状态后无法如此剧烈地分解，但仍可能允许有效的推理。例如，图 1a 描绘了一个切换系统，在连续变量的条件下，生成的离散图为隐藏马尔科夫模型，在其中最可能的离散状态分配可以通过维特比算法[25] 计算。接下来，我们将利用这些思想构建一种算法，以有效地为公式 (2) 形式的问题生成解。定义负对数后验为：

$$\mathcal{L}(C,D)\triangleq -\log p(C,D\mid Z).\text{\hspace{1em}(6)}$$

根据公式 (2)，联合优化问题可形式化为：

$$C^{\ast },D^{\ast }=\arg \underset{C,D}{\min }\mathcal{L}(C,D).\text{\hspace{1em}(7)}$$

我们的交替最小化方法（如图 2 所示）步骤如下：首先，固定初始迭代 $C^{(i)}$。然后，目标是解决以下子问题：

$$D^{(i+1)}=\arg \underset{D}{\min }\mathcal{L}(C^{(i)},D).\text{\hspace{1em}(8a)}$$

$$C^{(i+1)}=\arg \underset{C}{\min }\mathcal{L}(C,D^{(i+1)}).\text{\hspace{1em}(8b)}$$

我们可以重复公式 (8a) 和 (8b)，直到 $\mathcal{L}(C,D)$ 的相对减少足够小，或者达到最大迭代次数。即使找到这些子问题 (8a) 和 (8b) 的最优解是具有挑战性的，我们的方法也仅需要使其满足以下下降准则即可确保目标函数单调改进：

$$\mathcal{L}(C^{(i)},D^{(i+1)})\le \mathcal{L}(C^{(i)},D^{(i)}),\text{\hspace{1em}(9a)}$$

$$\mathcal{L}(C^{(i+1)},D^{(i+1)})\le \mathcal{L}(C^{(i)},D^{(i+1)}).\text{\hspace{1em}(9b)}$$

方法更新和命题: 有许多方法可以用于更新满足条件 (9a) 和 (9b) 的离散状态和连续状态。对于离散状态，可以通过使用最大乘积算法 (max-product algorithm) 来计算子问题 (8a) 的最优解，从而确保 (9a) 中的下降条件。对于连续状态，(9b) 中的下降条件可以通过使用例如信赖域方法 (trust region method, 例如 [24]) 来细化连续状态以满足目标 (8b)。

因此，我们得到以下命题： 令 $\mathcal{L}(C,D)$ 为需要最小化的目标函数，其初始迭代点为 $C^{(0)},D^{(0)}$。假设在每次迭代中，离散更新满足 (9a) 的下降条件，同时连续更新满足 (9b) 的下降条件。那么，交替优化所得的估计 $C^{(i)},D^{(i)}$ 满足：

$$\mathcal{L}(C^{(0)},D^{(0)})\ge \mathcal{L}(C^{(1)},D^{(1)})\ge \cdots \ge \mathcal{L}(C^{(T)},D^{(T)}),$$

即此过程会单调地优化目标函数。

证明:

固定一个初始迭代点 $(C^{(i)},D^{(i)})$。根据假设，在离散更新后，有：

$$\mathcal{L}(C^{(i)},D^{(i+1)})\le \mathcal{L}(C^{(i)},D^{(i)})\text{\hspace{1em}(从 (9a))}$$

因此，更新后的组合 $(C^{(i)},D^{(i+1)})$ 至少和先前的分配一样好。以相同的推理，进行后续连续更新会产生满足：

$$\mathcal{L}(C^{(i+1)},D^{(i+1)})\le \mathcal{L}(C^{(i)},D^{(i+1)})\text{\hspace{1em}(从 (9b))}$$

结合以上不等式，我们得到：

$$\mathcal{L}(C^{(i+1)},D^{(i+1)})\le \mathcal{L}(C^{(i)},D^{(i+1)})\le \mathcal{L}(C^{(i)},D^{(i)}).$$

上述不等式链对所有 $i$ 都成立，完成证明。

4.2 在线增量推理

许多机器人问题自然具有增量解决方案的特性，其中新信息仅影响我们希望估计的一小部分状态。由于我们的交替最小化方法仅依赖于分别改进离散和连续子问题的能力，因此可以依赖现有技术以增量方式解决这些问题。

具体而言，在连续优化子问题中，我们使用 iSAM2 [5] 将包含连续变量的图重构为一个贝叶斯树，从而允许对连续变量进行增量推理。同样，得益于公式 (4) 中的离散分解，如果引入了新的离散变量且这些变量在给定当前连续状态估计时与所有先前的离散状态条件独立，我们能够无需重新计算以前估计变量的解，直接为这些变量求解最可能的分配。

因此，我们能够有效地解决在线推理问题，如在第 V-C 节中所展示，我们针对在线 SLAM 问题给出了解决方案。

---

4.3 恢复边缘概率

不确定性表示在机器人感知的许多应用中是重要的。DC-SAM 支持离散和连续变量的边缘分布的后验恢复，用于从估计中近似边缘分布。

对于连续变量，我们使用拉普拉斯近似 [26, Sec. 4.4]，此方法被多种非线性最小二乘求解器（例如 Ceres、g2o 和 GTSAM）采用。具体而言，我们针对连续变量固定线性化点（以及对离散变量的当前估计），并围绕该线性化点计算近似的高斯分布中心。

对于离散变量，我们固定对连续变量的分配，并计算在此线性化点条件下离散变量的确切边缘分布。边缘分布的公式如下（参考 [4, Ch. 10]）：

$$p(D_j\mid \hat{C},Z)=\sum _{D_j}p(D\mid \hat{C},Z),D_j\subseteq D,\text{\hspace{1em}(12a)}$$

$$p(C_j\mid \hat{D},Z)={\int }_{C\setminus C_j}p(C\mid \hat{D},Z),C_j\subseteq C.\text{\hspace{1em}(12b)}$$

这一方法的原因是，在一般情况下，由特定（离散-连续）因子图捕获的后验模式数可能呈现组合爆炸的增长。计算精确的边缘概率很可能变得难以处理。相比之下，通过利用公式 (4) 中的条件分解，解决公式 (12a) 中离散变量的边缘问题是可行的。

值得注意的是，我们的边缘恢复方法不需要使用第 IV-A 节中提到的交替最小化策略，只需任何能提供估计值 $\hat{C},\hat{D}$ 的方法即可。

公式 (12b) 中的连续边缘概率是通过使用拉普拉斯近似 [6] 来估计的。在我们的推导中，为了简化讨论，将连续状态作为向量 $C\in {\mathbb{R}}^d$。假设点 $\hat{C}$ 是连续子问题 (8b) 的一个关键点，即 $\nabla \mathcal{L}(C,\hat{D}){\mid }_{\hat{C}}=0$。

我们对目标函数 $\mathcal{L}(C,\hat{D})$ 在点 $\hat{C}$ 周围进行泰勒展开：

$$\mathcal{L}(C,\hat{D})\approx \mathcal{L}(\hat{C},\hat{D})+\frac{1}{2}(C-\hat{C}{)}^{\top }A(C-\hat{C}),\text{\hspace{1em}(13)}$$

其中 $d\times d$ 的海森矩阵 $A$ 定义为：

$$A=-{\nabla }^2\mathcal{L}(C,\hat{D}){\mid }_{\hat{C}}.\text{\hspace{1em}(14)}$$

对公式 (13) 的两边取指数并进行适当的归一化，得到了以下高斯近似形式：

$$p(C\mid \hat{D},Z)\approx \frac{|A{|}^{1/2}}{(2\pi {)}^{d/2}}\exp \left\{-\frac{1}{2}\Vert C-\hat{C}{\Vert }_A^2\right\},\text{\hspace{1em}(15)}$$

其中 $\Vert C-\hat{C}{\Vert }_A^2$ 表示马氏距离范数 $\sqrt{C^{\top }AC}$。

当所有涉及连续变量的因子呈现如下形式时，即 $\mathcal{L}$ 在 $\hat{C}$ 处的局部线性近似带有一个对测量函数 $r$ 的雅可比矩阵的海森矩阵 $A$，我们有 $A⪰0$ [28]。

此外，还可以通过矩阵 $A$ 的平方根（即信息矩阵的平方根）提取一个变量子集 $C_j$ 的边缘概率。