2. Erster Hauptsatz der Thermodynamik
2.1 Energieerhaltung, Energiebilanz
2.2 Arbeit am geschlossenen System
Volumenändergungsarbeit:
W
v
=
−
∫
1
2
p
d
V
W_v=-\int^2_1 pdV
Wv=−∫12pdV
geschlossenes System(reversibel)
zugeführte Arbeit: positiv
abgeführte Arbeit: negativ
Dissipationsenergie:
$ W_{diss}$ ist immer positiv
Die gesamte am geschlossenen System verrichtete Arbeit:
W
g
12
=
W
v
12
+
W
d
i
s
s
12
W_{g12}=W_{v12}+W_{diss12}
Wg12=Wv12+Wdiss12
Für ein geschlossenes System (reversibel) besteht es:
W
g
12
=
−
∫
1
2
p
d
V
+
W
d
i
s
s
12
W_{g12}= -\int ^2_1 pdV + W_{diss12}
Wg12=−∫12pdV+Wdiss12
Nutzarbeit an der Kolbenstange:
$ W_{n12} = W_{v12}-W_{u12}$
2.3 Innere Energie
W
g
12
=
U
2
−
U
1
W_{g12}=U_2-U_1
Wg12=U2−U1
adiabates, geschlossenes System
2.4 Wärme
Wärme ist die Energie, die allein aufgrund eines Temperaturunterschiedes zwischen zwei System oder zwischen einen System und siner Umgebung übertragen wird.
$ Q_{12}+W_{g12}=U_2-U_1$
geschlossenes System
Definition: Wärme ist die Differenz aus der Änderung der inneren Energie und der verrichteten Arbeit, wenn das betrachtete System geschlossen ist.
Q
12
−
∫
1
2
p
d
V
+
W
d
i
s
s
12
=
U
2
−
U
1
Q_{12}-\int^2_1pdV+W_{diss12}=U_2-U_1
Q12−∫12pdV+Wdiss12=U2−U1
gilt allgemein
zugeführte Wärme: positiv
abgeführte Wärme: negativ
2.5 Arbeit am offenen System und Enthalpie
technische Arbeit: W t 12 W_{t12} Wt12
Diese an einem offenen System verrichtete Arbeit nennen wir technische Arbeit.
W
t
12
=
W
t
12
r
e
v
+
W
d
i
s
s
12
W_{t12}=W_{t12}^{rev}+W_{diss12}
Wt12=Wt12rev+Wdiss12
W
t
12
r
e
v
W^{rev}_{t12}
Wt12rev ist der reversible Anteil von der technischen Arbeit.
Enthalpie:

考虑左边有一个Kolben,其上的压强为
p
1
p_1
p1,右边也有一个Kolben其上的压强为
p
2
p_2
p2,我们分析m+M,那么我们可以通过
W
g
12
=
U
2
−
U
1
W_{g12}=U_2-U_1
Wg12=U2−U1得出
W
t
12
+
p
1
V
1
−
p
2
V
2
=
U
2
−
U
1
W_{t12}+p_1V_1-p_2V_2=U_2-U_1
Wt12+p1V1−p2V2=U2−U1进一步化简可得
W
t
12
=
(
U
2
+
p
2
V
2
)
−
(
U
1
+
p
1
V
1
)
W_{t12}=(U_2+p_2V_2)-(U_1+p_1V_1)
Wt12=(U2+p2V2)−(U1+p1V1)
Die Klammerausdrücke enthalten nur Zustandsgrößen, die zu einer neuen Zustandsgröße, der Enthalpie, zusammengefasst werden.
H
=
U
+
p
V
H=U+pV
H=U+pV
Deshalb bekommen wir eine neue Gleichung, die für adiabates und offenes System gilt.
W
t
12
=
H
2
−
H
1
W_{t12}=H_2-H_1
Wt12=H2−H1
Wenn man alle andere Faktoren betrachtet, bekommt man wieder eine andere Gleichung:
W
t
12
∗
=
H
2
−
H
1
+
m
2
(
c
2
2
−
c
1
2
)
+
m
g
(
z
2
−
z
1
)
W_{t12}^*=H_2-H_1+{m\over2}(c^2_2-c^2_1)+mg(z_2-z_1)
Wt12∗=H2−H1+2m(c22−c12)+mg(z2−z1)
oder:
w
t
12
∗
=
h
2
−
h
1
+
1
2
(
c
2
2
−
c
1
2
)
+
g
(
z
2
−
z
1
)
w_{t12}^*=h_2-h_1+{1\over2}(c^2_2-c^2_1)+g(z_2-z_1)
wt12∗=h2−h1+21(c22−c12)+g(z2−z1)
(Den Index * verwenden wir für die technische und die reversible technische Arbeit, wenn die Änderung der kinetischen und potenziellen Energie berücksichtigt wird.)
####Totalenthalpie:
H
∗
=
H
+
m
c
2
2
H^*=H+m{c^2\over2}
H∗=H+m2c2
Sind die Systemgrenzen nichtadiabat, so muss bei der Energiebilanz die an der Systemgrenze übertretende Wärme berücksichtigt werden. Außerdem berücksichtigt man die Änderung der kinetischen und potenziellen Energie, so erhält man.
Q
12
+
W
t
12
∗
=
H
2
−
H
1
+
m
2
(
c
2
2
−
c
1
2
)
+
m
g
(
z
2
−
z
1
)
(1)
Q_{12}+W^*_{t12}=H_2-H_1+{m\over2}(c^2_2-c^2_1)+mg(z_2-z_1) \tag{1}
Q12+Wt12∗=H2−H1+2m(c22−c12)+mg(z2−z1)(1)
offenes System
auf die Masse
m
m
m bezogen
q
12
+
w
t
12
∗
=
h
2
−
h
1
+
1
2
(
c
2
2
−
c
1
2
)
+
g
(
z
2
−
z
1
)
q_{12}+w^*_{t12}=h_2-h_1+{1\over2}(c^2_2-c^2_1)+g(z_2-z_1)
q12+wt12∗=h2−h1+21(c22−c12)+g(z2−z1)
Die technische Arbeit, die nach Gl 1 mit der Enthalpie und der W’rme verknüpft ist, kann auch ohne Kenntnis kalorischer Größen ermittelt werden. Hierzu gehen wir von der differenzierten Gleichung
H
=
U
+
p
V
H=U+pV
H=U+pV aus:
d
H
=
d
U
+
p
d
V
+
V
d
p
dH=dU+pdV+Vdp
dH=dU+pdV+Vdp
d
U
=
d
H
−
p
d
V
−
V
d
p
dU=dH-pdV-Vdp
dU=dH−pdV−Vdp
und führen sie in die differenzierte Gleichung
d
Q
−
p
d
V
+
d
W
d
i
s
s
=
d
U
dQ-pdV+dW_{diss}=dU
dQ−pdV+dWdiss=dUein. Wir erhalten damit eine vom offenen System unabhängige Gleichung:
d
Q
−
p
d
V
+
W
d
i
s
s
=
d
H
−
p
d
V
−
V
d
p
dQ-pdV+W_{diss}=dH-pdV-Vdp
dQ−pdV+Wdiss=dH−pdV−Vdp
d
Q
+
V
d
p
+
d
W
d
i
s
s
=
d
H
dQ+Vdp+dW_{diss}=dH
dQ+Vdp+dWdiss=dH
Q
12
+
∫
1
2
V
d
p
+
W
d
i
s
s
12
=
H
2
−
H
1
Q_{12}+\int^2_1Vdp+W_{diss12}=H_2-H_1
Q12+∫12Vdp+Wdiss12=H2−H1
gilt allgemein
再把公式1代入,我们就可以得出technische Arbeit的公式了。
W
t
12
∗
=
∫
1
2
V
d
p
+
m
2
(
c
2
2
−
c
1
2
)
+
m
g
(
z
2
−
z
1
)
+
W
d
i
s
s
12
W^*_{t12}=\int^2_1Vdp+{m\over2}(c^2_2-c^2_1)+mg(z_2-z_1)+W_{diss12}
Wt12∗=∫12Vdp+2m(c22−c12)+mg(z2−z1)+Wdiss12
Ändern sich kinetische und potenzielle Energie nicht, so ist die reversible technische Arbeit
W
t
12
r
e
v
=
∫
1
2
V
d
p
W^{rev}_{t12}=\int^2_1Vdp
Wt12rev=∫12Vdp
offenes System
Natürlich lässt sich auch für das geschlossene System der Ausdruck
∫
1
2
V
d
p
\int^2_1Vdp
∫12Vdp berechnen, die Bedeutung einer tatsächlich verrichteten Arbeit hat er jedoch nur beim offenen System
Entsprechend gilt, dass
−
∫
1
2
p
d
V
-\int^2_1pdV
−∫12pdV nur beim geschlossenen System die Bedeutung einer wirklich verrichteten Arbeit - der Volumenänderungsarbeit
W
v
12
W_{v12}
Wv12 - hat.
Dagegen behalten die innere Energie
U
U
U und die Enthalpie
H
H
H unabhängig vom System Ihre Bedeutung als Zustandsgröße.
2.6 Formulierungen des ersten Hauptsatzes der Thermodynamik
Die Energie eines abgeschlossenen Systems bleibt stets konstant
Geschlossenes, ruhendes System:
Q
12
+
W
g
12
=
U
2
−
U
1
Q_{12}+W_{g12}=U_2-U_1
Q12+Wg12=U2−U1
Offenes System, stationärer Prozess:
Q
12
+
W
t
12
∗
=
H
2
−
H
1
+
m
2
(
c
2
2
−
c
1
2
)
+
m
g
(
z
2
−
z
1
)
Q_{12}+W^*_{t12}=H_2-H_1+{m\over2}(c^2_2-c^2_1)+mg(z_2-z_1)
Q12+Wt12∗=H2−H1+2m(c22−c12)+mg(z2−z1)
2.7 Kalorische Zustandsgleichungen
2.7.1 Kalorische Zustandsgleichungen eines homogenen Systems
d
u
=
(
∂
u
∂
T
)
v
d
T
+
(
∂
u
∂
v
)
T
d
v
du=({\partial u\over\partial T})_vdT+({\partial u \over \partial v})_Tdv
du=(∂T∂u)vdT+(∂v∂u)Tdv
d
h
=
(
∂
h
∂
T
)
p
d
T
+
(
∂
h
∂
p
)
T
d
p
dh=({\partial h\over\partial T})_pdT+({\partial h \over \partial p})_Tdp
dh=(∂T∂h)pdT+(∂p∂h)Tdp
2.7.2 Spezifische Wärmekapazitäten eines homogenen Systems
Die jeweils ersten Differenzialquotienten in obigen Gleichungen haben für die thermodynamische PRaxis besondere Bedeutung, da sie bei vielen VOrgängen auftreten. Sie werden spezifische Wärmekapazität genannt:
c
v
=
(
∂
u
∂
T
)
v
c_v=({\partial u\over\partial T})_v
cv=(∂T∂u)v
spezifische Wärmekapazität bei konstantem Volumen
c
p
=
(
∂
h
∂
T
)
p
c_p=({\partial h\over\partial T})_p
cp=(∂T∂h)p
spezifische Wärmekapazität bei konstantem Druck
Für ein geschlossenes System haben wir zwei folgenden Gleichungen:
bei
V
=
k
o
n
s
t
a
n
t
V=konstant
V=konstant:
Q
12
+
W
d
i
s
s
12
=
m
∫
1
2
c
v
d
T
Q_{12}+W_{diss12}=m\int^2_1c_vdT
Q12+Wdiss12=m∫12cvdT
bei
p
=
k
o
n
s
t
a
n
t
p=konstant
p=konstant:
Q
12
+
W
d
i
s
s
12
=
m
∫
1
2
c
p
d
T
Q_{12}+W_{diss12}=m\int^2_1c_pdT
Q12+Wdiss12=m∫12cpdT
2.7.3 Kalorische Zustandsgleichungen des idealen Gases
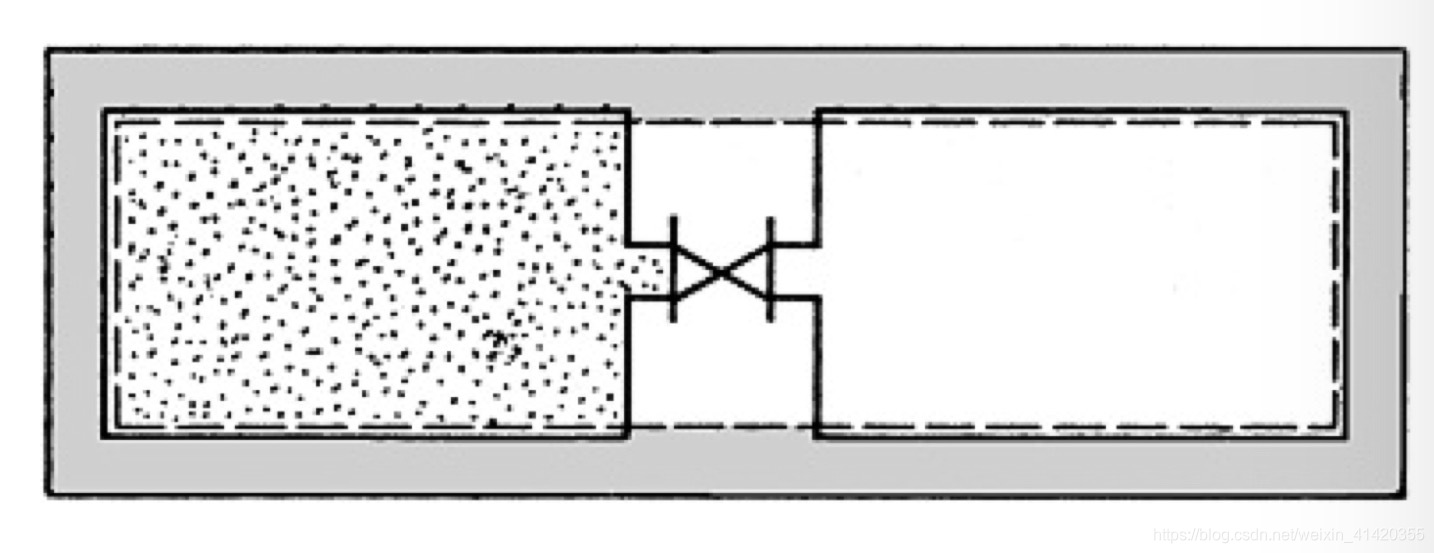
Im linken Gefäß eines wärmedichten Systems befindet sich Gas, das rechte Gefäß steht unter Vakuum. Öffnet man das Ventil, so strömt ein Teil des Gases in das rechte Gefäß über, wobei sich das Gas im linken Gefäß abkühlt und im rechten erwärmt. Nach Ausgleich der Temperatur wird die Ausgangstemperatur beim idealen Gas exakt erreicht, wie durch Temperaturmessungnachweisbar ist, beim nichtidealen Gas stellt sich meist eine Abkühlung ein, bei sehr hohen Temperaturen kann auch eine Erwärmung bobachtet werden.
Die spezifische innere Energie des Systems muss nach dem Überströmen die gleiche wie vorher sein, da Energie in keiner Form die Systemgrenze überschritten hat; das spezifische Volumen hat sich jedoch vergrößert. Demnach ist die innere Energie des idealen Gases bei konstanter Temperatur vom Volumen unabhängig. Die Ableitung der inneren Energie nach dem Volumen
(
∂
u
∂
v
)
T
({\partial u \over\partial v})_T
(∂v∂u)T muss dann gleich null sein.
Deshalb:
d
u
=
(
∂
u
∂
T
)
v
d
T
=
c
v
d
T
(2)
du=({\partial u \over \partial T})_vdT=c_vdT \tag{2}
du=(∂T∂u)vdT=cvdT(2)
Auch die Enthalpie des idealen Gases ist eine reine Temperaturfunktion:
h
=
u
+
p
v
=
u
+
R
i
T
h=u+pv=u+R_iT
h=u+pv=u+RiT
Da
u
u
u eine reine Temperaturfunktion ist, kann auch
h
h
h nur von der Temperatur abhängen und muss somit unabhängig vom Druck sein. Das bedeutet, dass der Ausdruck
(
∂
h
∂
p
)
T
({\partial h \over \partial p})_T
(∂p∂h)T in
Q
12
+
W
d
i
s
s
12
=
m
∫
1
2
c
p
d
T
Q_{12}+W_{diss12}=m\int^2_1c_pdT
Q12+Wdiss12=m∫12cpdT beim idealen Gas gleich null sein muss. Dadurch vereinfacht sich
Q
12
+
W
d
i
s
s
12
=
m
∫
1
2
c
p
d
T
Q_{12}+W_{diss12}=m\int^2_1c_pdT
Q12+Wdiss12=m∫12cpdT mit
(
∂
h
∂
p
)
T
=
c
p
({\partial h \over \partial p})_T=c_p
(∂p∂h)T=cp zu
d
h
=
(
∂
h
∂
T
)
p
d
T
=
c
p
d
T
(3)
dh=({\partial h \over \partial T})_pdT=c_pdT\tag{3}
dh=(∂T∂h)pdT=cpdT(3)
Gl 2 und Gl 3 sind die kalorischen Zustandsgleichungen des idealen Gases.
Der Punkt über dem Formelzeichen zeigt an, dass es sich um Vorgänge innerhalb einer bestimmten Zeit - hier je Stunde - behandelt z. B. um den Massen strom
m
˙
\dot m
m˙ in kg/h,
2.7.4 Spezifische Wärmekapazitäten des idealen Gases
未完待续

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








