贝特朗（Bertrand）悖论

几何概型

抛硬币、掷骰子之类游戏中涉及的概率，是离散的，抛丢结果的数目有限（2或6）。如果硬币或骰子是对称的，每个基本结果发生的概率相等。这种随机事件被称为古典概型。

数学家们将古典概型推广到某些几何问题中，使得随机变量的结果变成了连续的，数目成为了无限多，这种随机事件被称之为“几何概型”。

古典概型向几何概型的推广，类似于有限多个整数向“实数域”的推广。了解几何概型很重要，因为与之相关的“测度”概念（长度、面积等），是现代概率论的基础。

几何概型和古典概型都使用“等概率假设”。然而，只要涉及到无穷大，便经常会产生一些怪异的结果。著名的几何概型悖论是法国数学家贝特朗（Joseph Louis Bertrand，1822–1900）于1889年提出的贝特朗悖论。

贝特朗问题

在一个圆内任意选一条弦，这条弦的弦长长于这个圆的内接等边三角形的边长的概率是多少？

求解方法

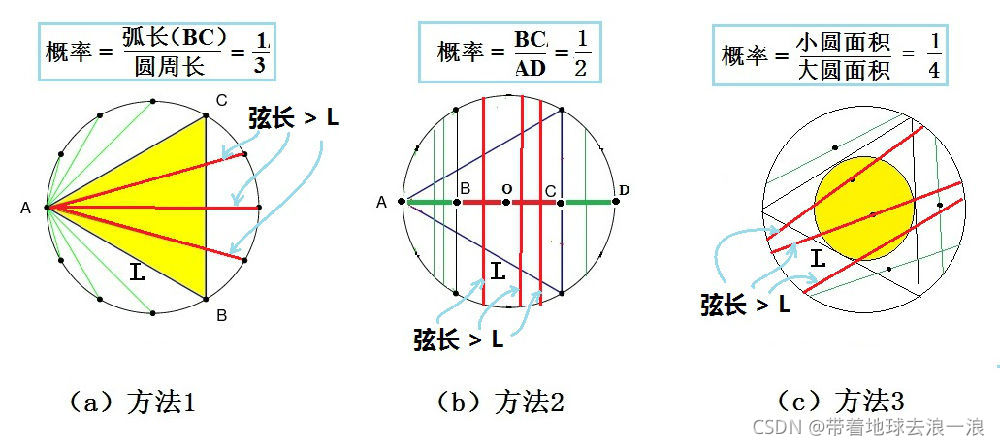
方法1：首先假设弦的一端固定在圆上某一点（比如A），如上图(a)，弦的另一端在圆周上移动。移动端点落在弧BC上的弦，长度均超过圆内接正三角形的边长L，而其余弦的长度都小于L。由于对称性，BC弧长占整个圆周的1/3，所以可得弦长大于L的概率为BC弧长与圆周长之比，即P=1/3。

方法2：首先选择圆的一个直径，比如上图(b)中的AD。过该直径上的任何点作直径的垂线，与圆相交形成弦。从图2b中可以看出：当直径上动点的位置在B和C之间时，所得弦的弦长大于正三角形的边长L，动点位置在BC之外的弦长小于L。因为线段BC的长度是整个直径的一半，所以由此可得弦长大于L的概率为P=1/2。

方法3：如上图(c)所示，作一个半径只有圆的半径的二分之一的同心圆（称为小圆），称原来的圆为“大圆”。考虑大园上任意弦的中点的位置可知：当中点位于小圆内部时，弦长符合大于L的要求。因为小圆的面积是大圆面积的1/4。所以，概率也为P=1/4。

同一问题有三种不同答案，上述的三种解法可以用下图进行更加直观地表示。如果观测弦的中点分布情况，方法1和方法2的中点分布是不均匀的，方法3的中点分布是均匀的。若观测弦的分布情况，方法2的弦会看起来比较均匀，而方法1和方法3的弦则较不均匀。

悖论分析

方法1：由于对称性，可预先固定弦的一端。仅当弦与过此端点的切线的交角在60°～ 120° 之间，其长才合乎要求。所有方向是等可能的（Chord's end points are random），则所求概率为1/3 。此时假定端点在圆周上均匀分布。

方法2：由于对称性，可预先指定弦的方向。作垂直于此方向的直径，只有交直径于1/4 点与 3/4 点间的弦，其长才大于内接正三角形边长。所有交点(弦与圆心的距离)是等可能的（Distance from the center is random），则所求概率为1/2 。此时假定弦的中心在直径上均匀分布。

方法3：弦被其中点位置唯一确定。只有当弦的中点落在半径缩小了一半的同心圆内，其长才合乎要求。中点位置都是等可能的（Point of intersection with a perpendicular is random over the circle）,则所求概率为1/4。此时假定弦长被其中心唯一确定。

之所心对同一问题存在着三种不同答案，究其原因在于圆内“取弦”时规定尚不够具体，不同的“等可能性假定”导致了不同的样本空间。贝特朗悖论引起人们注意，在定义概率时要事先明确指出样本空间是什么。