机器人运动学轨迹规划（一）

对于一个机器人系统，一般都会经历加速、匀速、减速的运动过程。在整个运动过程中，速度随时间的变化曲线称为速度曲线。常见的速度曲线主要有：梯形曲线(T型)、S型曲线(S)、多项式曲线等。

对于一个梯形速度曲线，主要包括匀加速、匀速、匀减速过程。对于S型速度曲线，一般主要包括加加速、匀加速、减加速、匀速、加减速、匀减速、减减速，一共7段，所以一般又称为7段式。

同梯形速度曲线相比，S型速度曲线对电机和传动系统的冲击伤害会更小，但是在相同的最大速度和最大加速度喜爱，S型速度曲线在运动相同的位移下，其时间要更长。

下图一(figure1)和图二(figure2)分别是在运动相同的距离，设定相同的最大速度和最大加速度条件下的梯形速度曲线和S型速度曲线。在本文里，设定最大速度V=50mm/s，最大加速度a=10mm/s2, 运动距离L=500mm, 对于S型速度曲线而言，设定最大加加速度(又称jerk,加速度的导数)aa=4mm/s3。

     

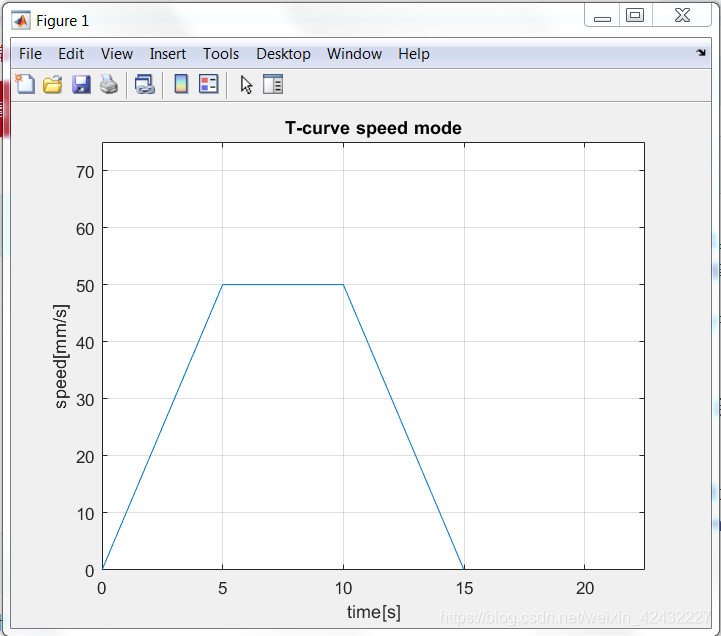
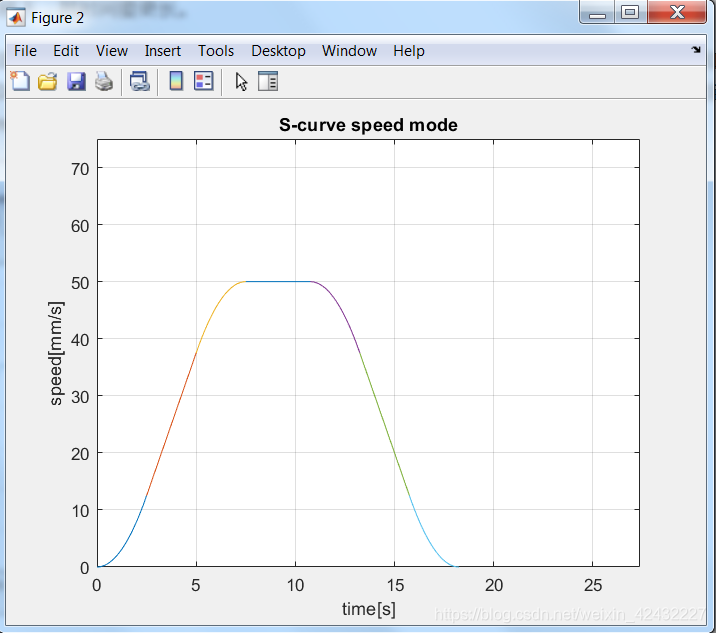
可以看出，figure2运行相同的距离比figure1要长。但正如上文所介绍，梯形曲线相对于S型曲线对电机的冲击要大的多，上面两图的Matlab代码如下：

clc;clear;
%% input parameters
V = 50;    %% max speed
a = 10;     %% max acceleration
L = 500;  %% Distance
aa =4;     %% jerk aa = d(a)/dt    f