凸优化——对偶问题

最新推荐文章于 2025-04-03 15:17:12 发布
最新推荐文章于 2025-04-03 15:17:12 发布
阅读量1.5k 收藏 27
点赞数 9
分类专栏： 数学知识
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_42444577/article/details/102923662
版权
本文深入探讨了凸优化的核心概念，包括拉格朗日函数、对偶函数及其性质，通过实例解析共轭对偶问题，详细阐述了强对偶与弱对偶的概念，以及对偶问题在多目标优化和经济学中的应用。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

凸优化——对偶问题

拉格朗日函数与对偶函数

在这里插入图片描述

inf是极小化的意思
lambda和v是拉格朗日乘子（lambda——和不等式相关的拉格朗日乘子，v——和不等式相关的拉格朗日乘子）

对偶函数性质

在这里插入图片描述

g()<=L()<=p*

对偶函数例子

在这里插入图片描述

得一个关于v的凹函数
在这里插入图片描述
在这里插入图片描述

函数的共轭

在这里插入图片描述

共轭函数一定是一个凸函数

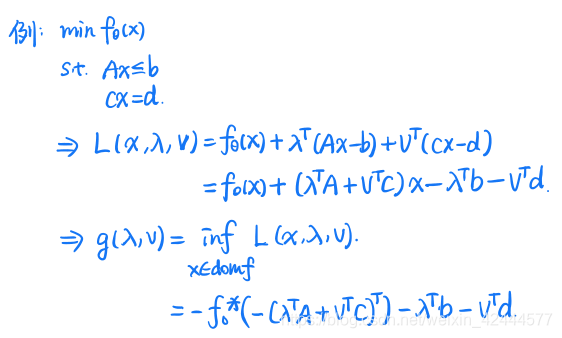
在这里插入图片描述
在这里插入图片描述

将一个拉格朗日对偶函数的一部分用共轭函数来表示

对偶问题

根据对偶函数性质2（如上），可以通过求最优的对偶函数来逼近p*的下界
在这里插入图片描述
在这里插入图片描述

D是对偶问题，P是原问题
对偶问题就是最大化对偶函数，同时lambda大于等于0

强对偶、弱对偶

对偶问题一定是一个凸优化问题

强对偶、弱对偶、对偶间隙

在这里插入图片描述

B（x,r）是以x为中心，r为半径的小球
aff D是D的仿射包
aff D可以理解为D所在的整个空间
Relint D其实就是把D的边界去掉形成的开集

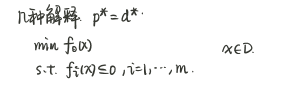
在这里插入图片描述
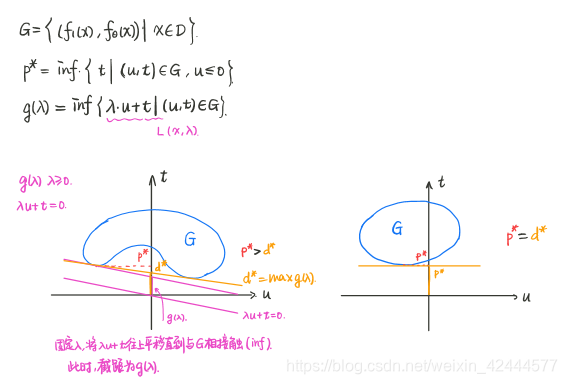
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

p*=d*的几种解释

在这里插入图片描述

几何解释

在这里插入图片描述
在这里插入图片描述

p是u<=0(St条件给定)下的f0(x)的最小值，即可行域下t的最小值
lambdau+t得g（lambda）=在t轴的截距
在给定lambda大于等于0时，lambdau+t=g()的函数是一条直线。在求对偶函数时为了让g()最小，该直线必过下部的切线；在求d时为了让g()最大可以改变斜率lambda

鞍点的解释

在这里插入图片描述

多目标优化的解释

在这里插入图片描述
在这里插入图片描述

经济学解释

在这里插入图片描述

Python实现蒙特卡罗方法求解优化问题——拉格朗日对偶问题
AI天才研究院
09-01 2220
蒙特卡罗（Monte Carlo）方法是近代科学计算中一个重要的算法。它利用随机化的方法来解决问题，可以有效地模拟系统中的各种非线性行为。蒙特卡罗方法在很多领域都有广泛应用。例如，模拟电路的电压波形、建筑结构设计、保险产品的风险评估等。此外，它还被用作信号处理、概率论、生物信息学等诸多方面。而我们今天要介绍的就是蒙特卡罗方法在求解优化问题上的一种应用——拉格朗日对偶问题（Lagrangian dual problem）。
凸优化第五章对偶 5.2Lagrange对偶问题
清风吹斜阳
02-10 1759
5.2Lagrange对偶问题 Larange对偶问题 弱对偶性 强对偶性和slater约束准则 例子 Lagrange对偶问题 对于任意的一组，对偶函数给出了优化问题的最优值的一个下界。从Lagrange函数能够得到的最好下界是什么？ 将此问题转化为优化问题： 上述问题为原问题的Lagrange对偶问题，且是一个凸优化问题，因为是凹函数。如果是Lagrange对偶问题的最优解，...
凸优化与对偶问题
u013421941的博客
01-20 5528
这个是凸优化的最基本的形式： $$\begin{align}&\operatorname{minimize}&&f_0(x)\\&\operatorname{subject\;to}&&f_i(x)\leq0,\quad i=1,\dots,m\\&&&h_i(x)=0,\quad i=1,\dots,p\end{align}$$ 其中f0为目标函数，第二行与第三行均为约束条件。从f0
凸优化－对偶问题
11-15 1951
05 November 2015 1. 引言 凡心所向，素履所往，生如逆旅，一苇以航。 很高兴阿森纳能在欧冠上战胜拜仁，在虎扑上看到这样的一句话，颇有感触，借来作为这篇博文的开始，生活中我们需要一些勇气去追寻自己的理想。回到本篇内容上，对偶是个神奇的东西，从文学角度而言，对偶和对仗属于一种修辞手法，即用字数相等，语义对称的方法来表征想法或抒发情感。“凡心所向，素履所往，生如逆旅，一
凸优化系列-对偶问题
最新发布
科研探索ing！研究方向：人工智能及优化
04-03 1038
本博客主要关注凸优化理论中的对偶问题，从最简单的线性规划的对偶问题开始介绍，然后介绍通用的对偶问题，并且介绍 KKT 条件及其推导过程。最后介绍具体在凸优化理论中应用到的一些对偶问题，包括对偶范数，对偶问题和共轭函数等。如果对你有用的话，欢迎点赞！收藏！关注！**（前置知识：凸优化基础理论，线性代数的知识）**
拉格朗日对偶问题与KKT条件
Taylor Wu的专栏
03-01 6238
本篇是写在SVM之前的关于优化问题的一点知识，在SVM中会用到。考虑到SVM之复杂，将其中优化方面基础知识提出，单作此篇。所以，本文也不会涉及优化问题的许多深层问题，只是个人知识范围内所了解的SVM中涉及到的优化问题基础。 一、凸优化问题 在优化问题中，凸优化问题由于具有优良的性质（局部最优解即是全局最优解），受到广泛研究。 对于一个含约束的优化问题： {minxf(x)s.t.x∈C
凸优化中的对偶问题
联邦学习小白
07-01 2590
最近看论文里面有好多凸优化、对偶函数、KKT什么的，太顶了，看不下去，就先补一补这方面的知识。 凸优化其实是一个比较大的问题，看了半天也是一知半解，只能理解大概的原理和意义，这里就先记录一下，后面有更深的理解再补充。 我们知道所谓优化就是要去找全局最优解，凸优化是什么，凸优化中的全局最优解怎么找，我们首先从一般的优化问题开始理解。 优化问题的基本形式 minimize f0f_0f0​(x), x∈RnR^nRn subject to fif_ifi​(x)≤0, i=1,…,m；hjh_jhj​(x)=0
凸优化第四章——对偶问题
qq_53766473的博客
12-25 1297
设函数fRn→RfRn→R，则其共轭函数f∗Rn→Rf∗Rn→R为f∗ysupx∈domfyTx−fxf∗yx∈domfsup​yTx−fx))。yTx−fxy^Tx-f(x)yTx−fx在domfdom\ fdomf有上界的所有y∈Rny\in R^ny∈Rn构成了f∗f^*f∗的定义域。性质1：不论fff。
凸优化——对偶问题解题步骤
Patience
01-04 2124
对偶问题解题步骤 1. 根据原始问题写出拉格朗日函数 构造方式为，将原始问题优化的函数，减去所有比例因子乘以大于等于0的式子，得到原始问题的拉格朗日函数 （减去而不是加上的原因是，对偶问题是不断最大化原始问题的下限，从而逼近原始问题的最小值。当原函数为凸函数时，对偶问题的解通常等于原始问题的解。） 2. 根据原始问题写出K.K.T条件 K.K.T条件有： s.t.中 所有...
凸优化——详解对偶和鞍点
weixin_44382951的博客
07-15 2033
强对偶 原问题的最优解（最小解）p∗p^*p∗一定是大于等于其对偶问题的最优解（最大值）d∗d^*d∗的： p∗>=d∗p^*>=d^*p∗>=d∗ 这是对偶问题最重要的一条性质 弱对偶 满足p∗>=d∗p^*>=d^*p∗>=d∗，这就是弱对偶性，无论原函数是不是凸的，只要有解就一定满足前述不等式，也就是说一定都是弱对偶的。 强对偶 如果一个问题p∗=d∗p^*=d^*p∗=d∗，那原问题和对偶问题就是强对偶的。也就是最优对偶间隙p∗−d∗p^*-d^*p∗−d∗为0
《凸优化》——Stephen Boyd
这本书详细介绍了数学优化、线性规划、非线性优化以及凸优化的核心概念，是理解和应用凸优化问题的重要参考资料。" 在本书中，作者首先通过【描述】引出数学优化的基础，包括最优化问题的定义，以及线性规划和最小...
《凸优化》——Stephen Boyd & Lieven Vandenberghe
通过对偶问题，可以得到原问题的下界，甚至有时可以得到原问题的最优解。对偶理论是凸优化中的核心内容，因为它提供了解决复杂问题的有效途径，如松弛和乘子方法。 5. **其他章节**：除了以上内容，书中可能还包括...
拉格朗日对偶及凸优化
03-26
主要介绍拉格朗日对偶及凸优化，拉格朗日对偶函数。包括拉格朗日对偶问题，强对偶和Slater’s条件，KKT最优化条件，敏感度分析
凸优化学习-（十九）深入分析对偶问题
欢迎你
03-23 916
凸优化学习 学习笔记 一、原问题最优值p∗\text p^*p∗与与对偶问题最优值d∗\text d^*d∗分析 1、背景知识 对于一个普通优化问题： min⁡f0(x)(P)s.t.fi(x)≤0i=1⋯mhi(x)=0i=1⋯p \begin{aligned} \min&& f_0(x)&\\ (\text P)\qquad\text{s.t.}&&...
凸优化基础知识—对偶（Duality）
技术并不是我们的全部
07-06 2832
Directory对偶（Duality）拉格朗日对偶函数（The Lagrange dual function）A. 拉格朗日（Lagrange）B. 朗格朗日对偶函数（The Lagrange dual function）C. 最优值的下界（Lower bounds on optimal value）例子（Examples）线性等式的最小二乘解（Least-squares solution of linear equations）D. The Lagrange dual function and co..
凸优化理论学习五|对偶性
weixin_47748259的博客
05-18 1223
对偶问题（Dual Problem）在优化理论中是与原始问题相关联的一个问题。对偶问题的目标函数和约束条件是通过拉格朗日函数构造的，其形式可能有所不同，具体取决于原始问题的形式。目标函数：最大化gλvgλvλ≥0λ≥0凸性：无论原始问题是否为凸，对偶问题始终为凸优化问题，因此对偶问题比原始问题更容易求解弱对偶性：对于任何原始可行解xxx和任何对偶可行解λvλvfx≤gλvfx≤gλv。
凸优化与对偶(1)
Geek
03-10 320
课程目录 AI问题和程序的类比 优化问题的表示方法 需要做到闭着眼睛也能写XD 预训练（例如ImageNet pretrainning, word2vector等）是为了找到更好的初始化点，因为初始化对local optimal影响很大。 ...
凸优化中的对偶（Duality in General Programs）
zbwgycm的博客
03-09 3790
Intorduction 在上节中，我们讨论了线性规划中的对偶，引入了对偶的基本概念和对偶的两种解释。对偶相当于给当前的优化问题找到了一个下界，通过提升这个下界来找到原问题的最优解。本节将进一步介绍对偶在一般规划问题中的推广。 拉格朗日对偶函数 考虑一般的最小化问题： min⁡xf(x)subject tohi(x)≤0, i=1,...,mli(x)=0, j=1,...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值