2022-ICLR-Geometric and Physical Quantities Improve E(3) Equivariant Message Passing

2022-ICLR-Geometric and Physical Quantities Improve E(3) Equivariant Message Passing

Paper: https://arxiv.org/abs/2110.02905
Code: https://github.com/RobDHess/Steerable-E3-GNN
Blog:https://robdhess.github.io/Steerable-E3-GNN/
Video: https://www.youtube.com/watch?v=jKXMgaC1oHE

几何和物理量改进了 E(3) 等变消息传递

本文是来自于2022 ICLR的论文，其内容主要是：在很多计算物理学和化学任务中考虑协变信息（例如，位置、力、速度和旋转）是非常重要的。作者引入了 Steerable E(3) Equivariant Graph Neural Networks (SEGNNs)，它概括了等变图网络，使得节点和边属性不限于不变标量，而是可以包含协变信息，例如向量或张量。该模型由可操纵的 MLP 组成，能够在消息和更新函数中结合几何和物理信息。通过可控节点属性的定义，MLP 提供了一类新的激活函数，可用于可控特征字段。能够确定 SEGNN 为成功组件:非线性消息聚合改进了经典的线性（可控）点卷积；可控消息改进了最近发表不变消息的等变图网络。并证明了该方法在计算物理和化学的多项任务中的有效性，并提供了广泛的消融研究。

介绍

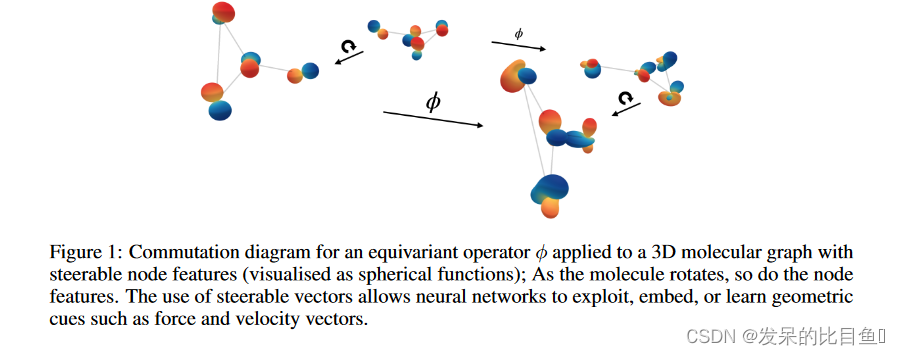
如图1分子图所示，该方法的核心是使用可控向量及其等变变换来表示和处理节点特征。节点和边上的信息现在可以是旋转不变的（标量）或协变的（向量、张量）。在可控消息传递框架中，Clebsch-Gordan (CG) 张量积用于通过相对方向（姿态）等几何信息来控制更新和消息函数。节点属性可以包括节点速度、力或原子自旋等信息。目前，尤其是在分子建模中，大多数数据集仅由原子序数和位置信息组成。在本文中， 作者展示了使用更多几何和物理量来丰富节点属性的潜力。通过在 n-body toy数据集上设置最新技术水平来证明 SEGNN 的有效性，该方法利用了丰富的可用几何和物理量。作者在分子数据集 QM9 和 OC20 上测试该模型。虽然这里只有（相对）位置信息作为几何量可用，但 SEGNN 在 OC20 的 IS2RE 数据集上实现了最先进的技术水平，并且在 QM9 上具有竞争性能。

本文的主要贡献是：

• (i) 等变 GNN 的推广，使得节点和边缘属性不限于标量。
• (ii) 基于可控节点属性和可控多层感知器的引入，用于可控矢量场的一类新的等变激活函数，允许将几何和物理量注入节点更新。
• (iii) 通过非线性卷积的定义对各种等变 GNN 的统一观点。
• (iv) 广泛的实验性消融研究表明可控消息传递优于不可控（不变）消息传递，以及非线性卷积优于线性卷积。

广义 E(3) 等变可控消息传递

Message passing networks. 考虑一个图 $G=(V,E)$，节点 $v_i\in V$ 和边 $e_{ij}\in E$，特征向量 $f_i\in R^{cn}$ 附加到每个节点，边属性 $a_{ij}\in R^{ce}$ 附加到每条边。

其中 $N(i)$ 表示节点 $v_i$ 的邻居集，并且 ${\phi }_m$ 和 ${\phi }_f$ 通常由多层感知器 (MLP) 参数化。

Equivariant message passing networks 构建对旋转、反射、平移和排列具有鲁棒性的图神经网络。这是一个理想的属性，因为一些预测任务（例如分子能量预测）需要 E(3) 不变性，而其他任务（例如力预测）需要等变性。从技术角度来看，函数 $\phi$ 对某些变换的等变性意味着对于任何变换参数 $g$ 和所有输入 $x$，有 $T_g^{\prime }[\phi (x)]=\phi (T_g[x])$ ，其中 $T_g$ 和 $T_g^{\prime }$分别表示 $\phi$ 的输入域和输出域的变换。应用于原子图的等变算子使能够保留系统的几何结构，并通过越来越抽象的方向信息来丰富它。将等式 (1-2) 的函数 ${\phi }_m$ 和 ${\phi }_f$ 约束为等变来构建 E(3) 等变 GNN，这反过来保证了整个网络的等变性。

可操纵 MLP 的数学背景

---

可操纵 MLP 的数学背景。

1. 群定义和群示例。整个框架建立在组论的概念之上，因此正式定义是有序的。在本文中，将平移、旋转和反射等转换建模为群。

2. 不变性、等变性和表示。如果一个函数的输出不受输入变换的影响，则称该函数对变换具有不变性。如果函数的输出在输入变换下可预测地变换，则称该函数是等变的。为了使定义精确，需要表示的定义；表示形式化了在组论背景下应用于向量的变换的概念。

3. 可控向量、Wigner-D 矩阵和不可约表示。常规 MLP 使用元素为标量的特征向量，而可控 MLP 使用由可控特征向量组成的特征向量。可控特征向量是通过所谓的 Wigner-D 矩阵变换的向量，它是正交组 O(3) 的表示。Wigner-D 矩阵是最小可能的组表示，可用于定义任何表示（或者相反，任何表示都可以通过基的变化简化为 Wigner-D 矩阵的张量积）。因此，Wigner-D 矩阵是不可约表示。

4. 球面谐波。球谐函数是球体 $S^2$ 上的一类函数，可以被认为是球体上的傅里叶基。表明球谐函数由 Wigner-D 矩阵控制，并将可控制向量解释为 S2 上的函数，这证明了本文中使用的字形可视化。

5. Clebsch-Gordan 张量积和可控 MLP。在常规 MLP 中，通过矩阵向量乘法在输入和输出向量空间之间线性映射，然后应用非线性。在可控 MLP 中，通过 Clebsch-Gordan 张量积在可控输入和可控输出向量空间之间映射。类似于常规 MLP 中的可学习权重矩阵，可学习的 Glebsch-Gordan 张量积是可操纵 MLP 的主力。

---

Steerable features 通过使用可操纵的特征向量来实现等变图神经网络，用波浪号表示，例如矢量$\tilde{h}$是可控的。向量的可导性是指对于某个变换参数为$g$ 的变换群，向量通过矩阵-向量乘法$D(g)\tilde{h}$进行变换。例如，$R^3$ 中的欧几里德向量可通过将向量与旋转矩阵相乘来控制旋转 $g=R\in SO(3)$，因此 $D(g)=R$。然而，并不仅限于使用 3D 矢量；通过构建可控向量空间，将 3D 旋转的概念推广到任意大的向量。核心是使用 Wigner-D 矩阵 $D^{(l)}(g)$。这些是作用于 $(2l+1)$维向量空间的 $(2l+1\times 2l+1)$ 维矩阵表示。这些由l次Wigner-D矩阵变换的向量空间称为l型可导向量空间，记为$V_l$。通过直和组合两个独立的 $l_1$ 和 $l_2$ 类型的可导向量空间 $V_{l_1}$ 和 $V_{l_2}$，记为 $V=V_{l_1}\oplus V_{l_2}$ 。这样的组合向量空间然后通过Wigner-D矩阵的直接和进行变换，即通过 $D(g)=D^{(l_1)}(g)\oplus D^{(l_2)}(g)$，这是一个块对角矩阵，其中沿对角线的 Wigner-D 矩阵。将 l 型向量空间的直和表示为$l=L$ 以$V_L:=V_0\oplus V_1\oplus \cdot \cdot \cdot \oplus V_L$和 $n$ 个具有 $nV:=\underset{n-times}{\underbrace{V\oplus V\oplus ...V}}$ 的相同向量空间的副本。常规 MLP 基于 $d$ 维类型 0 向量空间之间的转换即，$R^d=d{V}_0$，并且是可操纵 MLP 的一个特例，它作用于任意类型的可操纵向量空间。

Steerable MLPs. 与常规 MLP 一样，可控 MLP 是通过交织线性映射（矩阵向量乘法）和非线性来构建的。然而现在，线性映射通过$\widetilde{h^i}=W_{\tilde{a}}^i{\tilde{h}}^{i-1}$ 在第 $i-1$ 层的可操纵向量空间到第 $i$ 层之间变换。因此，可控 MLP 具有与常规 MLP 相同的函数形式。然而，在这项工作中，作者将使用向量$\tilde{a}$ 对几何和结构信息进行编码，并引导 $\tilde{h}$ 的信息流通过网络。为了保证 $W_{\tilde{a}}^i$在可操纵向量空间之间映射，矩阵通过 Clebsch-Gordan 张量积定义。通过构造，生成的 MLP 对于每个变换参数 $g$ 都是等变的

前提是调节 MLP 的可操纵向量 $\tilde{a}$ 也是等变地获得的。

Spherical harmonic embedding of vectors. 通过球谐函数的计算将任意向量 $x\in R^3$ 转换为 $l$ 型向量$Y_m^{(l)}:S^2\to R$, 在$\frac{x}{||x||}$.对于任何$x\in R^3$是 l 型可控向量。

球谐函数 $Y_m^{(l)}$ 是球体 $S^2$ 上的函数，在图 2 中将它们可视化。并将使用球谐函数嵌入将几何和物理信息包含到可操纵的 MLP 中。

Mapping between steerable vector spaces.

Clebsch-Gordan (CG) 张量积 ${\otimes }_{cg}:V_{l_1}\times V_{l_2}\to V_l$ 是一个双线性算子，它结合了两个 O(3) 类型 $l_1$ 和 $l_2$ 的可控输入向量，并返回另一个 $l$ 类型的可控向量。设 ${\tilde{h}}^{(l)}\in V_l=R^{2l+1}$ 表示 l 类型的可操纵向量，$h_m^{(l)}$ 表示其分量，其中 $m=-l,-l+1,...l.$CG 张量积由下式给出

其中 $w$ 是缩放乘积的可学习参数，$C_{(l_1,m_1)(l_2,m_2)}^{(l,m)}$ 是 ClebschGordan 系数，可确保生成的向量是类型 $l$ 可控的。CG 张量积是一种稀疏张量积，因为通常许多系数为零。最值得注意的是，只要 $l<|l_1-l_2|，C_{(l_1,m_1)(l_2,m_2)}^{(l,m)}=0$或 $l>l_1+l_2$。而方程式 (5) 只描述单一类型的可操纵向量之间的乘积, 例如$h^{(l_1)}\in V_{l_1}$ 和 ${\tilde{h}}^{(l_2)}\in V^{l_2}$ ，它可以直接扩展到混合类型的可操纵向量，该向量可能在一个类型中具有多个通道/多重性。在这种情况下，输出子向量对的每个输入都以类似于标准线性层中的权重使用输入输出索引进行索引的方式获得自己的索引。然后，用带有粗体 $W$ 的 ${\otimes }_{cg}^W$ 表示 CG积，以表明它是由一组权重参数化的。为了接近 MLP 使用的标准，将在其输入之一中具有固定向量$\tilde{a}$ 的 CG积视为以$\tilde{a}$为条件的可控线性层，

其中后者表示 CG 权重取决于某个数量 d，例如相对距离。

Steerable activation functions. 深度神经网络的常用方法是将线性层与逐元素非线性激活函数交替使用。在可控设置中，需要仔细考虑以确保激活函数是等变的；目前可用的激活类别包括基于傅里叶的、规范改变（Thomas 等人，2018 年）或门控非线性。在所有架构中使用门控非线性，并在第 2 节中简要讨论它们的工作原理在附录C中。由此产生的可控 MLP 本身又提供了一类新的可控激活函数，这是同类中第一个直接利用局部几何线索的函数。即，通过可控节点属性$\tilde{a}$，从物理设置（力、速度）或预测（类似于门控）。MLP 可以按节点应用，并且通常作为非线性激活用于可操纵的特征场。

可控 E(3) 等变图神经网络

扩展消息传递方程 (1)-(2) 并定义一个消息传递层，通过以下步骤更新节点 $v_i$ 处的可控节点特征 ${\tilde{f}}_i\in V_L$：

这里，$\Vert xj-xi{\Vert }^2$ 是两个节点 $v_i$ 和 $v_j$ 之间的平方相对距离，${\phi }_m$ 和 ${\phi }_f$ 是 O(3) 可控 MLP，$\widetilde{a_{ij}}\in V_L$ 和 $\widetilde{a_i}\in V_L$ 是可控边和节点属性。如果存在其他属性，例如成对距离$\Vert x_j-x_i\Vert$，则可以将它们连接到调节可操纵 MLP 的属性，或者像更常见的做法一样，将它们添加为 ${\phi }_m$ 和 ${\phi }_f$ 的输入。作者使用了后者，并将所有输入堆叠到一个单一的可控向量，通过该向量给出可控 MLP 层：${\tilde{h}}^1=\sigma (W{\tilde{a}}_{ij}{\tilde{h}}_i^0)$ , 其中 ${\tilde{h}}_i^0=({\tilde{f}}_i,{\tilde{f}}_j,\Vert x_j-x_i{\Vert }^2)\in V_f\oplus V_f\oplus V_0$,其中 $V_f$ 是用户指定的节点表示的可操纵向量空间。消息网络 ${\phi }_m$ 通过边属性${\tilde{a}}_{ij}$ 进行控制，节点更新网络 ${\phi }_f$ 类似地通过节点属性 ${\tilde{a}}_i$ 进行控制。

Injecting geometric and physical quantities. 为了使 SEGNN 更具表现力，在边和节点更新中包含几何和物理信息。为此，边缘属性是通过相对位置的球谐函数嵌入(等式(4))获得的，在大多数情况下，但也可能是相对力或相对动量。节点属性可以例如是节点邻居上相对位置的平均边缘嵌入， 即 ${\tilde{a}}_i=\frac{1}{|N(i)|}{\sum }_{j\in N(i)}{\tilde{a}}_{ij}$,并且还可以包括节点力、自旋或速度，在 $N-body$实验中所做的那样。在定义 ${\phi }_f$ 的可操纵 MLP 中使用可操纵节点属性使不仅可以将几何线索集成到消息函数中，还可以在节点更新中利用它。

消息传递作为卷积

作者将任何等变的非线性运算符称为非线性卷积，它可以用简单的消息传递形式编写。该架构的两个重要方面：、

• (i) 等变层改进不变层，
• (ii) 非线性层改进线性层。
  两者通过可控非线性卷积在 SEGNN 中结合在一起。

Point convolutions as equivariant linear message passing.

考虑一个特征映射 $f:R^d\to R^{cl}$ 。具有逐点非线性 σ 的卷积层（通过互相关定义）由下式给出

其中 $W:R^d\to R^{c_{l+1}\times c_l}$ 是一个卷积核，它为每个相对位置提供一个矩阵，该矩阵将特征从 $R^{cl}$ 线性变换到 $R^{c_{l+1}}$ 。对于由局部特征对$(x_i,f_i)$ 组成的稀疏输入特征图，点卷积由 $f_i^{\prime }={\sum }_{j\in N(i)}W(x_j-x_i)f_i$ 给出，它描述了一个线性消息传递层方程式(1)-(2) 其中消息为 $m_{ij}=W(x_j-x_i)f_j$ 并且消息更新 $f_i^{\prime }={\sum }_j{m}_{ij}$。在上述卷积中，变换矩阵 $W$ 以相对位置 $x_j-x_i$ 为条件，这通常通过以下三种方法之一完成:

• (i) 特征图是在具有共享邻域的密集规则网格上处理的，因此变换 $W_{ij}$ 可以存储在单个张量中的一组有限的相对位置 $x_j-x_i$ 中。然而，这种方法不能推广到不均匀的网格，例如点云。连续核方法通过以下方式对转换进行参数化。
• (ii) 将 $W$ 扩展为连续基
• (iii) 通过 $W(x_j-x_i)=MLP(x_j-x_i)$ 用 MLP 直接对它们进行参数化。可控核方法属于 (ii) 类型并依赖于可控基，例如 3D 球谐函数 $Y_m^{(l)}$

通过

基系数 $W_m^{(l)}$ 通常取决于成对距离。

Steerable (group) convolutions. 线性特征变换$W$等价于以标量“1”为条件的可控线性变换（等式(6))。即，在通常的 $h_i\in R^d$ 和 $\tilde{h}\in d{V}_0$ 的可控设置中，消息通过以下方式获得

当在可控基础 (10) 中对变换进行参数化,

其中 ${\tilde{a}}_{ij}=Y_m^{(l)}(x_j-x_i)$ 是 $x_j-x_i$ 的球谐嵌入(等式(4))，参数化 CG 张量积的权重取决于成对距离。

卷积结果:

通过与可控内核的卷积获得的可控矢量，通过 Wigner-D 矩阵在 O(3) 上生成信号。这种关系实际上是由 O(3) 上的傅里叶逆变换建立的，通过它可以将每个位置 $x_i$ 处的可操纵特征向量 ${\tilde{f}}_i$ 视为群 $O(3)$ 上的函数。正是这种通过群作用（通过 $W(g^{-1}\cdot x_j)=W(R^{-1}(x_j-x))$变换卷积核的机制构成了群卷积的基础。在实验中比较的等变可控方法都可以写成卷积形式

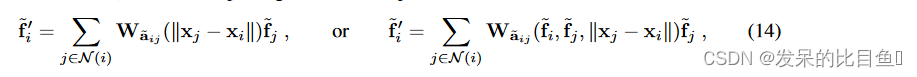
其中，在后一种情况下，线性变换还依赖于依赖于输入的注意力机制，并且可以看作是注意力组卷积的可控 PointConv 版本。在这些基于注意力的情况下，通过$W_{{\tilde{a}}_{ij}}({\tilde{f}}_i,{\tilde{f}}_j,\Vert x_j-x_i\Vert )=\alpha ({\tilde{f}}_i,{\tilde{f}}_j)W_{{\tilde{a}}_{ij}}(\Vert x_j-x_i\Vert )$ 增加了与输入相关的权重$\alpha$).

Equivariant message passing as non-linear convolution.

这有点令人惊讶，因为它发送不变的消息，这些消息是通过 $h_i=(f_i,f_j,\Vert x_j-x_i{\Vert }^2)$ 形式的 MLP 获得的。由于它们依赖于相对位置，这些消息类似于点卷积的卷积消息。但是，有两个重要的区别：

• (i) 消息是通过 MLP 对相邻特征值 $f_j$ 的非线性变换，
• (ii) 消息仅以点对之间的距离为条件，因此是 E(n) 不变的。因此，将 EGNN 层视为具有各向同性消息函数的非线性卷积（旋转不变内核的非线性对应物）。

各向同性约束并通过以下形式的消息推广到非线性可控卷积

其中${\tilde{h}}_i=({\tilde{f}}_i,{\tilde{f}}_j,\Vert x_j-x_i{\Vert }^2)\in V_f\oplus V_f\oplus V_0$。然后 MLP 以属性 ${\tilde{a}}_{ij}$ 为条件，例如是 $x_j-x_i$ 的球谐嵌入。这允许创建比在卷积中发现的消息更通用的消息，同时携带协变几何信息。

Related equivariant message passing methods. 与将等变信息视为完全可控特征的 SEGNN 相比，这些架构使用向量值属性的范数更新标量值属性，因此具有 O(3) 不变信息。这些方法限制了不同类型属性之间的信息流，而 SEGNN 中的 ClebschGordan 张量积允许整个网络中所有阶次的球谐函数之间的相互作用。

实验

实施细节

SEGNN 的 O(3) 可控 MLP 的实现基于 e3nn 库。要么将可操纵向量空间定义为 $V=n{V}_L=l_{max}$（N 体，QM9 实验），即 $n$ 个可操纵向量空间的副本，最高为 lmax 阶，或者通过将 n 维向量空间 V 划分为大致相等大的 L l 型子向量空间（OC20 实验），如 Finzi 等人所做的那样。

SEGNN 架构和消融

在所有的任务中，作者都至少设置了一个完全可控的SEGNN。作者进行了消融实验来研究使SEGNN和文献不同的两个主要原则。A1非可控vs可控的情形通过在lf、la中设置不同的最大球谐阶所得到。那么EGNN可以当成lf=0,la=0的特殊情形。这些模型用SEGNN标记。A2使用可控等变点卷积方式（Thomas等人在2018年的工作），将其和通过两层可控MLPs非线性方式实现的网络进行对比。

N-body system

带电N-body系统实验包含五种带正电荷或者负电荷的例子，并给定它们的初始三维位置和速度。任务是估计在1000个时间步后粒子的位置。

结果和消融研究如表1所示。当lf=1,la=1可控架构取得最佳效果，增加阶数并不会提高性能。SEGNN(G)模型只利用了几何信息，具体是将边的属性（如相对取向）进行平均作为节点属性。而SEGNN(G+P)在前者的基础上，将速度的球谐编码加入到节点属性中。从表1中可以看出，SEGNN(G+P)性能相对于SEGNN(G)又有所提升。

QM9

QM9数据集包含拥有29种原子的小分子，并使用三维位置坐标和表示原子类型的独热编码来描述每一个原子。任务是通过优化预测和基本事实之间的平均绝对误差来回归出各种分子的化学性质。

如表3所示，随着可控特征向量阶数提高，性能也随之提高，对于小的cutoff radius尤其明显。表2和表3共同表明SEGNNs表现优于架构可比的EGNN模型，同时从中剥离出注意力模块并且将图的连接性进行缩减。

OC20

Open Catalyst Project OC20数据集由表面上的molecular adsorptions组成。作者关注的是Initial Structure to Relaxed Energy（IS2RE）任务，该任务将输入作为初始结构并预测最终的能量。最终的测试集分为四类，in-distribution（ID）催化剂和吸附物、out-of-domain吸附物（OOD Ads）、out-of-distribution催化剂(OOD Cat)、out-of-distribution（OOD Both）吸附物和催化剂。

表4展示了在OC20数据集上SEGNN模型和其它模型的对比。通过消融研究得到了最好的SEGNN模型，该模型基本在所有指标上都取得最先进的结果。

结论

引入了 SEGNN，它概括了等变图网络，这样节点和边缘信息不限于不变（标量），也可以是向量值或张量值。SEGNN 是第一个允许通过利用几何和物理线索来引导节点更新的网络，引入了一类新的等变激活函数。通过将 SEGNN 应用于各种不同的任务来展示它的潜力。广泛的消融研究进一步显示了可控消息传递优于不可控（不变）消息传递，以及非线性卷积优于线性卷积的优势。在 OC20 ISRE 任务中，SEGNN 的表现优于所有竞争对手。