《计算机控制理论与应用》MATLAB示例

最新推荐文章于 2023-06-15 00:41:51 发布

Olefine1999

最新推荐文章于 2023-06-15 00:41:51 发布

阅读量3.4k

点赞数 4

本文链接：https://blog.csdn.net/weixin_42657460/article/details/106384556

版权

MATLAB Mobile的安装与使用

在这里插入图片描述

安装与使用：
App Store - MATLAB Mobile - 安装
文件 - 新建脚本 - m文件；命令 - 命令行
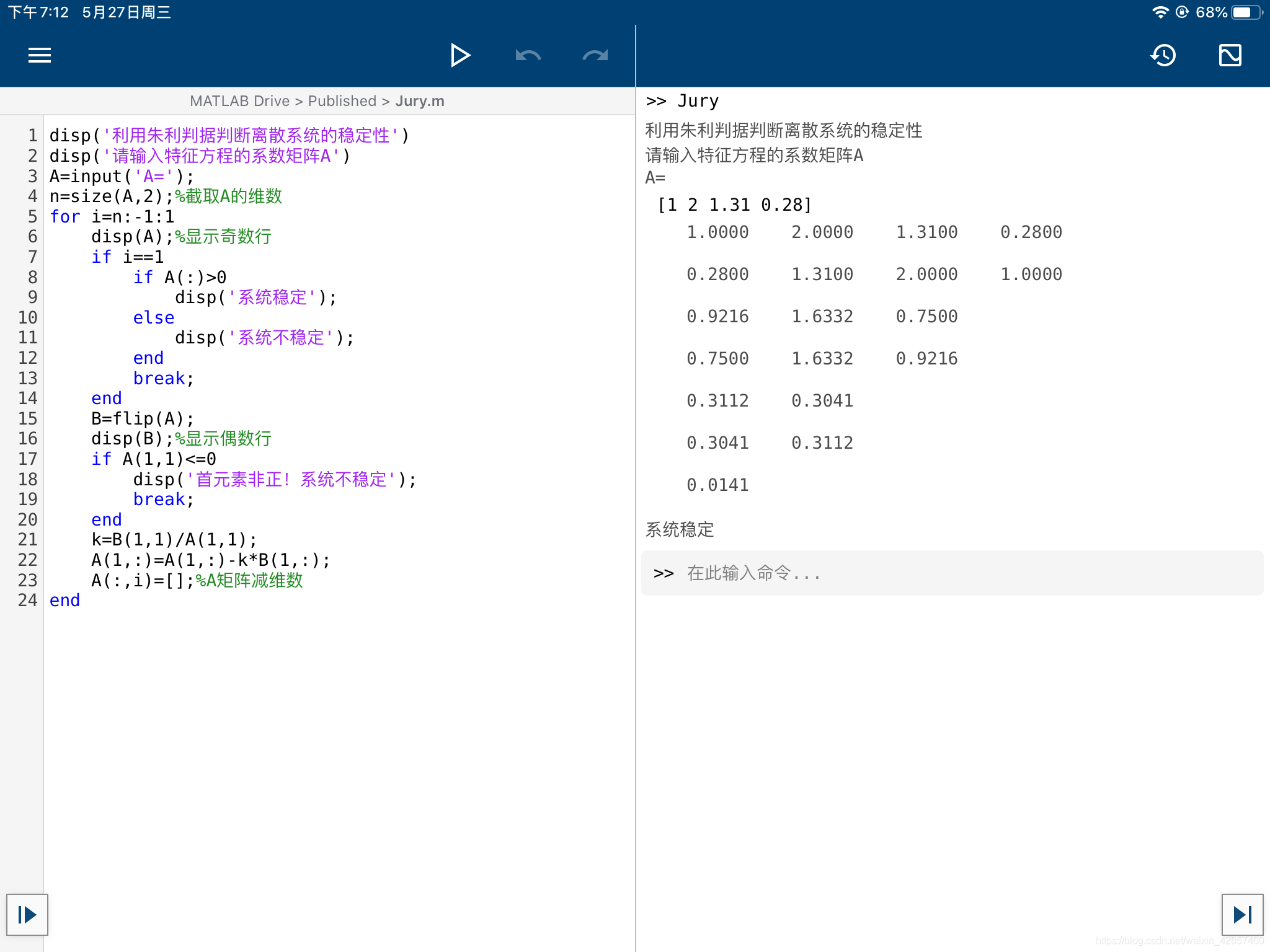
在这里插入图片描述
（脚本示例如上图）

（命令行示例如上图）

创建Mathworks账户
最好用电脑创建账户，直接浏览器搜索Mathworks进入官网创建即可。
安装Control System Toolbox
Control System Toolbox的功能很强大，为系统化地分析、设计和调节线性控制系统提供算法和应用程序。
由于我们在电脑上基本安装的都是破解版的MATLAB，所以我们自己创建的Mathworks账户都是没有关联许可证的，也就无法安装toolbox。有一个解决方法是，直接浏览器搜索 Control System Toolbox，进入官网点击“试用软件”，安装后可免费使用30天。这样，就能在手机上使用tf、c2d等函数了。

Chapter 2

基本函数

在MATLAB中表示Z传递函数

% 返回脉冲传递函数，Hd = tf(num,den,Ts),Ts = -1时，表示采样周期未定义
Hd = tf([0.01 0.03 -0.07], [1 -2.7 2.42 -0.72],-1);

在这里插入图片描述

离散zero/pole/gain模型与Z传递函数的形式转换

% z传递函数的形式转换，多项式形式转换为零极点形式
Hd = tf(10,[1 1 0],-1);
Hd = zpk(Hd);

在这里插入图片描述

% z传递函数的形式转换，零极点形式转换为多项式形式
Hd = tf(Hd);

在这里插入图片描述

常用变换对
首先，需要安装Symbolic Math Toolbox工具箱，方法同Control System Toolbox。

% 1.傅里叶变换
syms x; % 定义符号变量x
fourier(x); % 对x求傅里叶变换，变换后的变量默认为w
% 2.傅里叶反变换
syms w;
ifourier(w^2); % 对w^2求傅里叶反变换，变换后的变量默认为x
% 3.拉普拉斯变换
syms t;
laplace(t+1); % 对t+1求拉普拉斯变换，变换后的变量默认为s
% 4.拉普拉斯反变换
syms s;
ilaplace(1/s); % 对1/s求拉普拉斯反变换，变换后的变量默认为t
% 5.Z变换
syms n T;
ztrans(n*T); % 对n*T求Z变换，自变量默认为n，变换后的变量默认为z
% 6.Z反变换
syms z;
iztrans(z/(z-1)); % 对z/(z-1)求Z反变换，变换后的变量默认为n

结果5如下图：
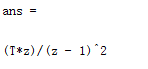
在这里插入图片描述

S变换与Z变换

已知采样周期Ts：

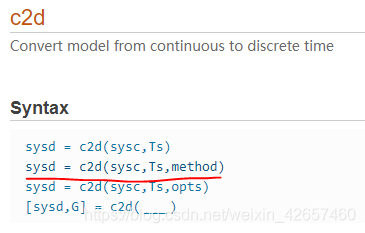
在这里插入图片描述

例1：求 $\frac{1}{s(s+1)}$ 的Z变换

hc = tf(1,[1,1,0]);
hd = c2d(hc,1,'imp');  % Ts = 1,'imp'表示脉冲响应不变法，即直接z变换

结果如图：
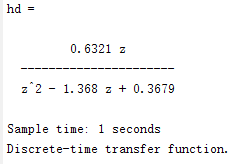
在这里插入图片描述
例2：含零阶保持器

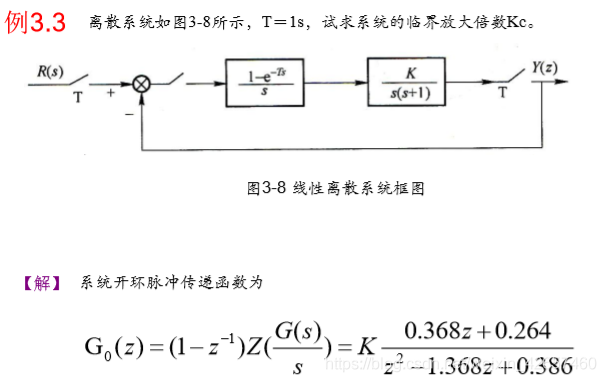
MATLAB程序中令K = 1：

hc = tf(1,[1,1,0]);
hd = c2d(hc,1); % Ts = 1, method 默认为‘zoh’

结果如图：
在这里插入图片描述

未知采样周期Ts：
（1）Z变换

syms z s T;
F = input('F(s)=');                %z域象函数
[n1,m] = numden(F);
root = solve(m==0,s)';             %符号型
root1 = double(root);               %浮点型
G = simplify(F*z/(z-exp(s*T)));          %这个simplify合并
Results = 0;
tabu = [];                        %计算过的极点就加入这个数组
for i = 1:length(root)
    R = root1(i);
    if(sum(tabu==R)>0)
        continue
    end
    n = sum(root1==R);             %计算极点的重数
    if n==1
        H = G*(s-root(i));
        H = subs(H,s,root(i));
    end
    if n>=2
        H = G*(s-R)^n;
        for j = 1:n-1
            H = diff(H,s);
        end
        H = sym(1/(factorial(n-1)))*H;
        H = subs(H,s,R);
    end
    Results = Results + H;
    tabu = [tabu,R];
end
    if n>=2
        H = G*(s-R)^n;
        for j = 1:n-1
            H = diff(H,s);
        end
        H = sym(1/(factorial(n-1)))*H;
        H = subs(H,s,R);
    end
        if n==1
        H = G*(s-root(i));
        H = subs(H,s,root(i));
        end
disp('z变换结果：')
Fz = simplify(Results)

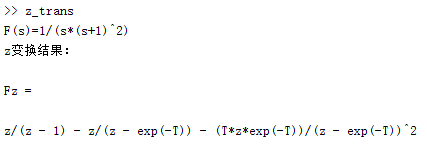
在这里插入图片描述
（2）Z反变换：

syms z k;
F = input('F(z)=');                %z域象函数
[n1,m] = numden(F);
coff = sym2poly(n1);                %多项式系数提取
if(coff(1,end)==0)                  %判断是否需要单独计算0处
    key = 1;
else 
    key=0;
    F0 = limit(F,z,inf);
end
root = solve(m==0,z)';             %符号型
root1 = double(root);               %浮点型
G = simplify(F*z^(k-1));          %这个simplify把k-1项合进F而不是单纯显示乘法，不这样后面可能报错
Results = 0;
tabu = [];                        %计算过的极点就加入这个数组
for i = 1:length(root)
    R = root1(i);
    if(sum(tabu==R)>0)
        continue
    end
    n = sum(root1==R);             %计算极点的重数
    if n==1
        H = G*(z-root(i));
        H = subs(H,z,root(i));
    end
    if n>=2
        H = G*(z-R)^n;
        for j = 1:n-1
            H = diff(H,z);
        end
        H = sym(1/(factorial(n-1)))*H;
        H = subs(H,z,R);
    end
    Results = Results + H;
    tabu = [tabu,R];
end
if(key == 1)
    Ft = simplify(Results)
else 
    disp('t=0T时：');
    F0
    disp('t>0T时');
    Ft = simplify(Results)
end

差分方程求解（WolframAlpha）

在这里插入图片描述
推荐使用：
WolframAlpha 手机App（付费） / 网页版（免费）

WolframAlpha还可计算Fourier，Laplace，Z变换等

由Z传递函数求离散状态方程

Z传递函数求离散状态方程包括：并行程序法、串行程序法、直接程序法、嵌套程序法，如果想要通过 MATLAB 中自带的函数进行求解，得到的离散状态方程是直接程序法的结果（但状态变量的顺序和习惯有所不同）。
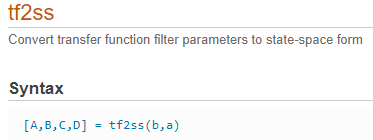
在这里插入图片描述

[A B C D] = tf2ss([2 3 0.2],[1 -1.96 0.8]);

a为直接程序法，b为 MATLAB 中 tf2ss 函数结果：
在这里插入图片描述

连续状态方程的离散化

在这里插入图片描述

% [Ad,Bd,Cd,Dd] = c2dm(A,B,C,D,Ts,'method'), method 缺省为 zoh
A = [-3 1;-2 0];
B = [0;1];
C = [1 0];
D = 0;
[A B C D] = c2dm(A,B,C,D,1)

结果如图（C和D不变）：
在这里插入图片描述

由离散系统状态空间方程求Z传递函数

在这里插入图片描述

syms z
A = input('A=');
B = input('B=');
C = input('C=');
D = input('D=');
x = size(A);
m = x(1);
n = x(2);
A1 = (eye(m,n)*z-A)^(-1);
G = C*A1*B

离散系统状态方程求解 - Z变换法

% 离散状态空间方程的解析解
syms z k
A = input('A=');
B = input('B=');
x0 = input('x0=');
Uz = input('Uz=');
s = size(A);
Ak = iztrans((z*eye(s(1),s(2))-A)^(-1)*z);
Bk = iztrans((z*eye(s(1),s(2))-A)^(-1)*B*Uz,k);
Xk = Ak*x0 + Bk;

在这里插入图片描述

Chapter 3

Jury判据

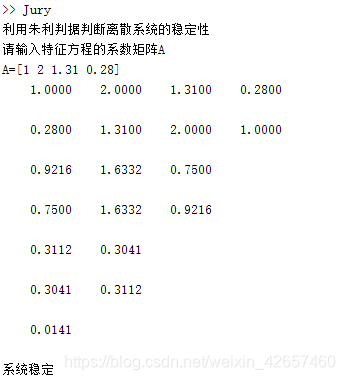
disp('利用朱利判据判断离散系统的稳定性')
disp('请输入特征方程的系数矩阵A')
A=input('A=');
n=size(A,2);%截取A的维数
for i=n:-1:1
    disp(A);%显示奇数行
    if i==1 
        if A(:)>0
            disp('系统稳定');
        else
            disp('系统不稳定');
        end
        break;
    end
    B=flip(A);
    disp(B);%显示偶数行
    if A(1,1)<=0
        disp('首元素非正！系统不稳定');
        break;
    end
    k=B(1,1)/A(1,1);
    A(1,:)=A(1,:)-k*B(1,:);
    A(:,i)=[];%A矩阵减维数
end

例1：已知离散系统的闭环特征方程，试判别该系统的稳定性。

结果如图：

Routh判据

clear;
syms k z q                             %定义变量k z q
p=input('请输入特征多项式的参数 =');   %提示输入参数
n=length(p);                           %得到p的长度
for i=0:ceil(n/2)-1                    %将多项式进行劳斯矩阵排序
    a(1,i+1)=p(2*i+1);
    if 2*(i+1)>n
        a(2,i+1)=0;
        break
    end
    a(2,i+1)=p(2*(i+1));
end
for k=3:n                         %计算从第三行开始劳斯矩阵内容
    for j=1:ceil((n-k+1)/2)
        if a(k-1,1)==0            %判断是否有共轭虚根
            disp('系统有共轭虚根')
            breaksign=1;
            break
        end
        a(k,j)=(a(k-1,1)*a(k-2,j+1)-a(k-1,j+1)*a(k-2,1))/a(k-1,1);
    end
end
disp('劳斯矩阵')                  %输出对应的劳斯矩阵
disp(double(a))
for i=3:k                         %用劳斯判据判断系统的稳定性
    if a(i-1,1)<=0                %判断第一列元素是否不大于0
        q=1; 
        break
    end
end
if q==1
    disp('系统不稳定')
else
    disp('系统稳定')              %输出系统稳定性判定结果
end

例1：带入双线性变换 $\frac{w+1}{w-1}$ 后，使用劳斯判据

结果如图：

离散系统的动态性能分析

例1：分析离散系统的动态性能

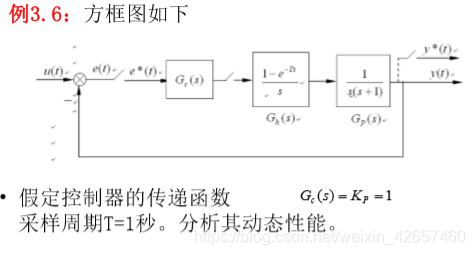
求闭环传递函数Gz：

Gp = tf(1,[1 1 0]);  % Gp(s)
Gpz = c2d(Gp,1);  % 有零阶保持器
Gz = feedback(Gpz,1);  % 闭环传递函数，feedback(a,b)中b为反馈部分

在这里插入图片描述
求阶跃响应曲线：

[num,den]=tfdata(Gz);  % 令num = Gz的分子，令den = Gz的分母
dstep(num,den,20);  % dstep函数用来绘制离散系统的单位阶跃响应，n = 20为指定的输出点个数

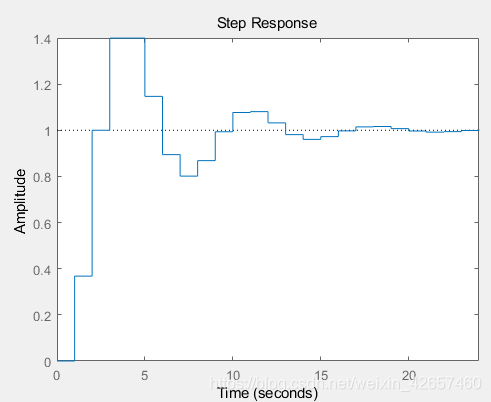
在这里插入图片描述
由图可知：系统的单位阶跃响应序列值、最大超调量、稳态值

根轨迹分析

例1：根轨迹分析离散系统

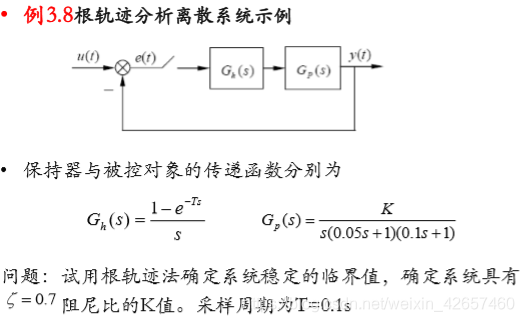
Hc = tf(1,conv([1 0],conv([0.05 1],[0.1 1])));  % Hc = Gp(s)
Hd = c2d(Hc,0.1);  % 有零阶保持器的传递函数离散化，Ts = 0.1
rlocus(Hd);  % 绘制根轨迹

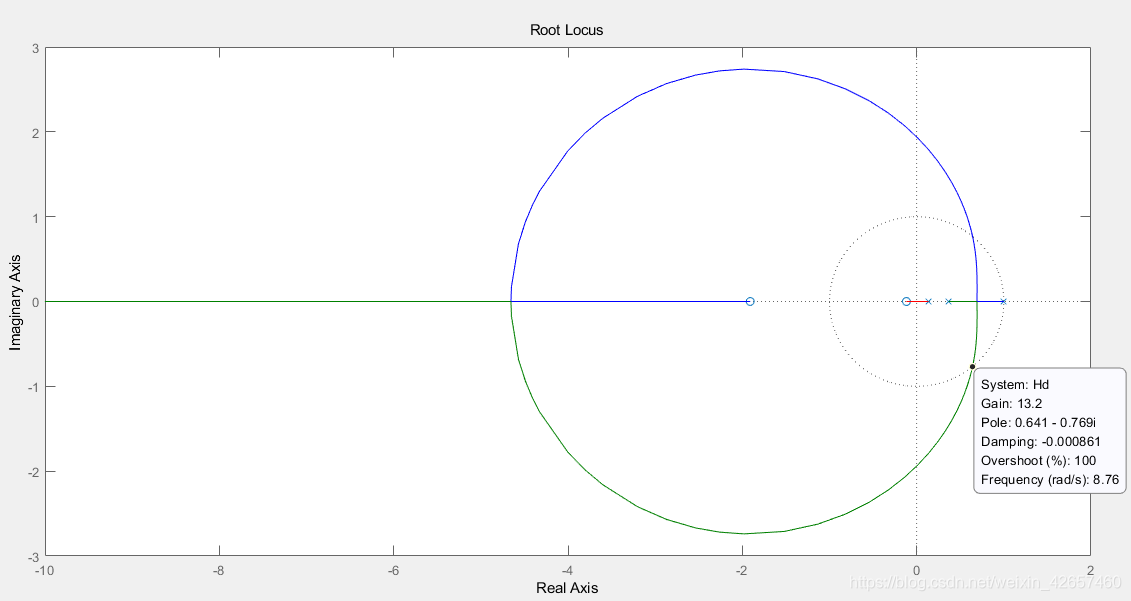
在这里插入图片描述
求零极点：zpk(Hd) 即可
求系统稳定的临界值K：根轨迹与图中虚线部分的交点的Gain值
求阻尼比 = 0.7时的K值：沿着根轨迹移动，当Damping = 0.7时的Gain值

频率特性的分析方法

离散系统极坐标分析法（Nyquist）

% dnyquist: Nyquist frequency response for discrete-time linear systems
num = [1 1]; % 分子部分：z+1
den = conv([1 -1],[1 -0.242]); % 分母部分：(z-1)(z-0.242)
dnyquist(num,den,0.1); % 绘制线性离散系统的Nyquist频率响应曲线，Ts = 0.1

k = 1时，开环幅相特性曲线包围了(-1, j0)，闭环系统不稳定：
在这里插入图片描述
k = 0.5时，开环幅相特性曲线没有包围(-1, j0)，闭环系统稳定：

离散系统对数坐标分析法（Bode）

% dbode: Bode frequency response for discrete-time linear systems
Hc = tf(1,[1 1 0]);
Hd = c2d(Hc,1); % Hd为开环脉冲传递函数
[num den] = tfdata(Hd); % num为Hd的分子系数，den为Hd的分母系数
dbode(num,den,1); % 绘制线性离散系统的Bode图，Ts = 1

在这里插入图片描述

Chapter 4

PID控制器参数对控制系统性能的定量影响

在这里插入图片描述

PID作用定量分析 - 比例

% MATLAB PROGRAM for Proportional Control

G1=tf(1,[0.017 1]); % 电机电枢传递函数
G2=tf(1,[0.075 0]); % 传动装置
G12=feedback(G1*G2,1); % 信号综合点2处的闭环传递函数
G3=tf(44,[0.00167 1]); % 可控硅整流器传递函数
G4=tf(1,0.1925); % 电势系数
G=G12*G3*G4; % 被控对象传递函数G

kp=[1:1:5]; % kp取值从1开始，间距为1，到5结束，即kp为1~5
for i=1:length(kp) 
  Gc=feedback(kp(i)*G,0.01178); % kp取不同值时的系统闭环传递函数
  step(Gc),hold on % 画出阶跃响应
end 
axis([0,0.4,0,130]); 
gtext(['1 Kp=1']); 
gtext(['2 Kp=2']); 
gtext(['3 Kp=3']); 
gtext(['4 Kp=4']); 
gtext(['5 Kp=5']);

在这里插入图片描述

PID作用定量分析 - 积分

%MATLAB PROGRAM for PI Control 

G1=tf(1,[0.017 1]); 
G2=tf(1,[0.075 0]); 
G12=feedback(G1*G2,1); 
G3=tf(44,[0.00167 1]); 
G4=tf(1,0.1925); 
G=G12*G3*G4; 

Kp=1; % 比例系数为1
Ti=[0.03:0.01:0.07]; % Ti取值从0.03开始，间距为0.01，到0.07结束
for i=1:length(Ti) 
  Gc=tf(Kp*[Ti(i) 1], [Ti(i) 0]); % PI环节：Gc = Kp*(Ti*s+1)/Ti*s
  Gcc=feedback(G*Gc,0.01178); 
  step(Gcc),hold on 
end 
axis([0,0.6,0,140]); 
gtext(['1 Ti=0.03']); 
gtext(['2 Ti=0.04']); 
gtext(['3 Ti=0.05']); 
gtext(['4 Ti=0.06']); 
gtext(['5 Ti=0.07']);

在这里插入图片描述

PID作用定量分析 - 微分

% MATLAB PROGRAM for PID Control 
G1=tf(1,[0.017 1]); 
G2=tf(1,[0.075 0]); 
G12=feedback(G1*G2,1); 
G3=tf(44,[0.00167 1]); 
G4=tf(1,0.1925); 
G=G12*G3*G4; 

Kp=0.01; % 比例系数 = 0.01
Ti=0.01; % 积分时间系数 = 0.01
Td=[12:36:84]; % Td取值从12开始，间距为36，到84结束，即取值为12,48,84
for i=1:length(Td) 
  Gc=tf(Kp*[Ti*Td(i) Ti 1], [Ti 0]); % PID环节：Gc = Kp*(Ti*Td*s^2+Ti*s+1)/Ti*s
  Gcc=feedback(G*Gc,0.01178); 
  step(Gcc),hold on 
end 
gtext(['1 Td=12']); 
gtext(['2 Td=48']); 
gtext(['3 Td=84']);

在这里插入图片描述

模拟控制器的离散化方法

以 $\frac{1}{s(s+1)}$ ，Ts = 1 为例：

脉冲响应不变法（Z变换法）

ds = tf(1,[1 1 0]);
y = c2d(ds,1,'imp');

阶跃响应不变法（加零阶保持器的Z变换法）

ds = tf(1,[1 1 0]);
y = c2d(ds,1);
% 或 y = c2d(ds,1,'zoh');

后向差分法 + 前向差分法 + 双线性变换法

自定义函数c2d1，可以实现后向差分 + 前向差分 + 双线性变换
将下面的代码保存为 c2d1.m文件：

function y=c2d1(ds,t0,str)
% 函数 c2d1 补充MATLAB控制类函数 c2d 之不足,可以将连续传递函数以向前差分法和向后差分法变换为离散传递函数
% 因为双线性变换法与向前差分法和向后差分法同属近似法,所以 c2d1 函数也包括了双线性变换法
% 输出参数       y ：    LTI模型,离散传递函数
% 输入参数      ds ：    LTI模型,连续传递函数
%               t0 ：    数值,采样时间
%              str ：    字符串,变换方法   backdiff=向后差分   fordiff=向前差分  tustin=双线性
syms z x;
% ---------检查采样时间Ts是否大于0
if t0<=0
   error('Ts<0 or Ts=0 unallowed');
end
% ---------根据输入的"方法",确定代入公式
if strcmp(str,'backdiff')
   s=(z-1)/(t0*z);
   string='coefficient of result of backward difference:';
   string1='zero-pole of result of backward difference:';
elseif strcmp(str,'fordiff')
   s=(z-1)/t0;
   string='coefficient of result of forward difference:';
   string1='zero-pole of result of forward difference:';
elseif strcmp(str,'tustin')
   s=(2/t0)*((z-1)/(z+1));
   string='coefficient of result of double linear:';
   string1='zero-pole of result of double linear:';
else
   disp(' ');
   error('please chek method parameter');
end
% ---------%以下将模型的传递函数转换为符号表达式,以便s=f(z)代入到ds中
[num,den]=tfdata(ds,'v'); 	%取模型连续传递函数的分子和分母(多项式)
nums=poly2sym(num,x);	%将多项式转换为符号
dens=poly2sym(den,x);
tran=nums/dens; 	%生成一个符号分式
m=compose(tran,s); 	%代入
m=simplify(m); 	%化简

[n,d]=numden(m); 	%取符号表达式的分子和分母
n=sym2poly(n); 	%取符号表达式的分子多项式系数，按降幂排列
d=sym2poly(d); 	%取符号表达式的分母多项式系数，按降幂排列
% ---------%以下显示分子和分母的系数,是辅助性的
disp(string)
n=n/d(1); 	%使分母的最高项的系数为1
d=d/d(1);
n_str=num2str(n);
d_str=num2str(d);
n_disp=strcat('fn   =   ',n_str);
d_disp=strcat('fd   =   ',d_str);
disp(n_disp);
disp(d_disp);
% ---------%以下生成离散传递函数
y=tf(n,d,t0);
% ---------%以下求出离散传递函数的零点和极点
disp(string1);
[z,p,k]=zpkdata(y,'v')
% ---------%以下画出连续传递函数和离散传递函数的伯德图
% bode(ds,'r',y,'g'); % 如果需要画出Bode图可以加上这行代码
% zpk(z,p,k,t0)
% 程序结束

调用方法：

后向差分

% 在命令行输入：
y=c2d1(tf(1,[1 1 0]),1,'backdiff')
% c2d1(ds,t0,str)，其中ds = tf(1,[1 1 0])，t0 = 1，str = 'backdiff'

在这里插入图片描述

前向差分

% 在命令行输入：
y=c2d1(tf(1,[1 1 0]),1,'fordiff')
% c2d1(ds,t0,str)，其中ds = tf(1,[1 1 0])，t0 = 1，str = 'fordiff'

在这里插入图片描述

双线性变换

% 在命令行输入：
y=c2d1(tf(1,[1 1 0]),1,'tustin')
% c2d1(ds,t0,str)，其中ds = tf(1,[1 1 0])，t0 = 1，str = 'tustin'

在这里插入图片描述

双线性变换法

ds = tf(1,[1 1 0]);
y = c2d(ds,1,'tustin');

零极点匹配法

ds = tf(1,[1 1 0]);
y = c2d(ds,1,'matched');

最小拍无差控制系统设计

在这里插入图片描述

Gp = input('Gp='); % 输入被控对象传递函数
m = input('m='); % 输入m，阶跃输入：m=1；单位速度输入：m=2；单位加速度输入：m=3
Ts = input('Ts='); % 输入采样周期
Gz = c2d(Gp,Ts); % 广义对象的Z传递函数
G = zpk(Gz); % 化为零极点形式
z = tf('z');
fai_e = (1-z^(-1))^(m);
fai = 1-fai_e;
D = fai/(fai_e*G);
Dz = minreal(zpk(Dz)) % 得到最简零极点式

在这里插入图片描述

快速有纹波系统设计

将Gz写成z^-1形式：
在这里插入图片描述

Ts = 0.025;
Gp = tf(10,[0.025 1 0]);
Gz = c2d(Gp,Ts);
[a,b,k] = zpkdata(Gz);
Gz = zpk(a,b,k,Ts,'variable','z^-1')

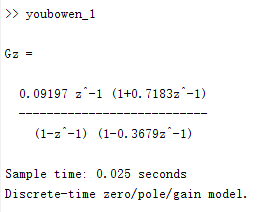
在这里插入图片描述
可以看出： $l = 1, w = 0, v = 1 (k = 1)$

Dahlin算法

在这里插入图片描述

%Delay Control with Dalin Algorithm
ts = input('ts=');
sys1 = input('G(s)=');
T_tao = input('T_tao=');
tao = input('tao=');
% Plant  控制对象传函:G(z)
Gz = c2d(sys1,ts,'zoh')
%Ideal closed loop  理想闭环脉冲传函:fi(z)
sys2=tf(1,[T_tao,1],'inputdelay',tao);
fai_z=c2d(sys2,ts,'zoh')
%Design Dalin controller控制器函数:D(z)
num = zpk(fai_z);
den = zpk(Gz*(1-fai_z));
nums = minreal(num)
dens = minreal(den)
% Dz = nums/dens 但由于dens部分含有延迟环节，无法使用'/'

在这里插入图片描述

则控制器: $D (z) = n u m s / d e n s$

Chapter 5

能控性与能观性判别

能控性

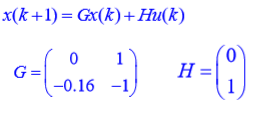
在这里插入图片描述

A = input('A=');
B = input('B=');
CONT = ctrb(A,B)
m = rank(CONT);
n = rank(A);
if m==n
    disp('系统状态可控')
else
    disp('系统状态不可控')
end

在这里插入图片描述

能观性

A = input('A=');
C = input('C=');
OBSER = obsv(A,C)
m = rank(OBSER);
n = rank(A);
if m==n
    disp('系统状态可观')
else
    disp('系统状态不可观')
end

状态反馈极点配置设计

在这里插入图片描述
首先要判断系统的状态可控性，若系统状态完全能控，可任意配置极点。

A = input('A=');
B = input('B=');
J = input('J=');
K = acker(A,B,J) % Ackerman法

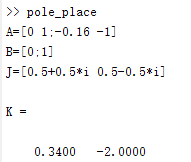
在这里插入图片描述

全维状态观测器设计

首先要判断系统的能观性，若能观，可以设计全维状态观测器。

全阶预报状态观测器

A = input('A=');
C = input('C=');
P = input('P=');
K = (acker(A',C',P))' % Ackerman法

在这里插入图片描述

全阶现时状态观测器

A = input('A=');
C = input('C=');
P = input('P=');
K = (acker(A',(C*A)',P))' % Ackerman法

基于状态空间模型的控制器设计实例

在这里插入图片描述
step 1：由传递函数G(s)写出连续状态空间方程：

step 2：连续状态空间方程的离散化
由Chapter 2中的连续状态方程离散化的MATLAB代码求得：

step 3：判断系统的能控性和能观性：
由Chapter 5中能控性与能观性判别的MATLAB代码可得：
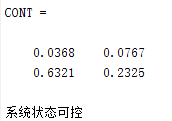
在这里插入图片描述

step 4：状态反馈极点配置
由Chapter 5中状态反馈极点配置设计的MATLAB代码可得：

step 5：设计状态观测器
由Chapter 5中全维状态观测器设计的MATLAB代码（此题为设计现今维）可得：

step 6：组成控制器

参考文献
[1] https://blog.csdn.net/weixin_42657460/article/details/106384556
[2] https://blog.csdn.net/weixin_44044411/article/details/86475605

Olefine1999

关注

4
点赞
踩
30

收藏

觉得还不错? 一键收藏
0
评论
《计算机控制理论与应用》MATLAB示例

S变换与Z变换MATLAB函数：例1：求 1s(s+1)\frac{1}{s(s+1)}s(s+1)1 的Z变换hc = tf(1,[1,1,0]);hd = c2d(hc,1,'imp'); % Ts = 1,'imp'表示脉冲响应不变法，即直接z变换结果如图：例2：含零阶保持器MATLAB程序中令K = 1：hc = tf(1,[1,1,0]);hd = c2d(hc,1); % Ts = 1, method 默认为‘zoh’结果如图：...
复制链接

扫一扫