正态分布性质

最新推荐文章于 2025-03-17 21:22:08 发布

基督徒Isaac

最新推荐文章于 2025-03-17 21:22:08 发布

阅读量2w

点赞数 17

文章标签：概率论机器学习逻辑回归

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/weixin_42683052/article/details/106907631

版权

两个高斯分布的和的分布——正态分布的再生性 - rainbow70626 - 博客园
https://www.cnblogs.com/rainbow70626/p/14070413.html

两个独立的正态分布的加法：

$N(\mu, \delta^{2} )+a \sim N(\mu+a,\delta^{2})$

$N(\mu,\delta_1^{2})+N(\mu,\delta_2^{2}) \sim N(u,(\delta_1^2+\delta_2^2))$

举例：

$N(0,1)+1 \sim N(1,1)$

$N(0,1)+N(1,1)-1 \sim N(0,2)$

（1）正态随机变量的线性函数仍为正态随机变量。

（2）正态随机变量的线性组合仍为正态随机变量。

（3）正态随机变量的乘积仍为正态随机变量。

直觉中，两个高斯（正态）随机变量的和似乎应该是两个概率密度函数的和，如下图所示，其结果就近似为两个概率密度的包络线，这明显是错误的，是用直觉推导数学，大错特错。

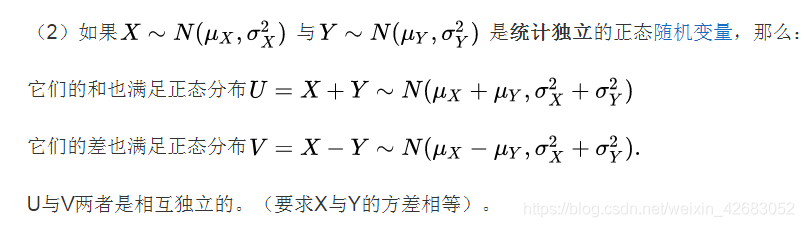
t分布、二项分布、Poisson分布的极限为正态分布，在一定条件下，可以按正态分布原理来处理。

评论 1

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。