1.单应性矩阵是什么?
言简意赅定义:定义在两个不同视角中对同一平面范围内的特征点的射影变换(projective transformation)即:
x1 = H*x2 //x1、x2为匹配点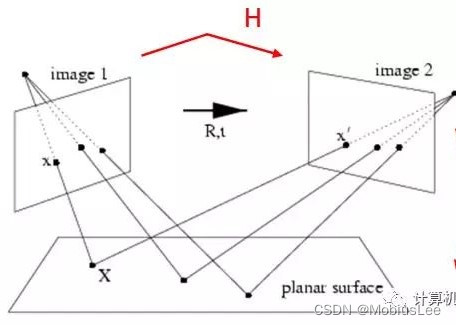
上图中x,x‘为一对匹配点,通过单应矩阵H实现在各自图像坐标系下的坐标转化。
H矩阵(单应性矩阵)大小为3×3:
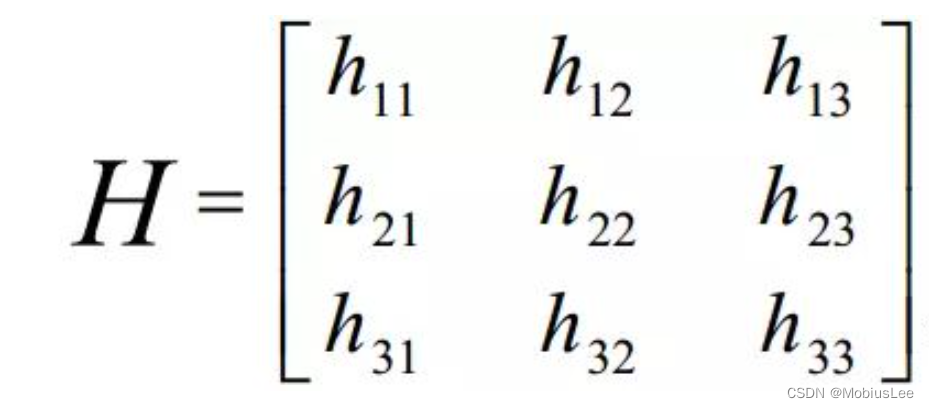
因为H矩阵因尺度一致性,减少一个自由度,故H矩阵的自由度为8(有疑问可网上搜索一下),因此我们有两种处理方法:
1.可以将 h33 设置成1
2.或者||H|| = 1,即:
![]()
2.单应矩阵求解原理
故在两视角所有匹配点对都满足:
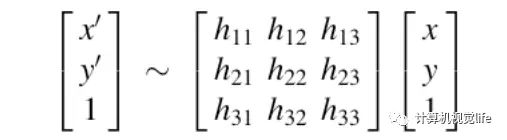
进而变换为:
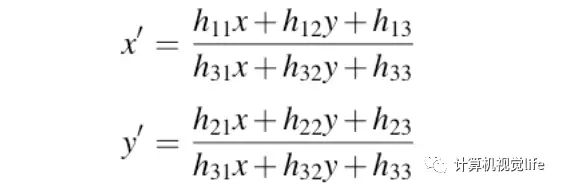
进而转化为:
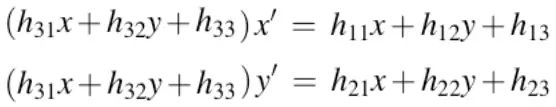
进而转化为:
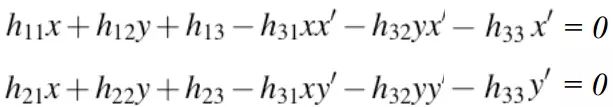
假如我们得到了两幅图片中对应的N个点对(特征点匹配对),那么可以得到如下线性方程组:

写成矩阵形式:
![]()
由于单应矩阵H包含了||H||=1约束,因此根据上图的线性方程组,8自由度的H我们至少需要4对对应的点才能计算出单应矩阵。但是,以上只是理论推导,在真实的应用场景中,我们计算的点对中都会包含噪声。比如点的位置偏差几个像素,甚至出现特征点对误匹配的现象,如果只使用4个点对来计算单应矩阵,那会出现很大的误差。因此,为了使得计算更精确,一般都会使用远大于4个点对来计算单应矩阵。另外上述方程组采用直接线性解法通常很难得到最优解,所以实际使用中一般会用其他优化方法,如RANSAC算法、奇异值分解、Levenberg-Marquarat(LM)算法(后续文章会介绍)等进行求解。
3.单应矩阵用于摄像机标定
我们标定其实就是从单应矩阵H中恢复出内外参数矩阵,怎么理解标定里面H?因为我们常常把标定的棋盘格图像放在平面上,并设定Z=0,故棋盘格自身是一平面xy坐标系,而最后我们摄像机的像素坐标系也可看作一个xy坐标系,那么这就符合单应矩阵的使用情景可用于求解两坐标系中匹配点对的映射变换关系。详见从零开始学习「张氏相机标定法」(一)
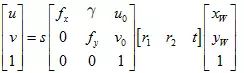
其中,u、v表示像素坐标系中的坐标,s表示尺度因子(等于1/zw),fx、fy、u0、v0、γ(由于制造误差产生的两个坐标轴偏斜参数,通常很小)表示5个相机内参,R(对应列向量r1、r2、r3),t表示相机外参,xw、yw、zw(zw= 0,上面公式未写出,其中 1 是齐次化表达的最后一维)(假设标定棋盘位于世界坐标系中Zw=0的平面)表示世界坐标系中的坐标。故我们这里把内外参合并看作H。
r3,zw没写出是因为r3*zw=0,故可以同时省略。

流程:
1、打印一张棋盘格标定图纸,将其贴在平面物体的表面。
2、拍摄一组不同方向棋盘格的图片,可以通过移动相机来实现,也可以移动标定图片来实现。
3、对于每张拍摄的棋盘图片,检测图片中所有棋盘格的特征点(角点,也就是下图中黑白棋盘交叉点,中间品红色的圆圈内就是一个角点)。我们定义打印的棋盘图纸位于世界坐标系Zw=0的平面上,世界坐标系的原点位于棋盘图纸的固定一角(比如下图中黄色点),像素坐标系原点位于图片左上角。
4、因为棋盘标定图纸中所有角点的空间坐标是已知的,这些角点对应在拍摄的标定图片中的角点的像素坐标也是已知的,如果我们得到这样的N>=4个匹配点对(越多计算结果越鲁棒),就可以根据LM等优化方法得到其单应矩阵H。当然计算单应矩阵一般不需要自己写函数实现,OpenCV中就有现成的函数可以调用。现在也有专门用于传感器标定的工具箱Kalibr(github链接),精度要好于OpenCV。
4.单应矩阵恢复内外参数学推导
我们知道H是内参矩阵和外参矩阵的乘积,而我们想要最终分别获得内参和外参。所以需要想个办法,先把内参求出来(先求内参是因为更容易),得到内参后,外参也就随之解出了。
我们先不考虑镜头畸变(正规的标定是包含镜头畸变的),来看看如何求解内参和外参。求解思路是利用旋转向量的约束关系,以下是具体推导,建议自己演算一遍,加深理解。
为了利用旋转向量之间的约束关系,我们先将单应性矩阵H化为3个列向量,即H=[h1 h2 h3],则有:
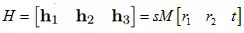
进而转换为:
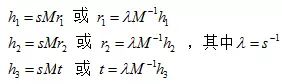
因为旋转向量在构造中是相互正交的,即r1和r2相互正交,由此我们就可以利用“正交”的两个含义,得出每个单应矩阵提供的两个约束条件:
约束条件1:旋转向量点积为0(两垂直平面上的旋转向量互相垂直),即:
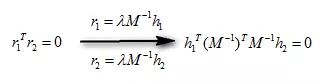
约束条件2:旋转向量长度相等(旋转不改变尺度),即:
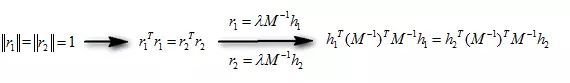
所以一个单应性矩阵H可以提供上述两个约束条件。那么如何利用上述两个约束条件求解内参或者外参呢?我们一步一步来看,由前面可知内参矩阵M:
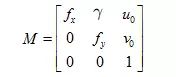
利用M定义B:
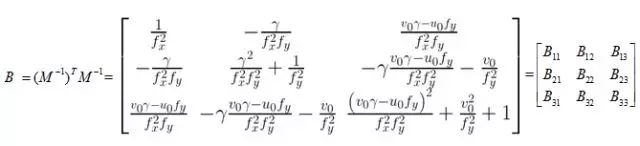
我们看到B为对称矩阵,真正有用的元素只有6个(主对角线任意一侧的6个元素)。把B带入前面两个约束条件后可转化为:
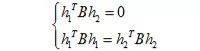
上面两约束中的式子均可写为通式:
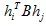
的形式,定义3X3的单应矩阵H=[h1 h2 h3]的第i列列向量:
![]()
将如下表达式代入上述的约束单项式:
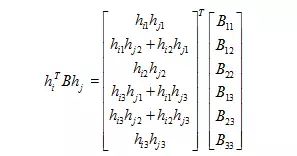
其中,令:
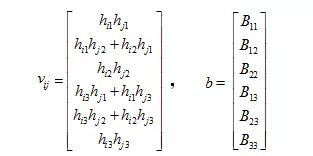
则:
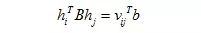
由此,两约束条件最终可以转化为如下形式:

假设我们已经根据前面计算得到了矩阵B元素的值,那么根据已知的矩阵B很容易解出内参,如下:
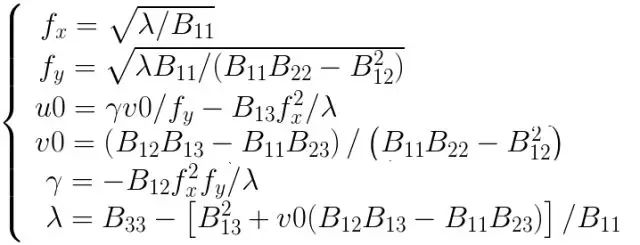
得到内参数后,内参矩阵M也已知。单应矩阵H也已知,因此可继续求得外参数:

其中又由旋转矩阵性质有:
![]()
则:
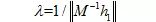
实际情况下,数据中是存在噪音的,所以计算得到的旋转矩阵R并不一定能满足旋转矩阵的性质。所以通常根据奇异值分解来得到旋转矩阵R。
5.补充
上述的推导结果是基于理想情况下的解,从理论上证明了张氏标定算法的可行性。但在实际标定过程中,一般使用非线性优化求解。假设我们拍摄了n张标定图片,每张图片里有m个棋盘格角点。三维空间点X在图片上对应的二维像素为x,三维空间点经过相机内参M,外参R,t变换后得到的二维像素为x',假设噪声是独立同分布的,求解上述非线性优化问题得到最小化x, x'的位置来:
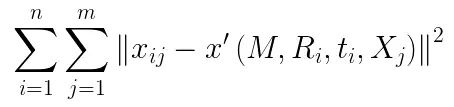
现在我们来考虑透镜畸变的影响,由于径向畸变的影响相对较明显,所以主要考虑径向畸变参数,根据经验,通常只考虑径向畸变的前两个参数k1,k2就可以(增加更多的参数会使得模型变的复杂且不稳定)。实际求解中,通常把k1,k2也作为参数加入上述函数一起进行优化,待优化函数如下所示:
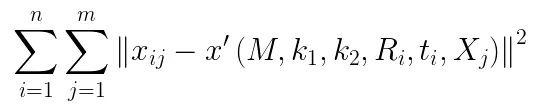
上述非线性优化问题通常用Levenberg-Marquardt(LM)算法进行迭代求解。一般将k1,k2初值设为0。






















 893
893











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








