【论文笔记】ST-GAT A Spatio-Temporal Graph Attention Network for Accurate Traffic Speed Prediction

ST-GAT A Spatio-Temporal Graph Attention Network for Accurate Traffic Speed Prediction

摘要

整合GNN和RNN的时空模型目前已经在交通速度预测方面取得了很好的准确率，但其时间依赖和空间依赖是独立在两个维度的，不能利用时间和空间上的联合依赖性。

该文章中，考虑了两种速度的个体在时空可能点上的依赖关系，以准确预测交通速度。

文章提出了IST-graph以表现个体时空依赖，以及一个基于IST-graph和注意力机制的新模型ST-GAT，来预测未来的交通速度。

在5个真实数据集上展示的效果：

• IST-graph在对交通速度数据进行建模时有效；
• ST-GAT在预测准确率上超过了5个目前最好的模型；
• 在异常交通场景下，ST-GAT鲁棒性较好。

介绍

当前很多提出的交通速度预测模型都同步考虑时间依赖和空间依赖，如RNN (LSTM, GRU)用于时间依赖，GNN、GCN等模型被用于空间依赖。

DMSTGCN学习潜在空间依赖并将空间和时间依赖独立考虑，STSGCN在本地以及小时间窗口下，部分考虑了时间与空间的联合依赖。但他们都没有考虑所有可能个体的时空依赖。

(a)图展示了当前模型预测交通速度的方法，其采用了循序渐进的方法，将时间点$i$的$A_i,B_i,C_i$整合进入$D_i$（整合空间依赖），然后将$D_i$的信息整合进$D_p$中（整合时间依赖）。其实就是先整合空间依赖，再整合时间依赖，有序。

但是，如果有很多车辆在$A_i,B_i,C_i$并且在单位时间后，$D_i$向$D_p$移动，就会从$A_i,B_i,C_i,D_i$到$D_p$出现个体时空依赖。

IST图及ST-GAT模型

为了解决这个局限，文章提出了IST-graph来代表IST依赖，以及ST-GAT模型来预测交通速度。

IST图用$<segment,timepoint>$对作为一个结点（segment就是指上文的$A_i,B_i,etc.$），将结点对的IST依赖作为一条有向边。这样，IST图就能代表所有可能的个体时空依赖。

一个特定时间点的特定segment被称为ST-point，一组ST-point被表示为IST图，每个$<s,t>$的ST-point都有速度属性$x$。

我们假设ST-point间所有可能的IST依赖都存在，仅除了时序颠倒的情况。

自注意力机制

为了获得准确的ST-point嵌入，文章使用了自注意力机制来学习ST-point间的隐藏IST依赖，从而使得ST-point能够被嵌入地更加准确。

基于5个真实数据集的实验显示，文章提出的模型能比当前最优模型准确率提高2%-33%。

Motivation

文章使用了ST-point点对5分钟单位下的两个交通速度序列Pearson相关系数，从而检测METR-LA数据集是否存在IST依赖。

图2是METR-LA随机抽取一段时间的热力图结果，图中每格代表ST-point的$<x,y>$，格子颜色代表相关系数。

从图像结果可以看出，个体相关性并不局限于pivot附近时空的其他ST-point间，而是分布于整个时空当中。从图中可以看出，即使pivot时间发生改变，一个segment的同一ST-point仍然会不断出现强相关。

由于所有ST-point都有与pivot存在相对的时空差异，这些相关的重复pattern表明pivot的交通速度与ST-point间IST依赖的存在。

思路

IST图

空间图将一个路网片段作为结点，并把空间依赖作为两个segment的边。但是其仅能表示空间依赖。

IST图是一个有权有向图，一个结点代表一个ST-point，一条边代表一对ST-point的IST依赖，边的权重代表IST依赖的强弱，ST-point中包含交通速度属性。在模型中，边的权重是可学习的；边的方向与时间流的方向相同，在同一时间点、不同片段间可能存在双向边（空间图中车流可能是双向的）。

在存在$m$个片段，$\alpha$个时间步（上文中，1个时间步为5分钟）下，IST图$G$可以形式化地表示为：
G = { V , E , X } { V = { v s t ∣ v 11 , … , v 1 α , … , v m 1 , … , v m α }   ( n o d e s ) E = { v i j → v k l , w h e r e   j ≤ l }   ( e d g e s ) X = { x v 11 , … , x v m α }   ( a t t r i b u t e s ) G=\{V,E,X\} \left\{ \begin{array}{lr} V=\{v_{st}|v_{11},\dots,v_{1\alpha},\dots,v_{m1},\dots,v_{m\alpha}\}\ (nodes)\\E=\{v_{ij}\rightarrow v_{kl},where\ j\leq l\}\ (edges)\\X=\{x_{v_{11},\dots,x_{v_{m\alpha}}}\}\ (attributes) \end{array} \right. G={V,E,X}⎩⎨⎧​V={vst​∣v11​,…,v1α​,…,vm1​,…,vmα​} (nodes)E={vij​→vkl​,where j≤l} (edges)X={xv11​,…,xvmα​​​} (attributes)​

时空图注意力机制

为防止对IST依赖的平滑，文章采用了注意力机制以学习IST依赖的度（degree）。

ST-GAT分为两个block：

• 嵌入块（embedding block）：通过对IST依赖（edge）的学习来将ST-point（node）投影到嵌入空间的向量中；
• 预测块（prediction block）：用于预测每个片段$\beta$时间步下的交通速度。

Embedding Block

在IST图$G$有$m$个片段，$\alpha$个时间步情况下，对于第$i$个ST-point $e{m}_i$有形式化表达：
$$e{m}_i=\sigma (att({\hat{x}}_i)),where{\hat{x}}_i=\sigma (x_i{W}_i)\in {\mathbb{R}}^{d_1}$$
其中，$d_1$表示用户定义的维度，$W_i$代表第$i$个ST-point的可学习权重参数。对每个ST-point的注意力机制可被表示为：
$$att({\hat{x}}_i)=\sum _{j\in n_i}{a}_{ij}{\hat{x}}_j{W}^V$$
其中，$n_i$是第$i$个ST-point的邻居集合，$a_{ij}$是第$i$和第$j$个ST-point间的注意力分数（Softmax）：
$$a_{ij}=\frac{exp(edg{e}_{ij})}{{\sum }_{k\in n_i}exp(edg{e}_{ik})}$$
其中，$edg{e}_{ij}$是IST依赖的度：
$$edg{e}_{ij}=\frac{{\hat{x}}_i{W}^Q({\hat{x}}_j{W}^K{)}^T}{\sqrt{d_x}}$$
其中，$W^Q,W^K,W^V$是query、key、value的可学习参数，$d_x$代表交通速度$x$的维度。

通过注意力机制，IST依赖的度是个体决定的，这使得ST-GAT可以成功学习到ST-point间IST依赖的个体模式。

Prediction Block

在预测块中，$\beta$时间步，$m$片段下的交通速度预测值$\hat{Y}$可以被形式化地表示为：

$$\begin{gathered} {\hat{Y}}_i=\sigma ({\mathbb{T}}_i{W}^{P_i}+b^{P_1})W^{P_2}+b^{P_2},where\{\begin{array}{l}{W}^{P_1}\in {\mathbb{R}}^{d_1\times d_2}\\ W^{P_2}\in {\mathbb{R}}^{d_2\times \beta }\end{array} \\ {\mathbb{T}}_i=\widehat{e{m}_i}\odot {\widehat{em}}_{m+1}\odot \cdots \odot {\widehat{em}}_{i+\alpha -1} \\ {\widehat{em}}_i=e{m}_i+\sigma (e{m}_i{W}^R+b^R),where{W}^R\in {\mathbb{R}}^{d_1\times d_1} \end{gathered}$$

其中，$\mathbb{T}\in {\mathbb{R}}^{d_{em}\times \alpha }$是每个片段$\alpha$时间步下的ST-point嵌入，$\odot$表示concat操作，$W^{P_1}$和$W^{P_2}$表示全连接层的可学习参数，$d_2$代表$W^{P_1}$的维度，$W^R$代表残差层中的可学习参数。

ST-GAT采用端到端的训练方式，损失函数可以表示为：
L ( W θ ) = 1 m × β ∑ i ∈ m ∣ Y i − Y ^ i ∣ , w h e r e   W θ = { W Q , W K , W V , W P 1 , W P 2 , W R } L(W_\theta)=\frac{1}{m\times \beta}\sum_{i\in m}|Y_i-\hat{Y}_i|,where\ W_\theta=\{W^Q,W^K,W^V,W^{P_1},W^{P_2},W^R\} L(Wθ​)=m×β1​i∈m∑​∣Yi​−Y^i​∣,where Wθ​={WQ,WK,WV,WP1​,WP2​,WR}

评估

实验设置

所用数据集：

• METR-LA
• PeMS-{Bay, M, D4, D8}

Baseline：

• STGCN
• AGCRN
• STSGCN
• DMSTGCN
• GMAN

指标：

• MAE
• RMSE
• MAPE

实验结果

IST图的有效性

GCN和GC-GRU模型在使用IST图的情况下，较使用空间图的情况，精确率提高了6%-13%。

与最优模型间的精确率比较

• 尝试获得道路网络中潜在连接的模型（AGCRN、STSGCN、DMSTGCN、GMAN、ST-GAT）精确率都比仅使用物理连接的STGCN更高；
• 在使用潜在连接的模型中，基于注意力机制的模型（GMAN、ST-GAT）精确率比基于GCN的模型更高；
• ST-GAT表现最好，除了使用PeMS-D8数据集的GMAN。

模型训练

在ST-GAT中，输入的IST图大小是空间图的$\alpha$倍，但其可通过一层注意力网络学习到所有IST依赖，因为所有的ST-point都被连接在一跳之内。

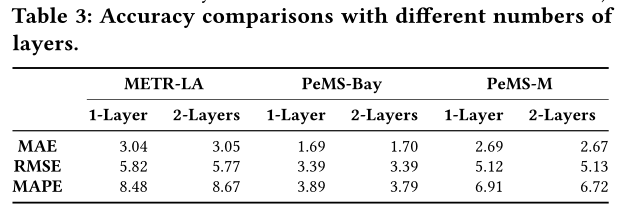
不同注意力网络层数下，误差没有显著差异。

案例研究

ST-GAT效果最好，特别是在对高峰时段交通速度快速/突变情况下的结果，ST-GAT表现最好。这表明ST-GAT在异常情况下速度预测的鲁棒性更好。

拓展内容

Pearson系数

注意力机制

https://blog.csdn.net/qq_37492509/article/details/114991482