机器学习的数学基础（6）：矩阵的SVD分解与最小二范数解

其实在上一篇文章中遗留了两个问题。在我们讨论最小二乘回归问题解的时候，当rank(A)<min(M,N)时，问题有二：1. 解的形式为其中为标准方程的解，在非满秩的情况下如何求得此时标准方程的一个解。2. 此时问题有无穷个解，我们应如何对这无穷个解进行选择。

解决上述问题，我们需要用到一个重要的数学工具: SVD

一. 奇异值分解（SVD）：

奇异值分解描述如下：

一个任意的矩阵A（M,N），rank(A)=R，可以被分解为如下的形式：

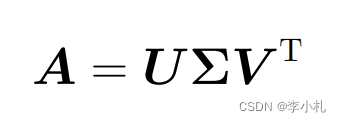
其中：

1. U是一个M*R维度的矩阵，且满足：

不难看出，因为是一个M*M的方阵，因此可以对其做特征值分解， 中的元素自然也是所对应的特征值，且U可以被表示为：

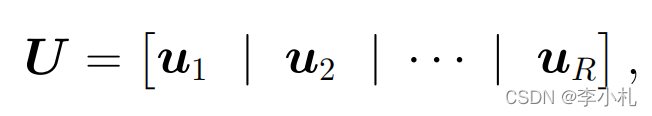
 为U的特征向量。

2. V是一个N*R维度的矩阵，且满足：

 同样的方式，我们表示出V，V为所对应特征值分解的向量：

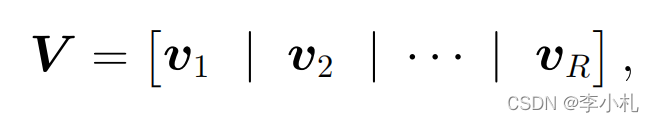
此外 和所对应的特征值是相同的。

3. 则是矩阵A所对应的奇异值矩阵，是一个对角阵，满足：

矩阵中对角线上的元素均为矩阵A的奇异值，并且有先前的推导我们知道，奇异值实际上是 和所对应的特征值的开方。

单从工程的角度求解奇异值，我认为以上的几个概念就够了，但是为了后续的数学推导做铺垫，我们还需要再度提及一些概念：

4. 当R<M时，矩阵存在非平凡零空间，并且这个零空间我们可以表示为一组正交基底张成的空间如下：

其中  

5. 当R<N时，矩阵存在非平凡零空间，并且这个零空间我们可以表示为一组正交基底张成的空间如下：

其中： 

铺垫做完了，接下来开始回答文中一开始所提出的问题。

二. 最小二乘的最小二范数解

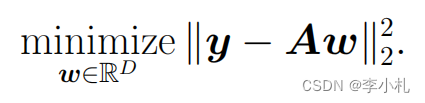
对于上面的问题，当rank(A)<min(M,N)时，该问题存在无穷解，因此我们需要一种约束来挑选无穷个解中的其中一个作为我们的解，其中的一种挑选规则就是我们在所有解中挑选出具有最小二范数的解，建模如下：

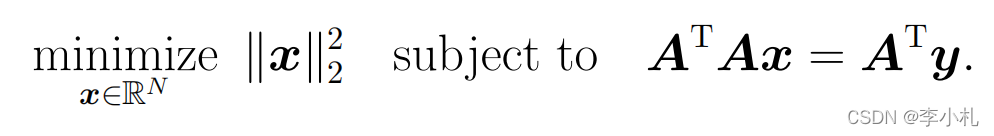
求解上述的优化问题，我们则需要用到SVD。

首先对A进行SVD分解，我们有：

先说结论，最终解可以被表示为如下形式：

其中前一项为，后一项为v（A零空间中的元素）。而为了保证x的二范数最小，后一项v应为0，所以上述问题的解为

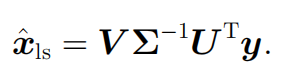
而我们把称之为矩阵A的伪逆

证明：

任何一个属于空间的向量都可以被我们表示为：

这是因为V与V0的列向量为一组相互正交的向量且数量为n，因此V与V0的列向量张成的空间为

并且由特征向量的性质我们有如下的关系：

 镜像的我们对y也做同样的操作：

联立上述四个等式，我们有如下的推导：

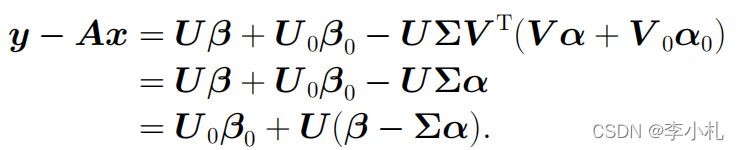
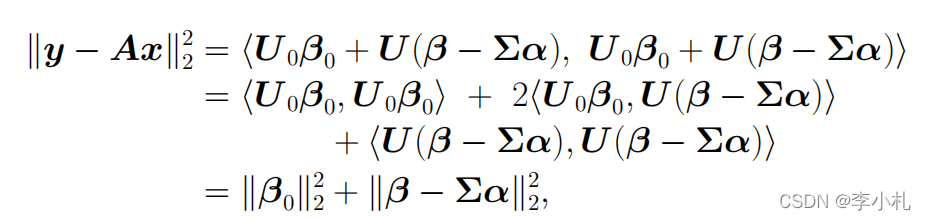
那么最小二乘问题可以被我们表示为：

这里只要解出来，带入即可求出x。

那么因为这一项是与y有关的，是一个常量，因此想让这个表达式最小，我们只需要做到

显然是可逆的，因此我们可以解出 ：

 而为了保证x的二范数最小，后一项v应为0，所以上述问题的解为

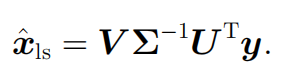
得证！