不同维度的矩阵相乘的维度结果（高维数组相乘的运算规则）、时间复杂度计算

一、高维数组相乘的运算规则

相乘必须满足以下两个条件：

1. 两个n维数组的前n-2维必须完全相同。例如（3,2,4,2）（3,2,2,3）前两维必须完全一致；
2. 最后两维必须满足二阶矩阵乘法要求。例如（3,2,4,2）（3,2,2,3）的后两维可视为（4,2）x（2,3）满足矩阵乘法。

这样的同维矩阵相乘，所得到的维度是：前n-2维不变，后2维进行矩阵乘法。

例如，（3,2,4,2）*（1,2,2,3）——>>（3,2，4,3）

高维数组相乘的运算规则_两个维度相同的方阵相乘的维度-CSDN博客

 二、时间复杂度计算

 一张图就明白了: 

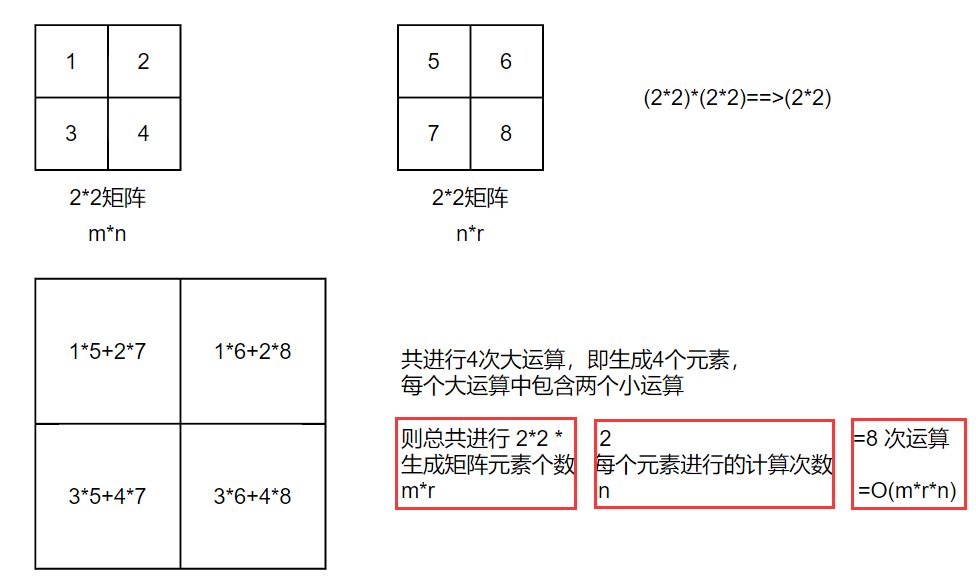
关于转置矩阵

二个矩阵乘法

对于矩阵A(n*m),B(m*n), 这里A(n*m)表示A是n行乘m列的矩阵。

如果A*B，那么复杂度为O(n*m*n),即O(n^2m) 。进一步思考，为什么呢，直接代码解释：

 for(i=0;i<n;i++){ //A矩阵中的n
        for(j=0;j<m;j++){  //A矩阵中的m 或者B矩阵中的m ,一样的
            for(k=0;k<n;k++){ //B矩阵中的n
                C[i][j]= C[i][j]+A[i][k]*B[k][j]; 
             } 
         } 
     }

一个for循环是O(n),这里是三个for循环，所以为O(n*m*n)。（ps：个人感觉还是看代码比较好理解，后面三个矩阵乘法时，就会更加体会到）

三个矩阵乘法

对于矩阵A(m*n),B(n*m)和C(m*n),  这里A(m*n)表示A是m行乘n列的矩阵。

• A*B，那么复杂度为O(m*n*m),即O(m^2n) 。
• D(m*m)=A*B运算完后在和C运算。
• D*C,那么复杂度为O(m*m*n),即O(m^2n) 。

与(A*B)*C等价。整个过程算法复杂度为O(m^2n) 。（一开始笔者以为是O(m^2n)*O(m^2n) = O(m^4n^2), 其实这样理解是错的，下面介绍）