osqp论文解读(一)

An Operator Splitting Solver for - Quadratic Programs

OSQP 一种对二次规划问题的裂算子解算器

前言

基于ADMM方法，我们提出了一种对于凸二次规划的通用方法解算器，采用了一种新颖的算子拆分技术，该技术需要在几乎每次迭代中求解具有相同系数矩阵的准定(quasi-definite)线性系统。该算法鲁棒性好，对要解决问题的数据机会没有要求，比如一般算法都要求的目标函数的正定性，约束函数的线性无关性。一旦执行初始矩阵分解，通过可以配置即可实现无除法，使其适用于嵌入式系统中的实时应用。此外，该技术是第一个能够从算法迭代中可靠地检测原始问题和对偶问题不可行的二次规划的算子拆分方法。该方法还支持因式缓存分解和热启动，使其在解决经济、控制和机器学习中出现的参数化问题时特别有效。我们的开源 C 代码实现 - OSQP 占用空间小，无需额外的库，并且已经在来自各种应用领域的许多问题实例上广泛测试。它通常比使用的内点法的其他解算器快十倍，有时在使用因式分解缓存或热启动的情况下，甚至要快得多。OSQP已经在学术界和大公司中对数以万计的用户产生了巨大的影响。

介绍

问题描述

考虑以下优化问题：

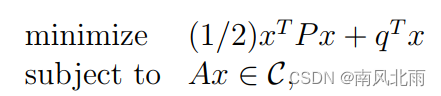
式中，x是决策变量，目标函数由半正定矩阵P和向量q定义，A是约束矩阵，C是非空闭凸集。
此类问题，饿哦们也通常叫做，普通(凸)二次规划问题。
如果结合C采用以下方式来表达：

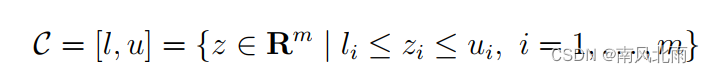
如果li和ui都满足

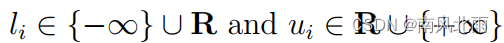
我们就可以把问题重新写成以下方式

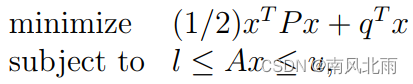
这也就是我们通常所指的二次规划。如果遇到线性等式约束，我们可以用通过将对应的li =ui的方式添加。 注意，对于线性规划问题，我们都可以通过将P=0的方式得到。我们将以上优化问题的大小归用元组(n, m, N)表示，N是矩阵P A中非零个数之和。N =nnz§ + nnz(A)。

应用

以上优化问题出现在工程、金融、运筹学和许多其他领域的各种应用中。如SVM，LASSO，拟合，金融上的投资组合，控制上的MPC，MHE，而且要求短时间内求解QP问题。同时QP子问题的数值解也是非凸优化问题的重要部分如序列二次优化和混合整数优化。

解方法

从1950年人们就开始研究凸二次规划问题，继Kantorovich 发起的开创性的LP解法工作之后。LP 和 QP 的几种解决方案具有多年来一直被提出和改进。
有效集法(Active-set method)
该方法是第一个作为解决方案推广的算法QP 的方法，并且是起源于 Dantzig 的单纯形方法。算法选择一个激活集（即一组绑定约束），然后通过在索引中添加和删除约束来迭代调整它。根据成本函数梯度和当前对偶变量添加新的激活约束。QP 的激活集方法与 LP 的单纯形方法不同，因为迭代不一定是可行区域的顶点。该方法可以很容易地热启动，以减少所需的激活集重新计算的次数。然而，激活集方法的主要缺点是，最坏情况的复杂性随着约束数量的增加呈指数级增长，因为在达到最佳约束之前，可能需要研究所有可能的激活集。在许多商业求解器中都使用激活集方法来求解 QP 问题，例如MOSEK 和 GUROBI 以及开源求解器 qpOASES。
内点法(Interior-point methods)
内点算法在 1980 年代作为一种在多项式时间(polynomial time)内求解 LP 的方法而流行起来。在90年代，这些技术扩展到了普通的凸优化问题，包括QP问题。内点法把问题的约束视为带参的惩罚函数，也成为障碍函数。通过求解无约束问题过程中每次迭代都改变障碍函数的参数，来达到最优值。原始-对偶内点法，也就是Mehrotra predictor-corrector法因为实际引用中的良好性能成为不二选择。然而，内点方法不容易热启动，并且对于非常大的问题不能很好地扩展。内点法成为i一些商业软件中的默认方法如MOSEK， GUROBI，CVXGEN和开源OOQP。
一阶法(First-order methods)
一阶优化方法可以追溯到1950年代，这些方法仅使用有关成本函数的一阶信息迭代计算最优解。裂算子技术（如 Douglas-Rachford 法）是一类特殊的一阶方法，它将优化问题看作寻找单调算子之和的零点的问题。
近些年，裂算子法也叫ADMM方法因其较好的收敛性得到了广泛关注。ADMM可以看作是经典交替投影算法的变种，即寻找两个凸集的相交点，也就是所谓的DouglasRachford splitting。ADMM已被证明可以在相对较少的计算成本低廉的迭代中解决 QP，并可靠地提供适度的精度。它因此，非常适合嵌入式优化或大规模优化等应用，在这些应用中，由于数据中的噪声，通常不需要高精度解决方案以及成本函数的任意性。ADMM在计算上非常廉价且易于实现，因此非常适合计算资源有限的嵌入式处理器，例如嵌入式控制系统中的嵌入式处理器。ADMM还与分布式优化架构兼容，能够解决非常大规模的问题。
一阶方法的缺点是它们通常无法检测原始/或对偶不可行性。为了解决这一缺点，提出了一种与ADMM结合使用的齐次自对偶嵌入法，用于求解圆锥优化问题，并在开源求解器SCS中实现。虽然每个QP都可以被重新表述为圆锥程序，这种重新表述从计算中上来看效率不高。ADMM的另一个缺点是收敛所需的迭代次数高度依赖于问题数据和用户对算法步长参数的选择。尽管最近有一些理论结果，但仍然不清楚如何选择这些参数来优化算法收敛率。因此，尽管使用ADMM技术求解优化问题有许多好处，但依然没有基于裂算子的可靠通用QP求解器。
我们的方法
我们基于ADMM方法提出了一种新的能够提出高精度解的通用QP求解器，所提出的算法基于一种新颖的裂算子法来求解一个准定线性系统，且对于任何问题数据的选择都是可求解的。因此，我们没有施加任何约束，例如成本函数的严格凸性或约束的线性独立性。由于当 ρ 固定时，线性系统的矩阵系数在每次迭代中都保持不变，我们的算法只需一次因式分解就能解决QP问题。一旦计算出这个初始因式分解，我们就可以固定线性系统矩阵系数，使算法无除法。如果我们允许除法，那么我们可以视情况对这个线性系统中的项 ρ 进行更新，以提高算法的收敛性。我们发现在实验中算法通常很少更新这些系数。与其他一阶方法相比，我们的方法能够在问题可解时返回原始解和对偶解，或者在不诉诸齐次自对偶嵌入的情况下提供原始和双重不可行性的证明。为了获得高精度的解决方案，我们对从ADMM获得的迭代解进行打磨。通过从最终的对偶变量迭代中识别激活约束，我们构建了一个辅助相等约束 QP，其解等价于原始 QP 的解。然后，通过计算单个线性系统的解来解决这个辅助问题，该线性系统的维数通常比ADMM迭代期间求解的维度低得多。如果我们正确地识别了主动约束，那么我们方法的结果解的精度等于甚至优于内点方法。
我们的算法可以有效地热启动，以减少迭代次数。此外，如果问题矩阵没有变化，那么准定系统分解可以在多个求解中重复使用，从而大大缩短计算时间。此功能在求解参数化 QP 的多个实例时特别有用，其中问题数据中只有少数元素发生变化。举例说明拟议方案的有效性嵌入式应用中出现的参数化程序中的算法。我们在开源的 Operator Splitting Quadratic Program“（OSQP） 求解器中实现了我们的方法。OSQP 是用 C 语言编写的，可以编译为无库。OSQP 对嘈杂和不可靠的问题数据具有鲁棒性，代码占用空间非常小，适用于嵌入式和大规模应用。我们已经广泛测试了我们的代码，并通过求解数百万个 QP 仔细调整了其参数。我们将求解器与最先进的内点求解器和主动集求解器进行基准测试，该求解器包含来自 7 个不同类别的 1400 个问题的基准库，并基于硬 QP Maros-M’esz’aros 测试集。 数值结果表明，我们的算法能够比现有的商业和开源求解器提供高达一个数量级的计算时间改进， 且应用范围广泛。结果还显示通过从热启动，解算时间进一步减少，和能缓存分解。