观察性研究和混杂因素
观察性研究:根据经验观察推断因果作用的研究,但不能采用有控制的试验, 也不能随机地分配处理。
举个例子:
关于加利福尼亚大学伯克莱分校的研究生入学中是否存在性别歧视的研究. 他们在观测数据中发现男生录取比例高于女生, 但是, 根据学生申请专业分层后, 发现女生的录取率略高于男生. 可见, 如果没有记录学生的报考专业数据, 或者不对此做调整, 就会产生完全错误的结论. 在这个例子中, 申请专业是研究性别对录取率影响的关键因素, 称为混杂因素, 忽略这样的因素会导致因果作用估计的偏差。
判断和确定哪些变量或因素是混杂因素的问题是因果推断中最基本和关键的问题.
判断和确定哪些变量或因素是混杂因素的问题是因果推断中最基本和关键的问题.
判别混杂因素的准则大致分为两大类: 可压缩性准则和可比较性准则.
可压缩性准则根据相关关系的度量定义混杂因素. 如果相关关系的度量受第三个变量的影响, 那么该变量为混杂因素.
可比较性准则是基于潜在结果模型来定义混杂偏倚和混杂因素. 如果暴露总体的潜在结果
Y
1
Y_1
Y1和
Y
0
Y_0
Y0的分布分别与非暴露总体的潜在结果的分布相同,则称暴露总体与非暴露总体是可比较的 (或称可交换的), 也称为无混杂偏倚. 在这种情形下暴露对结果的平均因果作用
A
C
E
=
E
(
Y
1
)
−
E
(
Y
0
)
ACE=E(Y_1)-E(Y_0)
ACE=E(Y1)−E(Y0)等于暴露组与非暴露组观测结果的期望之差
E
(
Y
∣
X
=
1
)
−
E
(
Y
∣
X
=
0
)
E(Y|X=1)-E(Y|X=0)
E(Y∣X=1)−E(Y∣X=0)
混杂因素必须满足的两个条件
(1)
V
V
V是一个独立因素.
(2)
V
V
V在暴露总体与在非暴露总体中的分布不同.
可忽略性假定
可忽略性假定是观察性研究中判断混杂因素和推断因果作用最重要的假定.
(处理分配机制的可忽略性 (ignorability of treatment assignment mechanism)
令
V
V
V表示观测的协变量, 如果满足
(
i
)
(
Y
1
,
Y
0
)
∐
X
∣
V
和
(
i
i
)
0
<
p
r
(
X
=
1
∣
V
)
<
1
(i)(Y_1,Y_0) \coprod X|V和(ii)0<pr(X=1|V)<1
(i)(Y1,Y0)∐X∣V和(ii)0<pr(X=1∣V)<1那么称处理分配机制是可忽略的.
可忽略性假定中的条件
(
i
)
(i)
(i)相当于在
V
V
V 的每一层做了随机化分配, 那么, 在
V
V
V 的每一层, 平均因
果作用是可识别的, 进而对 V 求期望可以得到总体的平均因果作用. 条件
(
i
i
)
(ii)
(ii) 要求在
V
V
V 的每一层里
接受处理或对照的概率大于 0, 这是为了保证在每一层都能得到该层平均因果作用的相合估计. 在可忽略性假定下, 平均因果作用可通过以下公式识别:
E
(
Y
1
)
−
E
(
Y
0
)
=
E
[
E
(
Y
1
−
Y
0
∣
V
)
]
=
E
[
E
(
Y
∣
X
=
1
,
V
)
−
E
(
Y
∣
X
=
0
,
V
)
]
E(Y_1)-E(Y_0)=E[E(Y_1-Y_0|V)]=E[E(Y|X=1,V)-E(Y|X=0,V)]
E(Y1)−E(Y0)=E[E(Y1−Y0∣V)]=E[E(Y∣X=1,V)−E(Y∣X=0,V)]
可忽略性假定解释了随机化试验和观察性研究的差别. 如果处理
X
X
X 没有随机分配, 而仅仅是可忽略性假定成立, 那么不对混杂因素进行调整, 就会导致混杂偏倚,

当协变量 V 的分布在处理组和对照组不均衡时, 该混杂偏倚一
般不为零, 因此在进行平均因果作用的统计推断时, 需要对协变量 V 做调整.
在可忽略性假定下, 多种统计推断方法可以用来估计因果作用. 例如,当
V
V
V 是一个有
K
K
K 个水平
的离散变量时, 可以先在 V 的每一层估计
A
C
E
k
=
E
(
Y
1
−
Y
0
∣
V
=
k
)
ACE_k=E(Y_1-Y_0|V=k)
ACEk=E(Y1−Y0∣V=k)然后估计:
A
C
E
=
∑
k
=
1
K
A
C
E
k
p
r
(
V
=
k
)
ACE= \sum^K_{k=1} ACE_kpr(V=k)
ACE=k=1∑KACEkpr(V=k)
但是, 当 V 是高维变量或连续型变量时, 按
V
V
V 的值将总体分层会导致每一层的样本太少, 增大估计的方差. 在这种情形下, 通常建立一些参数模型来估计因果作用.
倾向得分和匹配
为了消除协变量的分布在处理组与对照组之间的差异, 匹配 (matching) 方法经常用在观察性研究中. 匹配方法的目的是对每一个个体匹配一个具有相同或相近协变量取值的个体集合, 使得匹配得到的数据在处理组和对照组有相同的协变量分布, 然后根据匹配数据推断因果作用. 早期的匹配方法根据一个或几个协变量直接构造匹配集合,协变量维数较高, 难以决定根据哪些协变量构造匹配集合
这是会用倾向性匹配得分(Propensity score matching)根据一个
一维的倾向得分构造匹配集合, 目前已经是观察性研究中常使用的匹配方法.
定义:
倾向得分定义为条件概率 π ( V ) = p r ( X = 1 ∣ V ) \pi(V)=pr(X=1|V) π(V)=pr(X=1∣V)
定理:
如果给定协变量
V
V
V 时可忽略性成立,即
Y
X
∐
X
∣
V
且
0
<
p
r
(
X
=
1
∣
V
)
<
1
Y_X \coprod X|V 且0<pr(X=1|V)<1
YX∐X∣V且0<pr(X=1∣V)<1
那么,给定倾向得分
π
(
V
)
\pi(V)
π(V)时可忽略性也成立,即
Y
X
∐
X
∣
π
(
V
)
且
0
<
p
r
{
X
=
1
∣
π
(
V
)
}
<
1
Y_X \coprod X| \pi(V) 且0<pr \{X=1| \pi(V)\} <1
YX∐X∣π(V)且0<pr{X=1∣π(V)}<1
因此, 可以利用倾向得分分层或匹配进行因果推断, 从而避免了用高维协变量
V
V
V 进行分层或匹配的困难. 给定样本中个体
i
=
1
,
.
.
.
,
n
i = 1, . . . , n
i=1,...,n,
个体
i
i
i根据倾向得分得到的匹配集合定义为:

其中
δ
{
⋅
}
\delta\{·\}
δ{⋅}是示性函数,当括号满足条件时,取值1,否则是0,M是整数,代表某一个个体的匹配数据个数.
平均因果作用匹配估计为:

如果在实际中不知道真实的倾向得分, 可以根据数据预先估计, 然后用估计得到的倾向得分做匹配. 常用的估计倾向得分方法包括 logistic 回归和决策树等机器学习方法
匹配方法还可以用来估计处理组的平均因果作用

在一定正则条件下, 可以证明匹配估计的相合性和渐近正态性.
在一定条件下, 使用倾向得分估计值进行匹配得到的平均因果作用估计的方差比使用倾向得分的真实值还小.
逆概加权估计和回归估计
除了匹配, 倾向得分还经常用在逆概加权估计 (inverse probability weighted estimation) 中. 给定可忽略性假定, 容易证明,

据此, 可以通过拟合一个倾向得分模型
π
(
V
;
α
)
=
p
r
(
X
=
1
∣
V
;
α
)
π(V ; α) = pr(X = 1 | V ; α)
π(V;α)=pr(X=1∣V;α)来估计平均因果作用. 倾向得分模型满足相应的矩方程
E
{
X
−
π
(
X
;
α
)
∣
V
}
=
0
E\{X − π(X; α) | V \} = 0
E{X−π(X;α)∣V}=0, 因此可以用经典的方法, 如广义矩估计 (generalized method of moments, GMM) 来估计未知参数
α
α
α. 得到参数估计
α
~
\tilde{\alpha}
α~ 后, 平均因果作用的逆概加权估计为

回归估计 (regression-based estimator) 需要建立一个对结果变量的回归模型,
E
(
Y
∣
X
,
V
)
=
m
(
X
,
V
;
γ
)
E(Y | X, V ) = m(X, V ; γ)
E(Y∣X,V)=m(X,V;γ). 为了估计平均因果作用, 需要先估计该模型的参数. 注意到该回归模型满足矩方程
E
{
Y
−
m
(
X
,
V
;
γ
)
∣
X
,
V
}
=
0
E\{Y − m(X, V ; γ) | X, V \} = 0
E{Y−m(X,V;γ)∣X,V}=0, 可以用经典的估计矩方程的方法来估计未知参数
γ
γ
γ. 在得到参数估计
γ
~
\tilde{γ}
γ~后, 平均因果作用的回归估计为
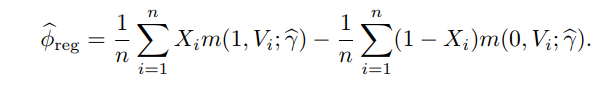
双稳健估计
将回归估计和逆概加权估计结合起来,并具有双稳健性质: 只要回归模型和倾向得分模型中的一个模型正确, 那么双稳健估计就有相合性.
双稳健估计同时需要一个回归模型
m
(
X
,
V
;
γ
)
=
E
(
Y
∣
X
,
V
;
γ
)
m(X, V ; γ) = E(Y | X, V ; γ)
m(X,V;γ)=E(Y∣X,V;γ) 和一个倾向得分模型
π
(
V
;
α
)
=
p
r
(
X
=
1
∣
V
;
α
)
π(V ; α) = pr(X = 1 | V ; α)
π(V;α)=pr(X=1∣V;α). 估计未知参数 (α, γ) 的方法如第 3.4 小节所述. 得到参数估计
(
α
~
,
γ
~
)
(\tilde{\alpha},\tilde{γ})
(α~,γ~) 后, 平均因果作用的双稳健估计为

上式的第一行等于逆概加权估计, 第二行是对逆概加权估计的一个纠偏项, 由逆概的残差和回归估计构成. 如果倾向得分模型正确, 那么逆概加权估计有相合性, 并且当样本量增加时第二行中的纠偏项趋于零. 这是因为, 根据大数定律, 上式中的第三项收敛到
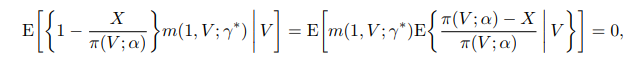
其中
γ
∗
=
p
l
i
m
γ
~
γ^∗ = plim \tilde{γ}
γ∗=plimγ~, 表示当样本量趋于无穷时
γ
~
\tilde{γ}
γ~ 依概率收敛的极限值. 同理第四项也收敛到 0. 因此,
ϕ
d
r
~
\tilde{ϕ_{dr}}
ϕdr~ 在倾向得分模型
π
(
V
;
α
)
π(V ; α)
π(V;α) 正确时有相合性. 注意, 当回归模型
m
(
X
,
V
;
γ
)
m(X, V ; γ)
m(X,V;γ) 错误时, 上面的推导仍然成立.
等价于:

第一行是回归估计, 第二行是对回归估计的一个纠偏项. 如果回归模型正确, 那么回归估计
有相合性, 而且可以证明, 无论倾向得分模型正确与否,当样本量增加时 第二行中的纠偏项趋于零, 因此, 在回归模型正确时有相合性, 而不需要倾向得分模型正确.
综上,
ϕ
d
r
~
\tilde{ϕ_{dr}}
ϕdr~ 具有双稳健性质. 相比于回归估计和倾向得分估计, 双稳健估计提供了更多减少估计偏
差的机会. 由于双稳健估计能有效地减小模型错误导致的偏差, 这种方法越来越广泛应用在缺失数据
分析和因果推断中.
但是要注意到, 当两个模型都不正确时,双稳健估计可能会比回归估计和逆概加权估计的偏差更大,当出现特别大或者特别小的倾向得分时, 偏差会被放大, 甚至出现不合理的估计结果. 例如, 对一个取 0 和 1 值的结果变量, 当两个模型都错误时, 双稳健估计可能会得到大于 1 的结果

























 700
700

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










