用于语义分割的Hausdorff损失函数

求则得之，舍则失之

已于 2022-07-22 15:41:06 修改

阅读量3k

点赞数 5

分类专栏： PyTorch 损失函数分割文章标签：人工智能 python

于 2022-07-16 20:00:00 首次发布

本文链接：https://blog.csdn.net/weixin_43229348/article/details/125818745

版权

PyTorch 同时被 3 个专栏收录

45 篇文章 56 订阅

订阅专栏

分割

7 篇文章 1 订阅

订阅专栏

损失函数

2 篇文章 0 订阅

订阅专栏

1.概述

当谈到距离时，我们通常指的是最短距离，例如，如果一个点X与多边形P的距离是D，我们通常假设D是X到P最近点的距离。同样的逻辑适用于多边形与多边形之间：如果两个多边形A和B彼此之间有一定的距离，我们通常理解的距离是A的任何一点和B的任何一点之间的最短距离。形式上，这被称为最小函数，因为A和B之间的距离D由下式表示:
$D(A,B)=min_{a\in A}\{{min_{b\in B}\{d(a,b)}\}\}$
这个方程读起来像一个计算机程序:对于A中的每一点a，求出它到B中的任何一点b的最小距离；最后，求得所有a点中最小值。

在某些应用中，多边形之间距离的定义可能变得相当不令人满意；让我们看看图1。我们可以说三角形之间的距离很近，考虑到它们的最短距离，由它们的红色顶点表示。然而，我们自然会认为这些多边形之间的小距离意味着一个多边形的任何一点都不会远离另一个多边形。从这个意义上说，图1所示的两个多边形不是很近，因为它们最远的点(蓝色部分)实际上可能离另一个多边形很远。很明显，最短距离完全独立于每个多边形形状。

$图 1 ：没有考虑形状的最短距离$

另一个例子如图2给出的，我们有相同的两个三角形，它们的最短距离与图1相同，但位置不同。很明显，最短距离的概念所包含的信息量非常低，因为距离的值与之前的情况没有变化，而物体却发生了变化。

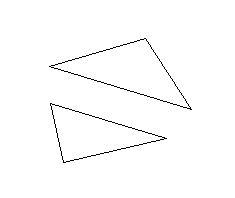
$图 2 ：最短距离并不能说明物体的位置$

正如我们将在下一节中看到的，尽管Hausdorff距离看起来很复杂，但它确实捕捉到了被最短距离忽略了的这些细微之处。

2.Hausdorff距离

以菲利克斯·豪斯多夫(Felix Hausdorff, 1868-1942)命名，Hausdorff距离是一个集合到另一个集合中最近点的最大距离。更正式地说，集合A到集合B的Hausdorff距离是一个极大值函数，定义为
$h(A,B)=max_{a\in A}\{{min_{b\in B}\{d(a,b)}\}\}$

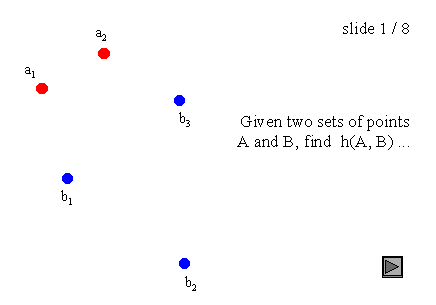
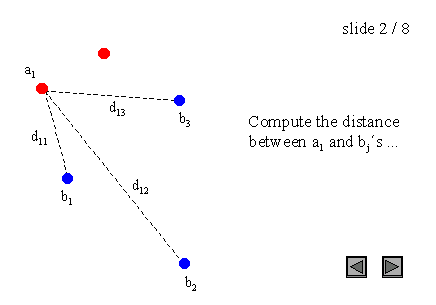
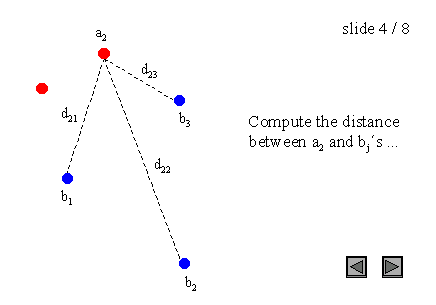
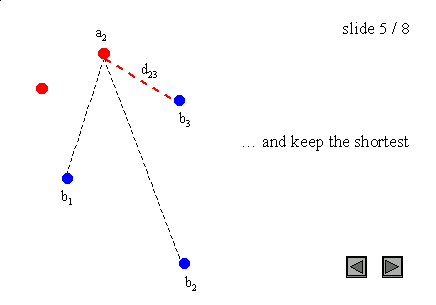
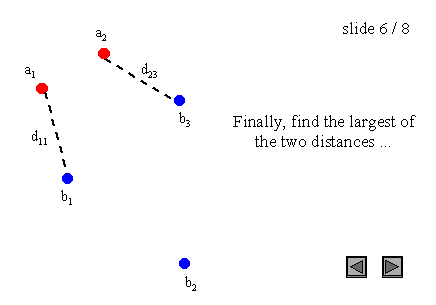
其中a和b分别是集合A和B的点，d(a, b)是这些点之间的任意度量;为了简单起见，我们将d(a, b)作为a和b之间的欧氏距离。例如，A和B是两组点，一个暴力算法将是：

1.  h = 0
2.  for every point ai of A,
      2.1  shortest = Inf ;
      2.2  for every point bj of B
                    dij = d (ai , bj )
                    if dij < shortest then
                              shortest = dij
      2.3  if shortest > h then
                    h = shortest

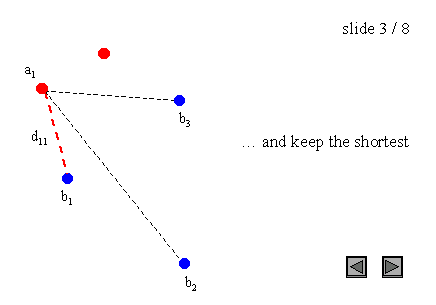
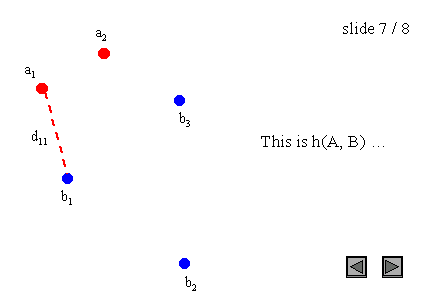
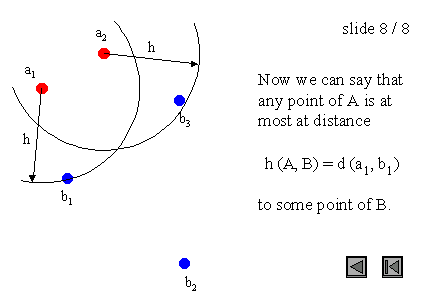
请添加图片描述

$图 3 : 点集上的 H a u s d or ff 距离$
显然，当每个集合的点数分别为n和m时候，该算法的运行时间为O(n m)。

需要注意的是，Hausdorff距离是有方向的(我们也可以说是不对称的)，这意味着大多数情况下h(A, B)不等于h(B, A)。这个一般条件也适用于图3的例子，因为h(A, B) = d(a1, b1)，而h(B, A) = d(b2, a1)。这种不对称性是极大极小函数的一个性质，而极小极小函数是对称的。

Hausdorff距离的更一般的定义是： $H (A, B) = max \{ h (A, B), h (B, A) \}$
其中定义了A和B之间的Hausdorff距离。两个距离h(A, B)和h(B, A)有时被称为A到B前向和后向Hausdorff距离。除非另有说明，从现在起，我们在说Hausdorff距离时指的就是上面更一般的定义。

还记得图1中的多边形吗?他们的一些观点很接近，但不是所有的。豪斯多夫距离(Hausdorff distance)通过表示一个多边形的任意点到另一个多边形之间的最大距离，给出了一个有趣的测量它们相互接近程度的方法。比最短距离法更好，它只适用于每个多边形的一个点，而不考虑多边形的所有其他点。
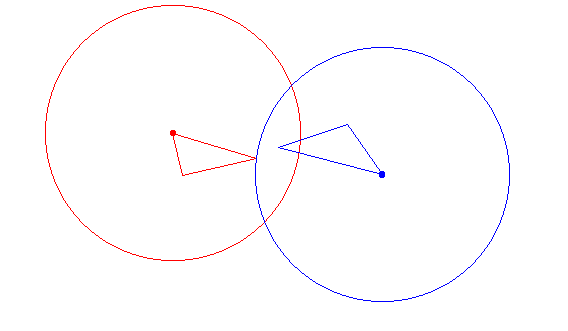
请添加图片描述
$图 4 ：图 1 中每个三角形的极值周围所示的豪斯多夫距离。每个圆的半径是 H (P 1, P 2)$

另一个问题是最短距离对多边形位置不敏感。我们看到这个距离完全没有考虑到多边形的分布。这里，Hausdorff距离再次具有对位置敏感的优势，如图5所示。
请添加图片描述
$图 5 ：图 4 中三角形在最短距离相同但位置不同时的 H a u s d or ff 距离。$

3.计算凸多边形之间的Hausdorff距离

3.1 假设条件

在接下来的讨论中，我们假设关于多边形A和B有以下事实:

1).多边形A和多边形B是简单凸多边形;
2).多边形A和多边形B互不相交,也就是说:
- 它们不相交;
- 没有一个多边形包含另一个多边形。

下一节解释的算法是基于这里给出的三个几何观测。为了简化文本，我们假设两个点a和b分别属于多边形AA和B，这样:
$d (a, b) = h (A, B)$
简单来说，a是多边形A相对于多边形B的最远点，而b是多边形B相对于多边形A的最近点。

引理1:
ab在a点的垂线是A的支撑线，相对于这条线，A和B在同一边。
引理1 b:
ab在b点的垂线是B的支撑线，a和B相对于这条线在不同的两边。
引理2:
A的一个顶点x使得x到B的距离等于h (A, B)
引理3:
设 $b_i$ 是B中距离顶点 $a_i$ 最近的点。如果µ是 $b_i$ 到 $b_{i+1}$ 的移动方向(顺时针或逆时针)，那么在A的所有顶点的一个完整循环中，µ的变化不超过两次。

3.3 算法

本文提出的算法是由 [Atallah83] 提出的。它的基本策略是依次计算h(A,B)和h(B, A)；由于引理2，不需要查询起始多边形的每个点，只需要查询它的顶点。

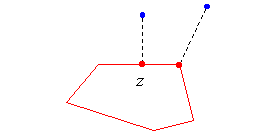
该算法使用的一个重要事实是，最近点只能是目标多边形的顶点，或者垂直于其边之一垂足z。
这一事实提出了一个函数来检查是否存在可能的最近点。给定一个源点a和一个由点b1和顶点b2定义的目标边缘：
请添加图片描述

Function z = CheckForClosePoint (a, b1 , b2 ) :
Compute the position z where the line that passes through b1 and b2 crosses its perpendicular through a  ;
if z is between b1 b2 then return z ;
else compute at b2 a line P perpendicular to the line ab2 ;
        if P is a supporting line of B then return b2 ;
        else return NULL.

该函数显然使用引理1b来确定B的最近点是否位于目标边缘，应该是靠近a的。根据引理3，它还假设源点a和b2不在b1点与**[b1b2]**的垂线的不同边。

现在我们准备好了主算法;假设两个多边形的顶点都是逆时针枚举的:

Algorithm for computing h(A, B) :
1.  From a1, find the closest point b1 and compute d1 = d ( a1, b1 )
2.  h(A, B) = d1
3.  for each vertex ai of A,
      3.1  if $a_{i+1}$ is to the left of aibi
                     find $b_{i+1}$ , scanning B counterclockwise with CheckForClosePoint from bi
              if $a_{i+1}$ is to the right of aibi
                     find $b_{i+1}$ , scanning B clockwise with CheckForClosePoint from bi
              if $a_{i+1}$ is anywhere on aibi
                      $b_{i+1}$ = bi
      3.2  Compute $d_{i+1}$ = d ($a_{i+1}$ , $b_{i+1}$ )
      3.3  h (A, B) = max { h (A, B), $d_{i+1}$ }

3.4 复杂度

如果多边形A和B分别有n和m个顶点，则:

步骤1：显然可以在O(m)时间内完成;
步骤2：时间为常数O(1);
步骤3：将执行(n-1)次，即O(n);
步骤3.1：执行的总次数不会超过O(2m)。这是引理3的一个结果，它保证多边形B不能被扫描超过两次;
步骤3.2和3.3：完成时间为常数O(1)

因此计算h(A, B)的复杂度为： $O (m) + O (n) + O (2 m) = O (n + m)$
为了找到H(A, B)，算法需要执行两次；计算Hausdorff距离的总复杂度与 O(n+m) 保持线性关系。

4.PyTorch代码实现

import torch
import torch.nn as nn
import cv2 as cv
import numpy as np
# from scipy.ndimage.morphology import distance_transform_edt as edt
from scipy.ndimage import distance_transform_edt as edt
from scipy.ndimage import convolve


def torch2D_Hausdorff_distance(x, y):  # Input be like (Batch,width,height)
    x = x.float()
    y = y.float()
    distance_matrix = torch.cdist(x, y, p=2)  # p=2 means Euclidean Distance

    value1 = distance_matrix.min(2)[0].max(1, keepdim=True)[0]
    value2 = distance_matrix.min(1)[0].max(1, keepdim=True)[0]

    value = torch.cat((value1, value2), dim=1)

    return value.max(1)[0].mean()


class HausdorffLoss(nn.Module):
    def __init__(self, p=2):
        super(HausdorffLoss, self).__init__()
        self.p = p

    def torch2D_Hausdorff_distance(self, x, y, p=2):  # Input be like (Batch,1, width,height) or (Batch, width,height)
        x = x.float()
        y = y.float()
        distance_matrix = torch.cdist(x, y, p=p)  # p=2 means Euclidean Distance

        value1 = distance_matrix.min(2)[0].max(1, keepdim=True)[0]
        value2 = distance_matrix.min(1)[0].max(1, keepdim=True)[0]

        value = torch.cat((value1, value2), dim=1)

        return value.max(1)[0].mean()

    def forward(self, x, y):  # Input be like (Batch,height,width)
        loss = self.torch2D_Hausdorff_distance(x, y, self.p)
        return loss


class HausdorffDTLoss(nn.Module):
    """Binary Hausdorff loss based on distance transform"""

    def __init__(self, alpha=2.0, **kwargs):
        super(HausdorffDTLoss, self).__init__()
        self.alpha = alpha

    @torch.no_grad()
    def distance_field(self, img: np.ndarray) -> np.ndarray:
        field = np.zeros_like(img)

        for batch in range(len(img)):
            fg_mask = img[batch] > 0.5

            if fg_mask.any():
                bg_mask = ~fg_mask

                fg_dist = edt(fg_mask)
                bg_dist = edt(bg_mask)

                field[batch] = fg_dist + bg_dist

        return field

    def forward(
            self, pred: torch.Tensor, target: torch.Tensor, debug=False
    ) -> torch.Tensor:
        """
        Uses one binary channel: 1 - fg, 0 - bg
        pred: (b, 1, x, y, z) or (b, 1, x, y)
        target: (b, 1, x, y, z) or (b, 1, x, y)
        """
        assert pred.dim() == 4 or pred.dim() == 5, "Only 2D and 3D supported"
        assert (
                pred.dim() == target.dim()
        ), "Prediction and target need to be of same dimension"

        # pred = torch.sigmoid(pred)

        pred_dt = torch.from_numpy(self.distance_field(pred.detach().cpu().numpy())).float()
        target_dt = torch.from_numpy(self.distance_field(target.detach().cpu().numpy())).float()

        pred_error = (pred - target) ** 2
        distance = pred_dt ** self.alpha + target_dt ** self.alpha

        dt_field = pred_error * distance
        loss = dt_field.mean()

        if debug:
            return (
                loss.cpu().numpy(),
                (
                    dt_field.cpu().numpy()[0, 0],
                    pred_error.cpu().numpy()[0, 0],
                    distance.cpu().numpy()[0, 0],
                    pred_dt.cpu().numpy()[0, 0],
                    target_dt.cpu().numpy()[0, 0],
                ),
            )

        else:
            return loss


class HausdorffERLoss(nn.Module):
    """Binary Hausdorff loss based on morphological erosion"""

    def __init__(self, alpha=2.0, erosions=10, **kwargs):
        super(HausdorffERLoss, self).__init__()
        self.alpha = alpha
        self.erosions = erosions
        self.prepare_kernels()

    def prepare_kernels(self):
        cross = np.array([cv.getStructuringElement(cv.MORPH_CROSS, (3, 3))])
        bound = np.array([[[0, 0, 0], [0, 1, 0], [0, 0, 0]]])

        self.kernel2D = cross * 0.2
        self.kernel3D = np.array([bound, cross, bound]) * (1 / 7)

    @torch.no_grad()
    def perform_erosion(
            self, pred: np.ndarray, target: np.ndarray, debug
    ) -> np.ndarray:
        bound = (pred - target) ** 2

        if bound.ndim == 5:
            kernel = self.kernel3D
        elif bound.ndim == 4:
            kernel = self.kernel2D
        else:
            raise ValueError(f"Dimension {bound.ndim} is nor supported.")

        eroted = np.zeros_like(bound)
        erosions = []

        for batch in range(len(bound)):

            # debug
            erosions.append(np.copy(bound[batch][0]))

            for k in range(self.erosions):

                # compute convolution with kernel
                dilation = convolve(bound[batch], kernel, mode="constant", cval=0.0)

                # apply soft thresholding at 0.5 and normalize
                erosion = dilation - 0.5
                erosion[erosion < 0] = 0

                if erosion.ptp() != 0:
                    erosion = (erosion - erosion.min()) / erosion.ptp()

                # save erosion and add to loss
                bound[batch] = erosion
                eroted[batch] += erosion * (k + 1) ** self.alpha

                if debug:
                    erosions.append(np.copy(erosion[0]))

        # image visualization in debug mode
        if debug:
            return eroted, erosions
        else:
            return eroted

    def forward(
            self, pred: torch.Tensor, target: torch.Tensor, debug=False
    ) -> torch.Tensor:
        """
        Uses one binary channel: 1 - fg, 0 - bg
        pred: (b, 1, x, y, z) or (b, 1, x, y)
        target: (b, 1, x, y, z) or (b, 1, x, y)
        """
        assert pred.dim() == 4 or pred.dim() == 5, "Only 2D and 3D supported"
        assert (
                pred.dim() == target.dim()
        ), "Prediction and target need to be of same dimension"

        # pred = torch.sigmoid(pred)

        if debug:
            eroted, erosions = self.perform_erosion(
                pred.detach().cpu().numpy(), target.detach().cpu().numpy(), debug
            )
            return eroted.mean(), erosions

        else:
            eroted = torch.from_numpy(
                self.perform_erosion(pred.cpu().numpy(), target.cpu().numpy(), debug)
            ).float()

            loss = eroted.mean()

            return loss


if __name__ == "__main__":
    u = torch.Tensor([[[1.0, 0.0],
                       [0.0, 1.0],
                       [-1.0, 0.0],
                       [0.0, -1.0]],
                      [[1.0, 0.0],
                       [0.0, 1.0],
                       [-1.0, 0.0],
                       [0.0, -1.0]],
                      [[2.0, 0.0],
                       [0.0, 2.0],
                       [-2.0, 0.0],
                       [0.0, -4.0]]])

    v = torch.Tensor([[[0.0, 0.0],
                       [0.0, 2.0],
                       [-2.0, 0.0],
                       [0.0, -3.0]],
                      [[2.0, 0.0],
                       [0.0, 2.0],
                       [-2.0, 0.0],
                       [0.0, -4.0]],
                      [[1.0, 0.0],
                       [0.0, 1.0],
                       [-1.0, 0.0],
                       [0.0, -1.0]]])

        print("Input shape is (B,W,H):", u.shape, v.shape)
    HD = HausdorffLoss()
    HD1 = HausdorffDTLoss()
    HD2 = HausdorffERLoss()
    hdLoss = HD(u, v)
    hdLoss1 = HD1(u.reshape(u.shape[0], 1, *u.shape[1:]), v.reshape(v.shape[0], 1, *v.shape[1:]))
    hdLoss2 = HD2(u.reshape(u.shape[0], 1, *u.shape[1:]), v.reshape(v.shape[0], 1, *v.shape[1:]))
    # hdLoss = torch2D_Hausdorff_distance(u, v)

    print("Hausdorff Distance is:", hdLoss)
    print("Hausdorff Distance is:", hdLoss1)
    print("Hausdorff Distance is:", hdLoss2)
    # Input shape is (B,W,H): torch.Size([3, 4, 2]) torch.Size([3, 4, 2])
	# Hausdorff Distance is: tensor(2.6667)
	# Hausdorff Distance is: tensor(8.3750)
	# Hausdorff Distance is: tensor(0.6541)

BONUS

python简单实现Hausdorff

"""Get the Hausdorff Distance between the two contours"""
def getHDDistance(contour1, contour2):
	#d1 = hd.computeDistance(contour1, contour2)
	#return d1

	#For each point in c1
		#Find the closest point in c2
		#If this is larger than the current largest min
			#Set the largest min to this
	largestMin = -1
	for point1 in contour1:
		minDist = -1
		for point2 in contour2:
			dist = math.sqrt(pow((point1[0][0] - point2[0][0]), 2) + pow((point1[0][1] - point2[0][1]), 2))
			if minDist == -1 or dist < minDist:
				minDist = dist
		if minDist > largestMin:
			largestMin = minDist
	return largestMin

OpenCV实现的Hausdorff简单实用

def test_computeDistance():
        a = cv.imread(os.path.join(MODULE_DIR, 'samples/data/shape_sample/1.png'), cv.IMREAD_GRAYSCALE)
        b = cv.imread(os.path.join(MODULE_DIR, 'samples/data/shape_sample/2.png'), cv.IMREAD_GRAYSCALE)
      
        ca, _ = cv.findContours(a, cv.RETR_CCOMP, cv.CHAIN_APPROX_TC89_KCOS)
        cb, _ = cv.findContours(b, cv.RETR_CCOMP, cv.CHAIN_APPROX_TC89_KCOS)

        hd = cv.createHausdorffDistanceExtractor()
        sd = cv.createShapeContextDistanceExtractor()
		
		d1 = hd.computeDistance(ca[0], cb[0])
        d2 = sd.computeDistance(ca[0], cb[0])

参考目录

https://github.com/JunMa11/SegLoss/blob/master/losses_pytorch/hausdorff.py
https://medium.com/@junma11/loss-functions-for-medical-image-segmentation-a-taxonomy-cefa5292eec0

求则得之，舍则失之

关注

5
点赞
踩
21

收藏

觉得还不错? 一键收藏
2
评论
用于语义分割的Hausdorff损失函数

当谈到距离时，我们通常指的是最短距离，例如，如果一个点与多边形的距离是，我们通常假设是到最近点的距离。同样的逻辑适用于多边形与多边形之间如果两个多边形和彼此之间有一定的距离，我们通常理解的距离是的任何一点和的任何一点之间的。形式上，这被称为最小函数，因为和之间的距离D(A,B)=mina∈A{minb∈B{d(a,b)}}这个方程读起来像一个计算机程序对于中的每一点，求出它到中的任何一点的最小距离；最后，求得所有点中最小值。。图1图。......
复制链接

扫一扫