【Simulink】三相两电平四桥臂离网型逆变器(4L 2LVSI)连续控制集模型预测控制(CCS-MPC)

之前写过一篇【Simulink】三相两电平四桥臂离网型逆变器(4L 2LVSI)有限控制集模型预测控制(FCS-MPC)，这篇博客把控制方法从有限控制集模型预测控制(FCS-MPC)改成连续控制集模型预测控制(CCS-MPC)。CCS-MPC比FCS-MPC多了调制结构，开关频率固定。

1.四桥臂逆变器应用背景

传统的三桥臂逆变器不适合具有不平衡和非线性负载的应用，而三相四桥臂逆变器可以提供控制中性电流的路径，可以在各种负载条件下产生无失真的三相正弦输出。三相四桥臂逆变器可用于给三相不对称负载供电的变频器和航空机载变速恒频发电系统。

2.三相两电平四桥臂逆变器

four-leg two-level VSI(4L 2LVSI)连接形式类似于传统的三相逆变器，只是多了第四桥臂，连接到负载的中性点。

LC滤波

3.三相两电平四桥臂逆变器控制

参考：杨晨涛.三相四桥臂逆变器的预测控制策略研究[D].哈尔滨工业大学,2021.DOI:10.27061/d.cnki.ghgdu.2021.003567.

模型预测控制通常基于电路的状态空间方程，对逆变器电路的各相进行整体控制，无需考虑解耦问题，也不需要进行旋转变换。

定义电压电流矢量：

其中，$U_d$是逆变器输出电压（离散状态），$U$是逆变器输出电压（连续状态），$i$是逆变器输出电流，$U_o$是负载电压，$i_o$是负载电流。

根据基尔霍夫电流电压定律，可得：

$L\frac{di}{dt}=U-U_o$
$C\frac{d{U}_o}{dt}=i-i_o$

整理可得连续时间下的状态空间方程：

其中，

在实际应用中，预测模型是离散状态的，所以需要进行离散化。离散化方法主要可分为精确化和近似化两种方法。精确法利用状态方程的求解公式以保证在采样时刻，离散后的状态方程的解仍与原状态方程的解相同。近似法通常采用前向欧拉法，用状态变量的差商代替微商，进而求得离散化状态方程，在计算上相对简单，但通常适用于采样周期较小且对精度要求不高的场合。
☝️这些在现代控制理论课上有学到

这里采用精确化方法进行离散化：

在电压型四桥臂逆变器中，控制对象为负载电压。

区别于FCS-MPC，CCS-MPC中不直接得到开关器件的控制信号，而是先获得电压矢量$U(k)$。而后将其输出给调制级，由调制环节获得PWM信号，对于调制级来说$U(k)$即为参考电压矢量。$U(k)$不具有限定的数量，遍历的方式不可行，而是需要通过一定方式对其求解。

这样就得到了$U(k)$，不是通过遍历求解，而是将代价函数设为0，反向求解$U(k)$，接着将$U(k)$作为参考量输入至调制环节。调制方法采用和之前博客一样的方法：【Simulink】三相两电平四桥臂逆变器(4L 2LVSI)比例谐振(PR)控制

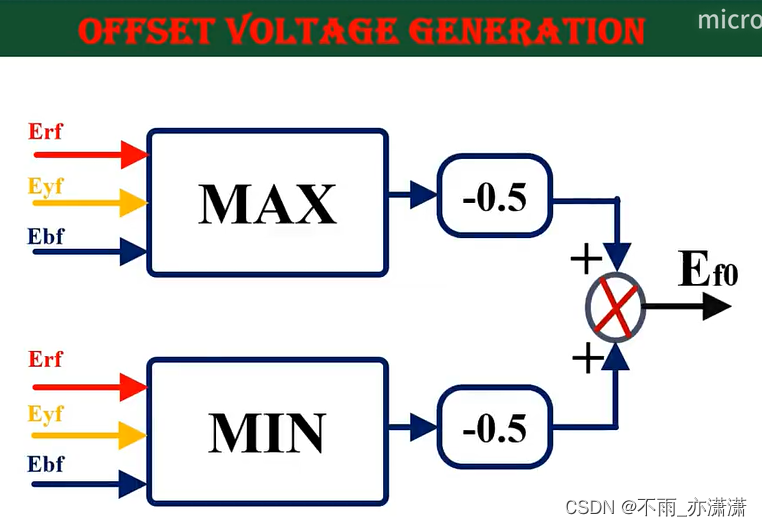
无需经过参考矢量区域判别及占空比计算等步骤，减少计算量。

4.Simulink仿真

4.1 仿真原理图

三相四桥臂

（这里其实有个小问题，建模的时候忽略了中性线电感Ln，但是仿真的时候出现了Ln，这个问题大家知道就好）

负载部分：

阻性负载为 12.1Ω 电阻，感性负载为 12.1Ω 电阻串联 0.1mH 电感，容性负载为 12.1Ω 电阻串联 10μF 电容。

4.2 仿真结果

4.2.1 三相平衡负载

负载电压：

FFT分析：

负载电流：

4.2.2 三相不平衡负载

负载电压：

FFT分析：

负载电流：

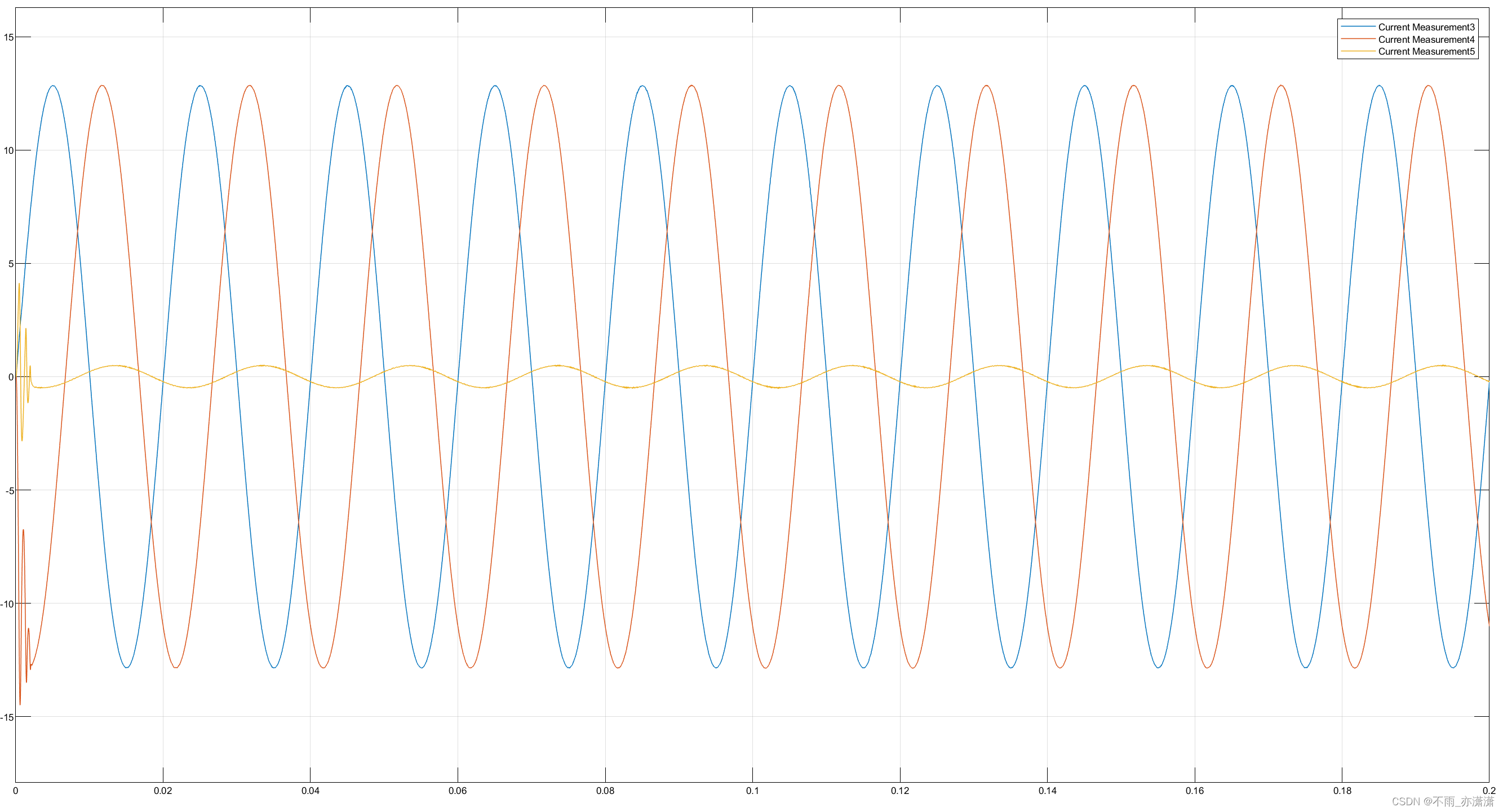
4.2.3 单相带载

负载电压：

FFT分析：

负载电流：

4.2.4 单相负载切换

负载电压：

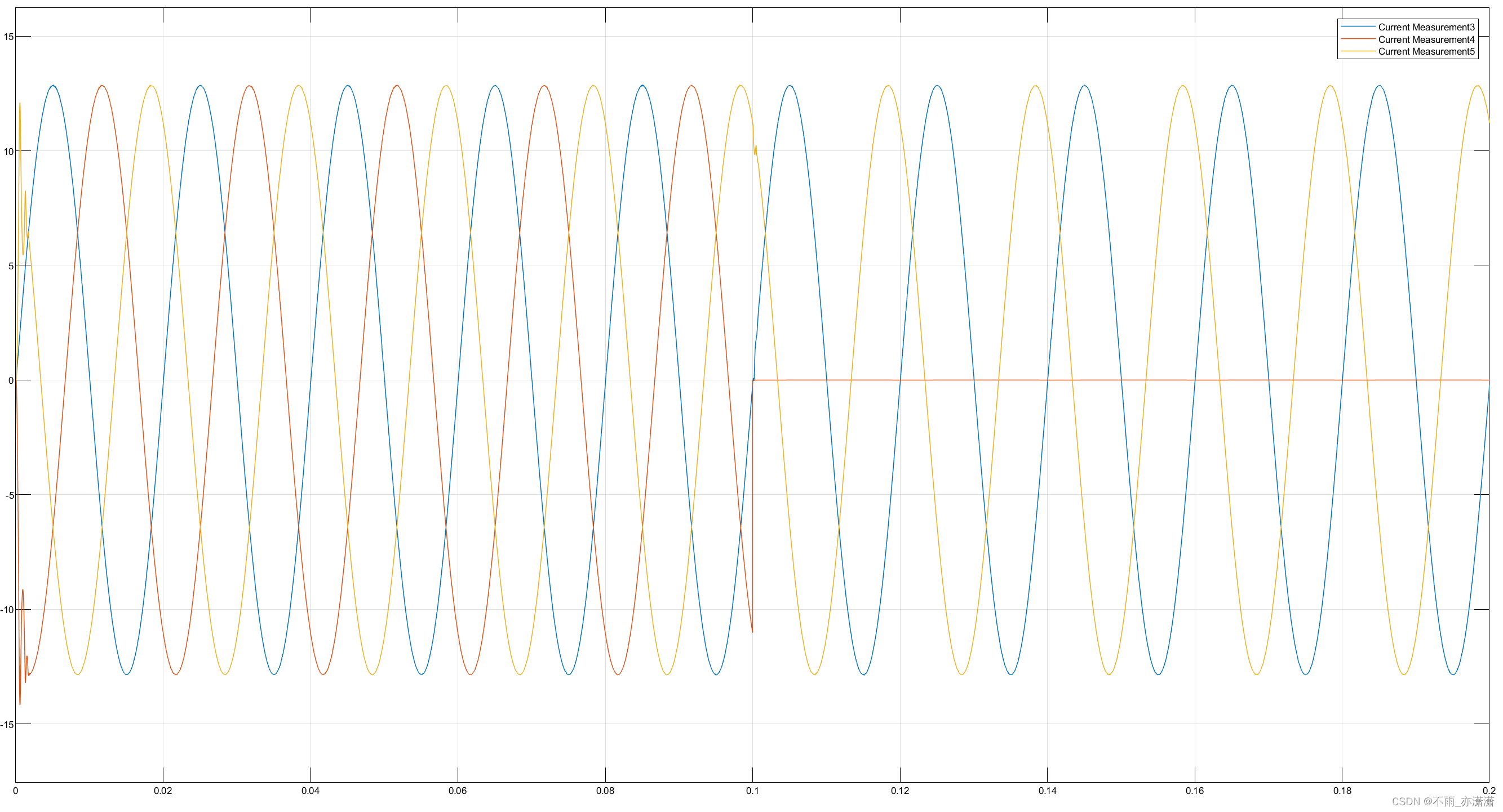
FFT分析：

负载电流：

结论：
在不同的负载状况下依然能够维持三相输出电压的平衡。
CCS-MPC方法在不同负载状况下的稳态误差和THD相比FCS-MPC显著减小，但在暂态性能上有所降低

5.资源下载

传送门

参考

[1] 杨晨涛.三相四桥臂逆变器的预测控制策略研究[D].哈尔滨工业大学,2021.DOI:10.27061/d.cnki.ghgdu.2021.003567.
[2] Yaramasu, V., et al. “Cost-function based predictive voltage control of two-level four-leg inverters using two step prediction horizon for standalone power systems.” 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC). IEEE, 2012. （推导结果似乎有一点点问题）