在画控制系统方框图时，需要将从输入量到输出量的所有中间变量及传递函数写出，以便画图，在电路系统中时常遇到电感和电容，其传递函数和s域电路模型推导如下：
1.电容传递函数：
电容输入输出关系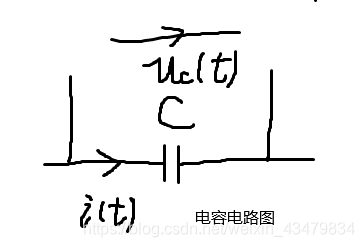
以
u
c
(
t
)
u_c(t)
uc(t)为输出，
i
(
t
)
i(t)
i(t)为输入，则有：
i
(
t
)
=
C
d
u
c
(
t
)
d
t
i(t)=C \frac{du_c(t)}{dt}
i(t)=Cdtduc(t)
对两边同时进行拉氏变换时：
I
(
s
)
=
C
(
s
U
c
(
s
)
−
u
c
(
0
)
)
I(s)=C(sU_c(s)-u_{c}(0))
I(s)=C(sUc(s)−uc(0))
进行一下等效变换得到：
U
c
(
s
)
=
I
c
(
s
)
s
C
+
u
c
(
0
)
s
U_{c}(s)=\frac{I_{c}(s)}{sC}+\frac{u_{c}(0)}{s}
Uc(s)=sCIc(s)+suc(0)
其中
u
c
(
0
)
u_{c}(0)
uc(0)是电容在初始时刻的电压值，如果电感初始时刻有电压不能舍去，可以将其视作一个无初始电压的电感和一个电压源串联，如下图所示：
忽略初始电压或将其等效为电压源后，就可以得到电容两端的传递函数：
U
c
(
s
)
I
(
s
)
=
1
s
C
\frac{U_c(s)}{I(s)}=\frac{1}{sC}
I(s)Uc(s)=sC1
2.电感传递函数
以
i
L
(
t
)
i_L(t)
iL(t)作为输入，
u
L
(
t
)
u_L(t)
uL(t)作为输出，则有：
u
L
(
t
)
=
L
d
i
L
(
t
)
d
t
u_L(t)=L\frac{di_L(t)}{dt}
uL(t)=LdtdiL(t)
同样两边同时进行拉氏变换得到:
U
L
(
s
)
=
L
(
s
I
L
(
s
)
−
i
L
(
0
)
)
U_L(s)=L(sI_L(s)-i_{L}(0))
UL(s)=L(sIL(s)−iL(0))
等效电路模型为：
此时忽略电感初始电流或将其等效为电压源后电感两端
传递函数为：
U
L
(
s
)
I
L
(
s
)
=
s
L
\frac{U_L(s)}{I_L(s)}=sL
IL(s)UL(s)=sL
扫一扫
1112
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
