1 Introduction
凸优化在工程领域发挥着重要作用,这个系列根据standford EE364a 的convex optimization 课程,进行梳理总结。
2 优化问题
2.1 常见的优化问题
2.1.1 决策类的优化问题
设定目标,考虑限制,给出决策。

2.1.2 模型参数辨识
选定模型,带入数据,计算系数。
此时目标是降低模型的预测误差,参数必须在合理的区间,给出最小的参数。

2.2 数学抽象
构建工程的最优化问题,constraints一般比较容易构建,如何选定object 函数非常关键。

2.3 优化问题的解法
线性问题比较容易得到解答,对于优化问题同样。

具体的案例,控制每个光源的强度,使得镜面的光源强度和设定值的差值最小。

o点的光源强度为:
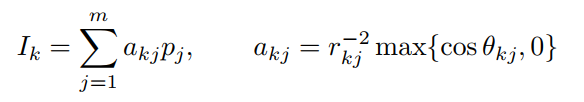
镜面的光源强度的最大误差为:
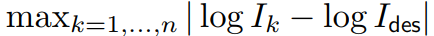
光源强度的物理限制为:
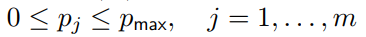
目标函数可以表示成
f
o
(
x
)
=
m
a
x
k
=
1
,
.
.
n
∣
I
k
−
I
d
e
s
∣
=
m
a
x
k
=
1
,
.
.
n
∣
∑
a
k
j
p
j
−
I
d
e
s
∣
\begin{aligned} f_o(x)= &max_{k=1,..n}|I_k-I_{des}| \\ =& max_{k=1,..n}|\sum a_{kj}p_j-I_{des}| \end{aligned}
fo(x)==maxk=1,..n∣Ik−Ides∣maxk=1,..n∣∑akjpj−Ides∣
形式和线性规划比较接近,但是具体如何转换,需要进一步学习。
3 convex set
3.1 convex optimization problem
如果可行的解集是一个convex set,解决这样的优化问题,一般比较简单。
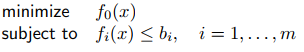
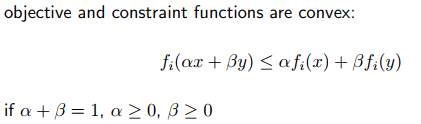
需要研究convex set的特性,帮助我们分辨问题是否是convex optimization问题,以及将问题转换成convex optimization的问题。
3.2 convex set的定义
在 进 入 各 种 集 合 定 义 之 前 , 一 定 要 记 住 , s e t 是 特 殊 的 一 类 向 量 组 成 。 \color{red}{在进入各种集合定义之前,一定要记住,set是特殊的一类向量组成。} 在进入各种集合定义之前,一定要记住,set是特殊的一类向量组成。
3.2.1 affine set
通过affine set 定义线段、射线和直线。

3.2.2 convex set
convex set的数学定义和几何直觉容易理解。
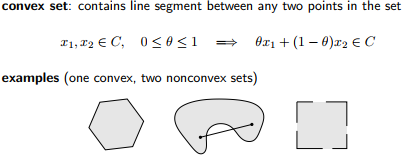
3.3 与convex set类似的集合
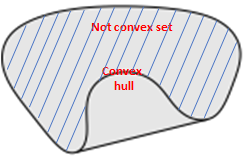
3.3.1 有限范围集合convex hull
有convex set必然就会有不是convex set的集合,将不是convex set的集合,转换成convex hull(convex hull 也是convex set)。
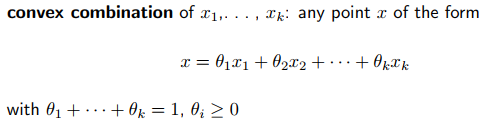
-
球集合

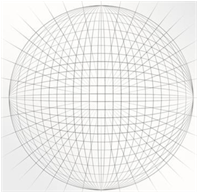
-
椭圆集合
从几何的角度,向量 x − x c x-x_c x−xc先转换到特征向量组成的向量空间中,然后在相应的特征向量方向,除以特征值,经过这样处理后的向量点积就是1。
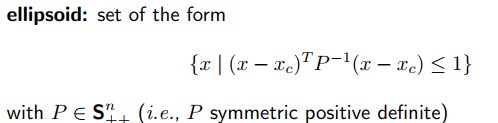
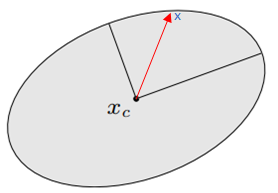
3.3.2 平面无限大集合
我 们 从 三 维 空 间 的 角 度 去 理 解 下 面 各 种 集 合 。 \color{red}{我们从三维空间的角度去理解下面各种集合。} 我们从三维空间的角度去理解下面各种集合。
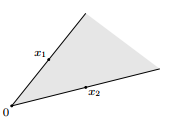
- convex cone
convex cone范围是无穷大的,构成一个扇形区域,同时也是convex set。
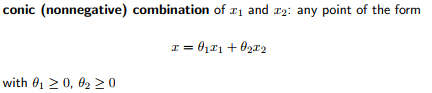
3.3.3 空间无限大集合
我 们 从 三 维 空 间 的 角 度 去 理 解 下 面 各 种 集 合 。 \color{red}{我们从三维空间的角度去理解下面各种集合。} 我们从三维空间的角度去理解下面各种集合。
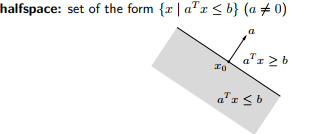
- half plane
a T x = b a^Tx=b aTx=b定义了一个平面,也是空间的分界面。
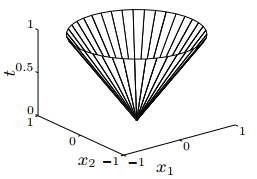
- norm cone
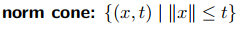
- Polyhedra
数学定义,几个平面相交构成的空间。
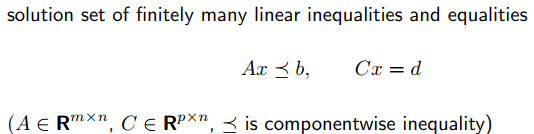
以下面这个图为例,
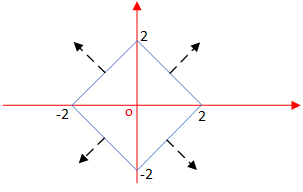
[ 1 1 − 1 1 − 1 − 1 1 − 1 ] [ x y ] ⪯ [ 2 2 2 2 ] \begin{bmatrix} 1 & 1 \\ -1 & 1 \\ -1 & -1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \preceq \begin{bmatrix} 2 \\ 2 \\ 2 \\ 2 \end{bmatrix} ⎣⎢⎢⎡1−1−1111−1−1⎦⎥⎥⎤[xy]⪯⎣⎢⎢⎡2222⎦⎥⎥⎤
需要注意的是,以集合中点(1, 1)为例,
A x = [ 2 ≤ 2 0 ≤ 2 − 2 ≤ 2 0 ≤ 2 ] ⪯ [ 2 2 2 28 ] Ax= \begin{bmatrix} 2 \leq 2 \\ 0 \leq 2 \\ -2 \leq 2 \\ 0 \leq 2 \end{bmatrix} \preceq \begin{bmatrix} 2 \\ 2 \\ 2 \\ 28 \end{bmatrix} Ax=⎣⎢⎢⎡2≤20≤2−2≤20≤2⎦⎥⎥⎤⪯⎣⎢⎢⎡22228⎦⎥⎥⎤
3.3.4 高维空间
- 半正定锥
s n = { X ∈ R n × n ∣ X = X T } s^n=\{X \in R^{n\times n} | X=X^T \} sn={X∈Rn×n∣X=XT}
例如
X = [ x y y z ] ∈ S + 2 X= \begin{bmatrix} x & y \\ y & z \end{bmatrix} \in S_+^2 X=[xyyz]∈S+2
是个维数为3的向量空间,其中满足 x ≥ 0 , z ≥ 0 , x z ≥ y 2 x \geq 0, z\geq 0, xz \geq y^2 x≥0,z≥0,xz≥y2,几何图像如下:

3.4 凸性不变的操作
3.4.1 交集
从集合的角度,凸集的交集是凸集,非常容易理解。
- example1
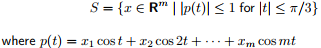
x是高维空间中的变量,p(t)并不容易用集合的方式画出图。为了从几何上理解更加方便,假定m=2,
p ( t ) = x 1 c o s ( t ) + x 2 c o s ( 2 t ) p(t)=x_1cos(t)+x_2cos(2t) p(t)=x1cos(t)+x2cos(2t)

发现(x1,x2)的集合并不能用集合的方式画出来,利用定义进行判断也非常的困难。
但是我们知道, t i ∈ [ − π 3 , π 3 ] t_i \in [-\frac{\pi}{3}, \frac{\pi}{3}] ti∈[−3π,3π]每个点都满足
− 1 ≤ [ c o s ( t i ) c o s ( 2 t i ) ] [ x 1 x 2 ] ≤ 1 -1\leq \begin{bmatrix} cos(t_i) & cos(2t_i) \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \leq1 −1≤[cos(ti)cos(2ti)][x1x2]≤1
这是一个典型的Polyhedra,所以是凸集。
( x 1 , x 2 ) (x_1,x_2) (x1,x2)的集合对所有的 t i t_i ti都满足上面的关系,所以
S = ∩ t i ∈ [ − π 3 , π 3 ] ∣ ∣ ( c o s ( t i ) , c o s ( 2 t i ) ) T x ∣ ∣ ≤ 1 S=\underset{t_i \in [-\frac{\pi}{3}, \frac{\pi}{3}]}{\cap} ||(cos(t_i), cos(2t_i))^Tx||\leq 1 S=ti∈[−3π,3π]∩∣∣(cos(ti),cos(2ti))Tx∣∣≤1
凸集的交集还是凸集,所以 ( x 1 , x 2 ) (x_1,x_2) (x1,x2)的集合是凸集。
3.4.2 仿射变换
仿射变换
f
(
x
⃗
)
=
A
x
⃗
+
b
⃗
f(\vec{x})=A{\vec{x}}+\vec{b}
f(x)=Ax+b
其中,
x
∈
R
n
,
A
∈
R
m
×
n
,
b
∈
R
m
x \in R^n, A \in R^{m\times n}, b\in R^m
x∈Rn,A∈Rm×n,b∈Rm。
因为仿射变换属于线性变换,并不会改变集合的凸性。
3.4.3 线性分式和透视函数
-
透视函数
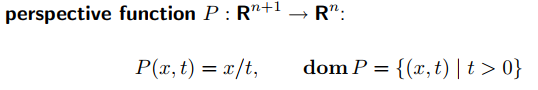
小孔成像问题中,
( R 3 中 的 ) (R^3中的) (R3中的)将实际位置点通过小孔投影在镜面上,镜面的图像时 R 2 R^2 R2。
镜面点的坐标 ( − x 1 x 3 , − x 2 x 3 ) (-\frac{x_1}{x_3}, -\frac{x_2}{x_3}) (−x3x1,−x3x2),这就是我们的透视函数。

通过透视,降维的操作时保凸的。 -
线性分式
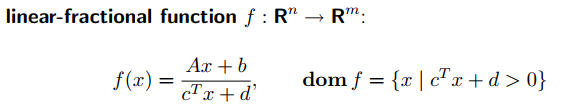
其中, A ∈ R n × m , b ∈ R m , c ∈ R n , d ∈ R A \in R^{n \times m}, b \in R^m, c \in R^n, d \in R A∈Rn×m,b∈Rm,c∈Rn,d∈R。
线性分式,可以看成是放射变换和透视变换的叠加,所以自然也是保凸的。
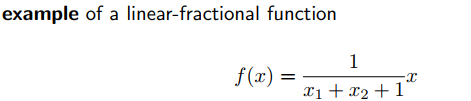
经过整理后,
f ( x ) = I x [ 1 , 1 ] T x + 1 f(x)=\frac{Ix}{[1, 1]^Tx+1} f(x)=[1,1]Tx+1Ix
4 广义不等式
4.1 正常锥
通过正常锥,推广出广义不等式。
下面三个条件的convex cone就是proper cone。

典型的几个proper cone:
1)非负象限,没有boundary,不知道为啥符合条件1;
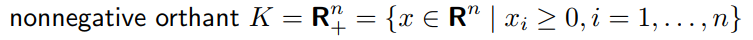
2)非负的多项式锥
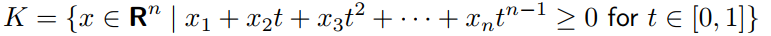
以二维多项式锥为例:
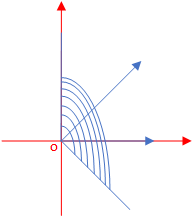
4.2 广义不等式定义及性质
4.2.1 广义不等式定义
通过正常锥,定义广义不等式。
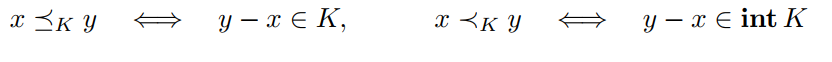
example1:
x、y必须是同一纬度的,但是分属不同的集合,每个纬度上满足
x
i
≤
y
i
x_i\leq y_i
xi≤yi
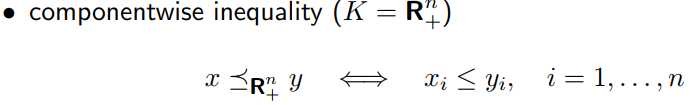
4.2.2 广义不等式性质
广义不等式的性质和普通不等式的性质类似
1)对于加法是保序的:
i
f
x
⪯
K
y
,
并
且
u
⪯
K
v
,
那
么
x
+
u
⪯
K
y
+
v
.
if x \preceq_K y, 并且u \preceq_K v, 那么x+u \preceq_K y+v.
ifx⪯Ky,并且u⪯Kv,那么x+u⪯Ky+v.
2)具有传递性:
i
f
x
⪯
K
y
,
并
且
y
⪯
K
z
,
那
么
x
⪯
K
z
.
if x \preceq_K y, 并且y \preceq_K z, 那么x \preceq_K z.
ifx⪯Ky,并且y⪯Kz,那么x⪯Kz.
3)对于非负数乘是保序的:
i
f
x
⪯
K
y
,
并
且
α
≥
0
,
那
么
α
x
⪯
K
α
y
.
if x \preceq_K y, 并且\alpha \geq 0, 那么\alpha x \preceq_K \alpha y.
ifx⪯Ky,并且α≥0,那么αx⪯Kαy.
4)自反的:
x
⪯
K
x
x \preceq_K x
x⪯Kx
5)反对称的:
i
f
x
⪯
K
y
,
并
且
y
⪯
K
x
,
那
么
x
⪯
K
y
.
if x \preceq_K y, 并且y \preceq_K x, 那么x \preceq_K y.
ifx⪯Ky,并且y⪯Kx,那么x⪯Ky.
4.2.3 最小与极小元
集合最小与极小元判断的时候则有很大的不同,先看定义。
对
于
每
个
y
∈
S
,
均
有
x
⪯
K
,
我
们
称
x
∈
S
(
关
于
广
义
不
等
式
⪯
K
)
的
最
小
元
,
它
是
唯
一
的
。
如
果
x
是
不
是
唯
一
的
,
则
称
x
∈
S
是
S
上
(
关
于
广
义
不
等
式
⪯
K
)
的
极
小
元
。
对于每个y \in S,均有x \preceq_K ,我们称x \in S(关于广义不等式 \preceq_K)的最小元,它是唯一的。\\ 如果x是不是唯一的,则称x \in S 是S上(关于广义不等式\preceq_K)的极小元。
对于每个y∈S,均有x⪯K,我们称x∈S(关于广义不等式⪯K)的最小元,它是唯一的。如果x是不是唯一的,则称x∈S是S上(关于广义不等式⪯K)的极小元。
example1:判断集合
S
1
S_1
S1中的极小元。
这是一个二维集合,如果如果
(
x
1
≤
x
i
,
y
1
≤
y
i
)
(x_1\leq x_i, y_1 \leq y_i)
(x1≤xi,y1≤yi)那么
x
1
x_1
x1是极小元。写成广义不等式的形式:
对
于
每
个
y
i
∈
S
1
,
均
有
x
⪯
K
y
,
其
中
K
=
R
+
n
对于每个y_i \in S_1, 均有x \preceq_K y, 其中K=R_+^n
对于每个yi∈S1,均有x⪯Ky,其中K=R+n
本题中,
a
⃗
∈
K
,
满
足
广
义
不
等
式
。
\vec{a} \in K,满足广义不等式。
a∈K,满足广义不等式。

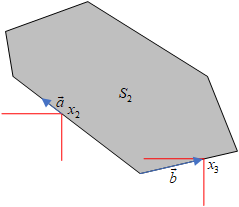
example2:
同样的,这道题中的
K
∈
R
+
n
K \in R_+^n
K∈R+n,对于
x
2
x_2
x2,向量
a
⃗
\vec{a}
a并不在K中,所以
x
2
x_2
x2是极小值。
对于
x
3
x_3
x3,因为b在K中,所以
x
3
x_3
x3不是极小值。
5 分离与支撑超平面
5.1 超平面分离定理

几何直觉上很容易理解,先找到两个凸集的最近点,然后找到中点,确定法线,就定出了超平面。
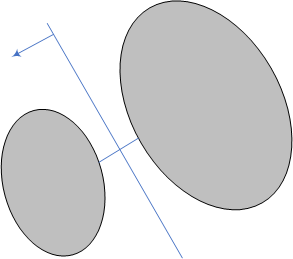
5.2 支撑超平面
进入支撑超平面的概念之前,先回顾超平面的概念。

下面红色的超平面
{
y
∣
a
T
y
=
a
T
x
0
}
\{y|a^Ty=a^Tx_0 \}
{y∣aTy=aTx0}为集合C在点
x
0
x_0
x0处的支撑超平面。
对于任意的C上的点
x
i
x_i
xi,有
a
T
x
i
≤
a
T
x
0
a^Tx_i\leq a^Tx_0
aTxi≤aTx0,即集合C上的点都在支撑超平面下方。

6 对偶锥与广义不等式
6.1 对偶锥定义
令K为一个锥,集合
K
∗
=
{
y
∣
x
T
y
≥
0
,
V
x
∈
K
}
K*=\{ y|x^Ty\geq 0, Vx \in K \}
K∗={y∣xTy≥0,Vx∈K}
称为K的对偶锥。
K是法线的集合,根据定义下面是一个典型的对偶锥。简易判断的方法是,法线对应的超平面,是否可以包络原集合K。

根据上面的图,即使原集合K不是凸集,对偶锥仍然是凸锥。对偶锥具有下列的性质
1)K是闭凸锥;
2)
K
1
⊆
K
2
,
则
K
2
∗
⊆
K
1
∗
K_1\subseteq K_2,则K_2^* \subseteq K_1^*
K1⊆K2,则K2∗⊆K1∗;
3) 如果K有非空内部,那么K是尖的;
4)如果K的闭包是尖的,那么K有非空内部;
5)K** 是K的凸包的闭包;
6.2 广义不等式的对偶
称广义不等式
⪯
K
∗
\preceq K^*
⪯K∗为广义不等式
⪯
K
\preceq K
⪯K的对偶,具有下列性质
1)
x
⪯
k
y
,
当
且
仅
当
任
意
λ
⪰
k
∗
0
,
有
λ
T
x
<
λ
T
y
x\preceq_k y,当且仅当任意 \lambda\succeq_{k^*} 0, 有\lambda^T x <\lambda^T y
x⪯ky,当且仅当任意λ⪰k∗0,有λTx<λTy
- 最小元的对偶性质
根据广义不等式对偶的性质,x是S上关于广义不等式 ⪯ K \preceq K ⪯K的最小元的充要条件是,对于所有 λ ≻ K ∗ 0 \lambda \succ_{K^*} 0 λ≻K∗0,x是在 z ∈ S z \in S z∈S上极小化 λ T z \lambda^T z λTz的唯一最优解。
从 几 何 上 看 , 对 于 任 意 λ ≻ K ∗ 0 , 超 平 面 { z ∣ λ T ( z − x ) = 0 } 是 在 x 处 对 S 的 一 个 严 格 支 撑 超 平 面 。 \color{red}{从几何上看,对于任意\lambda \succ_{K^*} 0,超平面\{ z|\lambda^T(z-x)=0 \}是在x处对S的一个严格支撑超平面。} 从几何上看,对于任意λ≻K∗0,超平面{z∣λT(z−x)=0}是在x处对S的一个严格支撑超平面。

- 极小元的对偶性质
如果 λ ≻ K ∗ 0 并 且 x 在 z ∈ S 上 极 小 化 λ T z , 那 么 x 是 极 小 的 。 \lambda \succ_{K^*}0并且x在z\in S上极小化\lambda^Tz,那么x是极小的。 λ≻K∗0并且x在z∈S上极小化λTz,那么x是极小的。
两者的区别是上图中的x使得所有的 λ T z 最 小 , z ∈ S \lambda^Tz最小,z \in S λTz最小,z∈S
下图中, x 1 使 得 λ 1 T z 最 小 , z ∈ S x_1使得\lambda_1^Tz最小, z \in S x1使得λ1Tz最小,z∈S, x 2 使 得 λ 2 T z 最 小 。 x_2使得\lambda_2^Tz最小。 x2使得λ2Tz最小。
























 2563
2563











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








