LearnOpenGL学习笔记—入门06 附：关于四元数

关于四元数

避免万向节死锁的真正解决方案是使用四元数(Quaternion)
本节关于四元数的理解以及它对三维旋转的作用，主要对3Blue1Brown的视频进行了描述和理解，可以从这两个视频找到它：四元数的可视化，四元数和三维转动
官方网站是这里，有互动视频可以实操一下。

1 四元数的可视化

这个视频中，3B1B给我们建立了直观印象，看四元数对四维空间都干了什么，以此来可以更好理解四元数的公式
视频中分了以下几个主题展开

• 1.怎样让一个只能理解一维的人来理解复数
• 2.向只能理解二维的人描述三维旋转
• 3.在三维的约束下，表现四元数在干什么

1.1 从一维到复数

假设一个一维人，“小莱”，它只能理解一维几何和实数，我们向他描述复数。
我们可以选择纯代数的方法来定义复数。

以及定义复数的乘法

但是这样，“小莱”并没有清楚复数的意义在几何和空间直觉，它那非常有用的作用究竟是什么。

1.1.1 左为变换作用，右为点

我们作为理解二维空间的人，可以这么理解复数乘法

• 如下图的Z·W，我们可以把Z看成是对这个平面的一个变换，1通过这个变换得到了Z，而0通过这个变换则没有改变
  
• 于是Z·W，是让W以及它所在的平面进行了这么个变换，得到了对应的结果，并且在二维空间中有且只有这一种拉伸旋转（Z这种变换）才能做到。
  

我们在接下来理解四元数乘法时，也需要用到这种思想，即左边是一个变换的“函数”，去变换右边的数，并且理解左边的这个“函数”，是怎么变换整个空间的。

对于复数是一种“作用”的理解，可以点击这里进行复习。

1.1.2 从一维看旋转？

现在回到“小莱”的身上，作为一维人的它，非常熟悉拉伸的变换，也就是实数的乘法。
多维上，每一维度的变换本质上没什么不同，“小莱”都可以理解，难的是如何和“小莱”介绍旋转。
比如复平面上的单位圆，上面的点到0的距离都是1，所以乘上这些点就对应着纯旋转，我们要如何对“小莱”解释这些复数乘法呢？

我们可能会觉得很难考虑，毕竟旋转是一个二维的东西。
但是旋转只有一个自由度，只有代表角度的数字，每一个角度唯一确定一个旋转。
所以所有二维旋转的集合可以把它映射到一维的数轴上，那里就是“小莱”的家。
如何进行映射，有很多方法，这次使用的是“球极投影”。
球极投影可以将圆映射到直线，球映射到平面，乃至四维超球到三维空间

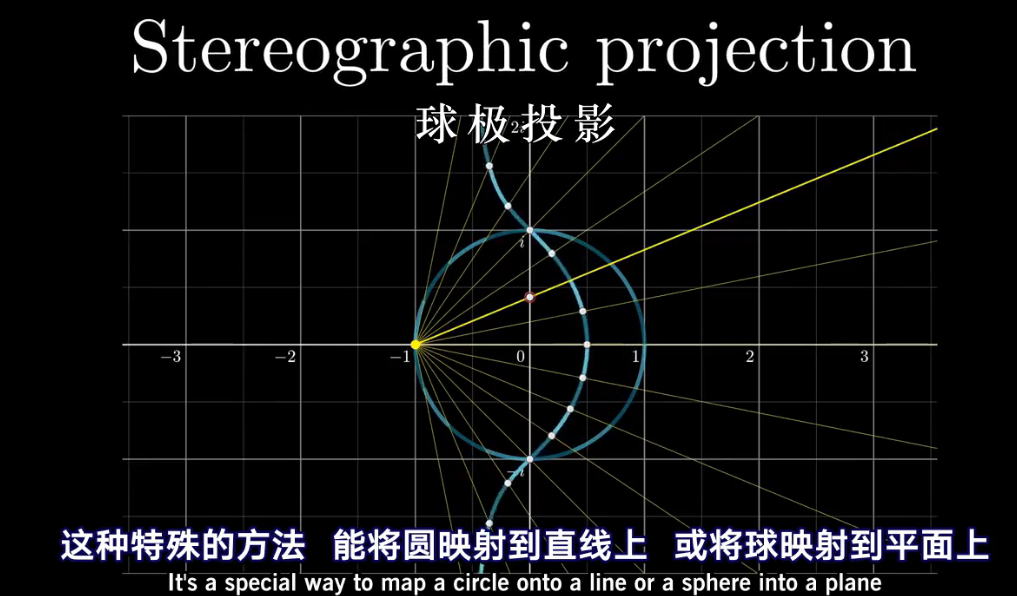
1.1.3 球极投影

从-1出发做直线，穿过单位圆上的每一个点，取这条线与纵轴的交点，这便是圆上的点被投影到的地方。

• 点1被映射到直线的中心保持不动，i与-i也是如此。
• 从i到1上这个90度上的所有的点，被映射到，1的对应点和i的对应点之间。
• i到-1这个圆弧上的点，则被映射到，i的对应点与正无穷之间。
• -1到i的圆弧上的点，则被映射到，-i的对应点与负无穷之间。
• -1本来不会映射到上面去，但是我们可以说，-1被映射到了无穷远的点上，无论沿着什么方向，走到无穷远就能看到-1对应的位置。

而这组由映射点组成的线，就是“小莱”能看懂的东西了。

这根线，仅仅是复数中距离原点长度为1的那些，即单位圆，其他的复数比如0,1+i,2等等，“小莱”并看不到。
但是没有关系，我们要做的，只是让“小莱”了解那些乘法中代表旋转的复数Z，所以只需要理解单位圆就可以了。
在圆上的旋转作用，映射到线上成为了变形的效果。

• i·1=i → 1这个点进行了i这个变换（逆时针90度），对应到线上，1这个位置的点移动到了i的位置上。
• i·i=-1 → i这个点进行了i这个变换（逆时针90度），对应到线上，i这个位置的点移动到了-1，即移动到了无穷远。
• i·-1=-i → -1这个点进行了i这个变换（逆时针90度），对应到线上，-1这个位置的点移动到了-i，即从无穷远移到了-i。
• i·-i=1 → -i这个点进行了i这个变换（逆时针90度），对应到线上，-i这个位置的点移动到了1的位置上。

虽然是有些奇怪的运动，但是我们依靠这个方法传达了一些思想，比如，被i连乘了四次，对应着转了4次90度，我们会回到原来的地方。

1.2 从二维到球体旋转

下面的这个纸片人“小菲”，它只能理解二维的几何，想象一下我们要如何向它解释球体的旋转

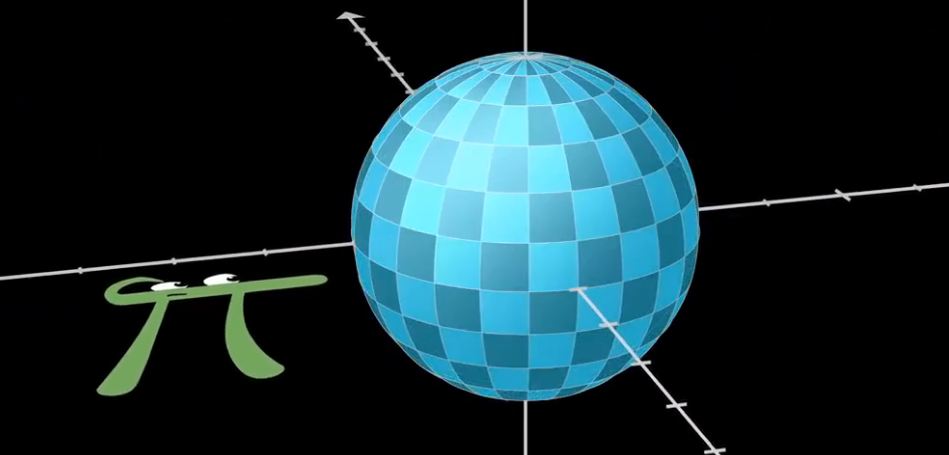
为了从二维的旋转过渡到四元数，我们拓展一下复数，在水平的实数轴和垂直的虚数轴上，加上第三条轴

我们让ij成为xy轴，实数轴则对应到Z轴的方向。

• 这时候三维空间中的点，都可以用一个实数，加上另一个实数乘以i，再加上另一个实数乘以j来表示，如1.25+1.5i±j。

然而想要为这样一个三维数系定义一个乘法概念，让它满足平时的代数性质来构造出有用的乘法，根据群论的知识，这样构造出来的乘法是不封闭的，所以我们无法定义。

我们想象一下向纸片人“小菲”描述这个坐标系中的三维旋转，单位球由所有到原点距离为1的数组成，即他们坐标的平方和为1。

我们无法把三维旋转给“小菲”看，但是我们可以把这个球的二维投影进行展示。
从南极处的-1开始，做一条直线穿过球上任意一点，这条线和ij平面的交点，就是球上该点的投影。

• 北极的1来到了平面中心，北半球的点映射到Ij平面上的单位圆内部。
• 通过i,j,-i,-j四点的单位圆映射后原地不动，这也是“小菲”和我们都能看见的，真实的单位球的一部分
• 所有南半球的点被映射到单位圆之外，同样的-1我们定义它被映射到无穷远

以下是映射图，粉色点代表北极旋转后的位置，黄色的圈代表赤道投影

我们可以关注于几个关键的参考点来识图追踪整个球体，
经过-i,1,i,-1的单位圆，映射到了“小菲”所在的 虚平面的 i轴
同时我们只是投影了单位球上的点，在三维真正的i轴上的点大部分是看不到
同样的我们把经过1,j,-1,-j的单位圆，映射到了“小菲”所在的 虚平面的 j轴

• 通过推理可以知道，“小菲”所在的平面上任意一个直线，都是在球面上过-1的圆的投影，某种意义上说，所有直线都是一个过无穷远的圆
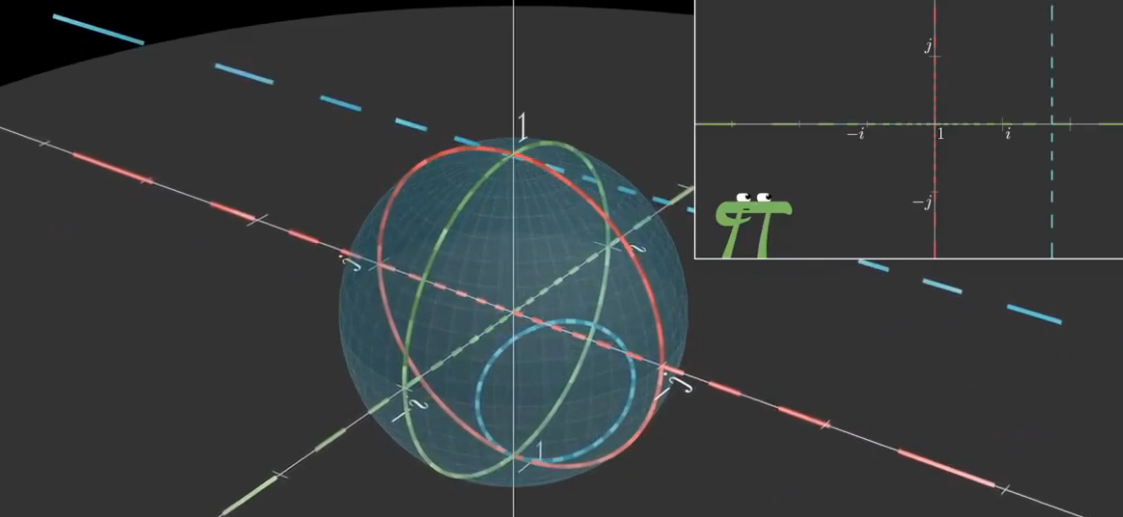
• 想象一下在“小菲”的视角中，把球体绕j轴旋转，我们把ij单位圆转到1j的单位圆
  在小菲的眼中就是，黄色的单位圆变成了垂直线，而红色的线变成了单位圆
  
  我们看到的是旋转的运动，在“小菲”看来，就是比较扭曲的投影效果，从单位圆到水平直线的变化

1.3 三维人看四元数

1.3.1 四元数

复数有一个虚部，不存在的“三维复数”有两个虚部，四元数则有三个虚数维度

这三个虚数维度都和实数轴垂直，同时它们自己也互相垂直

四元数有四个实数，可以把它拆解成一个实部/标量，加上一个三维的虚部。
这个三维的虚部，即没有标量部分的四元数，也就是向量（vector）。
我们可以直接定义出四元数乘法，给出ijk的乘法规则，规定它们满足分配律的方式。
这也是我们告诉计算机来算四元数的方式。

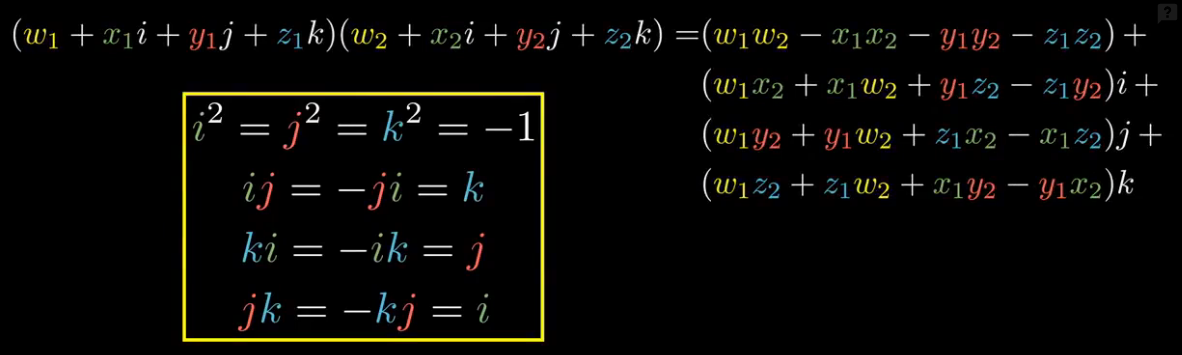
对于矩阵乘法，四元数乘法更加简洁，所以它在图形学编程和其他领域十分有用。
我们也可以用点积和叉积的形式来表示

1.3.2 四元数的球极投影

但是正如深入理解复数乘法需要理解它的几何意义——乘一个复数代表进行了一个缩放与旋转的变换，我们需要明白四元数乘法的四维几何意义。
与二维类似，四维上的点到原点的距离，依然是每个分量进行平方和后的平方根。
四元数乘法，我们可以理解为，先对四元数进行了放缩，然后进行旋转。
这个特殊的四维旋转规则，就是我们要理解的内容。
（下图字幕应为放大q2到q1）

与之对应的是到远点距离为1的四元数组成的四维超球，与之前从一维理解旋转，到二维理解球体，如今我们需要用三维理解四元数。
不仅仅是因为，四维单位超球上的点的乘法是纯粹的四维旋转，而且也因为我们可以跟踪四维超球上的一些点，来理解这种四维作用，而不需要去理解整个四维空间的所有点。

就像之前的投影，我们把四维超球投影到三维空间来。
按照之前的规律，1这个点，来到了投影空间的正中

并且正如

• 投影过后，在i这个轴上的点，在线人“小莱”的空间保持不变，即实部为0，虚部的部分
• 投影过后，在ij平面的单位圆，在纸片人“小菲”的空间保持不变，即实部为0，虚部的部分

那么投影过后，在ijk空间的单位球，在我们三维人的空间保持不变
所以我们在三维空间看到的单位球，代表着四维超球投影到我们空间时，不变的那一部分，即实部为0，虚部的部分。

这个单位球代表着四维超球上所有实部为0的四元数，也被数学界称为单位向量

• 那些实部为0到1的单位四元数，投影到了球的内部，靠近中央的1
• 实部从-1到0的单位四元数，则投影到球的外部
• -1这个点坐落在无穷远处，从任意一个方向都能走到
• 整个三维空间，都是一个四维单位超球的投影，只包括了满足四个分量的平方和等于1的四元数。
  所以三维空间上的每一点，所对应的四元数都有着同样的模，即在四维，它到0的距离都是1。
• 除此以外的其他四元数，我们看不到
• 与之前纸片人一样，每一个线，代表了一个过-1的圆
• 每一个平面，代表了四维超球上的一个三维球
• 如果他正好是通过了1,i,j,-i,-j,以及-1的三维球，那么他就会被投影到我们所谓的xy平面
• 正如同过-1和1的圆，变成了过中心的所有直线→过-1,1的三维球的投影，就是过中心的所有平面。
• 由此也知道了，所有平面，都是四维单位超球上，过-1的三维球的投影。

1.3.3 四元数的乘法

现在取一个单位四元数，左乘另一个四元数，这种作用可以被理解为，两个独立的二维旋转，互相垂直，同时发生。

• 第一个例子 i乘以一个四元数
  我们已经知道，i·1=i，也就是一维上，1这个点，会运动到i的位置（二维上的含义是，1这个点旋转到i），同样的i·i=-1等等
  我们把他们看成数轴上的运动，1移到i，移到无穷远，移到-i，移回1
  在上文“小莱”部分已经讲过，不再赘述
  即数轴的移动，代表了经过球极投影的，在一个平面内的旋转
  
• 我们再来看通过j,k的圆，它垂直于通过1,i的圆（因为四维每两个面都互相垂直）
  我们把这个通过1,i的圆，投影变成了一条直线（因为这个圆在实数轴和i轴的平面里，二维到一维投影完就是i轴，在四维到三维的投影中依然是i轴）。
  在虚平面上的j,k圆，依然像个圆，但是复平面上的圆，就是一个线了。
  所以以下是，两个圆的投影图
  
• 这就形成了一种很像右手定则的东西。
  在这里我们先缓一下
  一个二维的旋转，是两个互相垂直同时发生的一维的旋转
  一个三维的旋转，也可以看成三个一维的旋转，或者一个二维的平面旋转加上一个一维旋转（如欧拉角）
  一个四维旋转，可以看成两个互相垂直同时发生的二维旋转。
  即上图中的两个投影出来的互相垂直的圆，同时发生旋转，一个在转，一个在数轴上移动
  （为什么不选其他两个虚轴的圆呢，因为那样就没有右手定则似的东西了嘛~）
• 所以此时我们再看四元数的乘法法则
  i·j=k 对j应用 i这个四元数旋转 会得到k
  拆解成刚才的图，红圈j点转到k点转了90度，并且底下的线也进行90度代表的移动
  i·k=-j i·-j=-k i·-k=j
• 从计算方面
  如果我们知道了一个四元数对1,i,j,k会做什么，那么我们也就知道了它会对任意四元数做什么，因为满足分配律。
  线性代数的方法来说就是，1 i j k是四维空间的基，我们知道了对基的变换，也就知道了这个空间的变换。（线性代数也可以去看3b1b大佬的视频）

几何上，一个四维生物可以看到这个两个互相垂直的旋转的作用效果，并且它能知道这两个旋转唯一确定了一个四维超球的刚体运动。
到三维的投影就是一个球被里外里外的翻转了（在移动放大的同时在转）
经过四次迭代会回到原来的位置

比如对下图中手旁边的这个四元数（注意，这是被投影过的，所以是数轴上的点，它本来是实轴和i轴这个复平面上的点）
这个四元数给其他乘上它的四元数所带来的变换，在我们看来是把1拉到它这个位置的投影，并且jk圆按照右手法则旋转了135度。

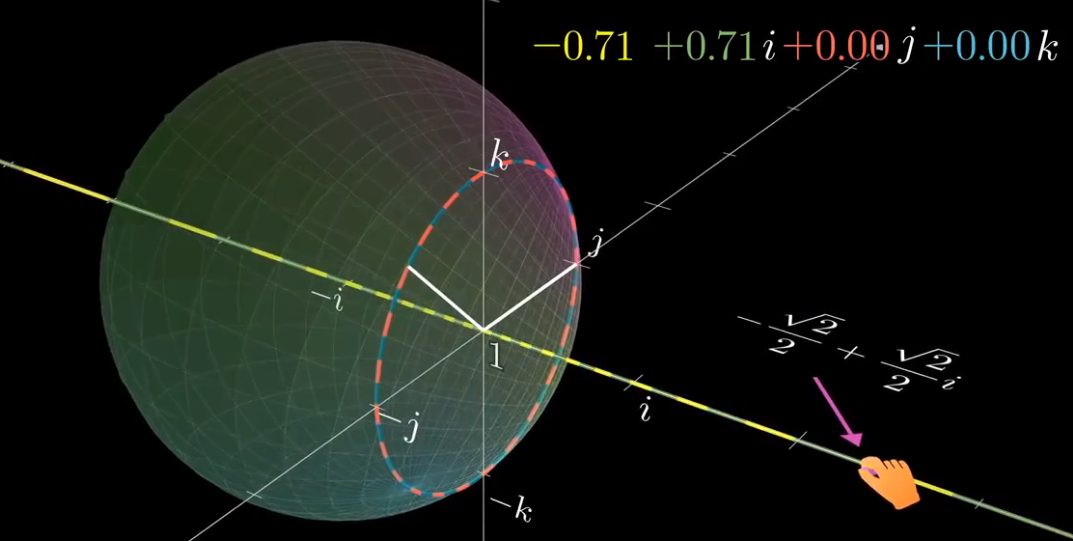
再比如j来左乘，1这个点要移到j，
对应的j轴代表的圆，它会有个垂直的圆在ik上
1到j，然后ik圆右手定则，产生了k到i的90度旋转
投影从三维球被拉成了一个平面
因为j·1=j k·i=j 这两个垂直方向上在同时进行，这样才能确定一个四元数的旋转

• 通过右手定则，可以看着这个虚轴的3d图，把乘法规则记下来。
  比如j·i=?
  对i进行j的变换，我们先看看j的变换代表什么
  从1到j，右手定则i会被移动到-k，即这个变换的结果是-k
  所以j·i=-k.
• 这也意味着，四元数上乘法没有交换律
  类比来说，旋转也没有交换律

对于任意的单位四元数q
首先我们在四维空间画一个过1 q -1的圆，对应过来就是一个过原点的直线
然后在单位球上画一个垂直它的单位圆
旋转这个圆，并且让1带动拉伸到q，这就是这个四元数代表的变换。

目前展示了把四元数作为左乘作用的理解方式，即把i视为一个函数，扭曲了整个空间，j只是一个点

但是如果用右乘的方式来理解，就要用到左手了，理解左手的法则，对于如何用单位四元数描述三维旋转很有用，这也是下一节的内容。

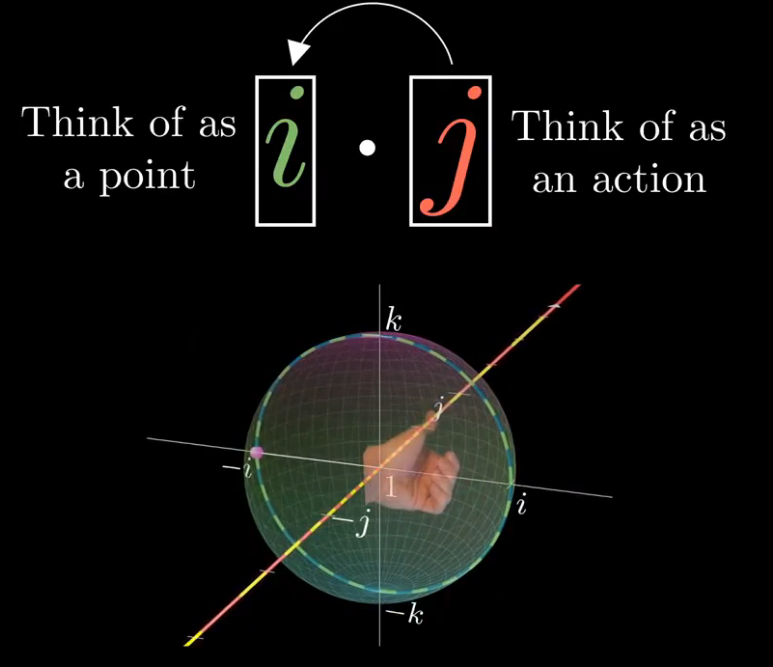
2 四元数与三维转动

在上一节结束后，可能会怀疑，为什么要发明这种数学体系，和外星人用的一样。
其实它对描述3d方位提供了一个很好的方法，而不会受到其他方法带来的错误以及边界效应。
其他方法描述旋转也有，而且易于想像，比如线性代数的旋转矩阵，并且我们构建旋转矩阵时，往往是想像三根垂直的柱子，他们的旋转角也被叫做欧拉角

它的问题是万向节锁，也就是两条旋转轴重合时，系统会失去一个自由度，并且在两个不同方向上插值的时候，也会造成困难（关于这些问题网上也有很多资源描述）
四元数不仅避免了万向节锁，而且也提供了三维方位中插值的平滑方法，避免了欧拉角的歧义，也避免了两个旋转矩阵中插值会出现的数值精度和整化问题。
下面开始介绍用用四元数描述旋转

• 首先用一个单位向量定义想要旋转的这个轴，并且i j k 归一化处理，平方和为1
• 用想要旋转的角构建四元数q，用半角的余弦作为实部，半角的正弦乘上虚部
• 取一个三维点p，用i j k表示，如果想知道将这个点绕某个轴旋转某个角度以后会出现在哪里
  那么我们会用$q\cdot p\cdot q^{-1}$，展开算式就是结果了
  
  
  强烈建议去视频它推荐的那个互动视频去实操一遍

2.1 公式如何产生？

我们知道，一个单位四元数代表的变换，可以拆分成这个三维投影球的旋转与垂直方向的拉伸两个部分，我们需要把旋转部分拿出来，而不进行拉伸。
提到旋转就会想到角度与三角函数，而三角函数和复数的关系，我们就想到了欧拉公式。

首先利用欧拉公式对四元数进行推广

• 欧拉公式在复变函数中的证明，是从$e^x$的麦克劳林公式中，把$x$换成$ix$，然后根据$i$的运算规则与$cos$和$sin$的麦克劳林公式，证明得到 e i x = c o s x + i s i n x e^ix=cosx+isinx e