计算矩阵的逆源码（使用伴随矩阵，3×3的矩阵）

目的：最近写C++代码，遇到求矩阵的逆。Eigen库有方法计算。但是因为再求导过程中，需要求逆的具体方式。因此自己实现了求矩阵的逆。具体代码如下，对于公式部分后续再补，更新。

//更新公式部分
维基百科的定义：
在线性代数中，一个方形矩阵的伴随矩阵（英语：adjugate matrix）是一个类似于逆矩阵的概念。如果矩阵可逆，那么它的逆矩阵和它的伴随矩阵之间只差一个系数。然而，伴随矩阵对不可逆的矩阵也有定义，并且不需要用到除法。
假设$\mathbf{A}$的伴随矩阵记作$adj(\mathbf{A})$或者${\mathbf{A}}^{\ast }$
因为在项目中通常需要$3\times 3$的矩阵，它可以定义为：
$$\mathbf{A}=\left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right]$$

它的伴随矩阵是：

$$adj(\mathbf{A})=\left[\begin{array}{ccc}+\left|\begin{array}{cc}{a}_{22}& a_{23}\\ a_{32}& a_{33}\end{array}\right|& -\left|\begin{array}{cc}{a}_{12}& a_{13}\\ a_{32}& a_{33}\end{array}\right|& +\left|\begin{array}{cc}{a}_{12}& a_{13}\\ a_{22}& a_{23}\end{array}\right|\\ & & \\ -\left|\begin{array}{cc}{a}_{21}& a_{23}\\ a_{31}& a_{33}\end{array}\right|& +\left|\begin{array}{cc}{a}_{11}& a_{13}\\ a_{31}& a_{33}\end{array}\right|& -\left|\begin{array}{cc}{a}_{11}& a_{13}\\ a_{21}& a_{23}\end{array}\right|\\ & & \\ +\left|\begin{array}{cc}{a}_{21}& a_{22}\\ a_{31}& a_{32}\end{array}\right|& -\left|\begin{array}{cc}{a}_{11}& a_{12}\\ a_{31}& a_{32}\end{array}\right|& +\left|\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right|\end{array}\right]$$

其中
$$\left|\begin{array}{cc}{a}_{im}& a_{in}\\ a_{jm}& a_{jn}\end{array}\right|=det\left[\begin{array}{cc}{a}_{im}& a_{in}\\ a_{jm}& a_{jn}\end{array}\right]=det\left|\begin{array}{cc}{a}_{im}& a_{in}\\ a_{jm}& a_{jn}\end{array}\right|$$

从上面公式可以看出，伴随矩阵是余因子矩阵的转置。

伴随矩阵可以用来计算矩阵的逆：
$${\mathbf{A}}^{-1}=\frac{adj(\mathbf{A})}{det(\mathbf{A})}=\frac{{\mathbf{A}}^{\ast }}{|\mathbf{A}|}$$
其中${\mathbf{A}}^{\ast }$为伴随矩阵；$|\mathbf{A}|$为矩阵的行列式。

其中行列式计算可以参考我的blog
https://blog.csdn.net/weixin_43851636/article/details/125999210?spm=1001.2014.3001.5502

下面是通过伴随矩阵计算矩阵的逆的C++代码，它和Eigen库中的求逆一样。

c++代码

#include<Eigen/Eigen>
#include<iostream>
#include<vector>
#include<string>

/*
m=[n1,
   n2,
   n3]
*/
Eigen::Matrix3f ConstructMatrix3fFromVectors(Eigen::Vector3f& n1, Eigen::Vector3f& n2, Eigen::Vector3f& n3)
{
    Eigen::Matrix3f m;
    m.block<1, 3>(0, 0) = n1;
    m.block<1, 3>(1, 0) = n2;
    m.block<1, 3>(2, 0) = n3;
    return m;
}

Eigen::Matrix3f ConstructAdjugateMatrix3f(Eigen::Matrix3f& m)
{
    Eigen::Matrix3f adju_m;
    adju_m(0, 0) = m(1, 1)*m(2, 2) - m(2, 1)*m(1, 2);
    adju_m(0, 1) = -(m(0, 1)*m(2, 2) - m(2, 1)*m(0, 2));
    adju_m(0, 2) = m(0, 1)*m(1, 2) - m(1, 1)*m(0, 2);
    adju_m(1, 0) = -(m(1, 0)*m(2, 2) - m(2, 0)*m(1, 2));
    adju_m(1, 1) = m(0, 0)*m(2, 2) - m(2, 0)*m(0, 2);
    adju_m(1, 2) = -(m(0, 0)*m(1, 2) - m(1, 0)*m(0, 2));
    adju_m(2, 0) = m(1, 0)*m(2, 1) - m(2, 0)*m(1, 1);
    adju_m(2, 1) = -(m(0, 0)*m(2, 1) - m(2, 0)*m(0, 1));
    adju_m(2, 2) = m(0, 0)*m(1, 1) - m(1, 0)*m(0, 1);
    return adju_m;
}

Eigen::Vector3f ComputeKVector(Eigen::Matrix3f& adjm, Eigen::Vector3f& b)
{
    Eigen::Vector3f k;
    k = adjm*b;
    return k;
}

//test adjugate matrix

int main(int argc, char** argv)
{
    Eigen::Vector3f n1 = Eigen::Vector3f(1, 2, 3);
    Eigen::Vector3f n2 = Eigen::Vector3f(2, 1, 3);
    Eigen::Vector3f n3 = Eigen::Vector3f(2, 2, 1);
    Eigen::Matrix3f m = ConstructMatrix3fFromVectors(n1, n2, n3);
    Eigen::Matrix3f m_i = m.inverse();
    std::cerr << "m_i: \n" << m_i << std::endl;
    Eigen::Matrix3f adju_m = ConstructAdjugateMatrix3f(m);
    float det = m.determinant();
    Eigen::Matrix3f m_i_my = adju_m/det;
    std::cerr << "m_i_my: \n" << m_i_my << std::endl;

    std::cerr<<"end test..."<<std::endl;
    return 0;
}

运行的结果如下：它和eigen计算一样的。

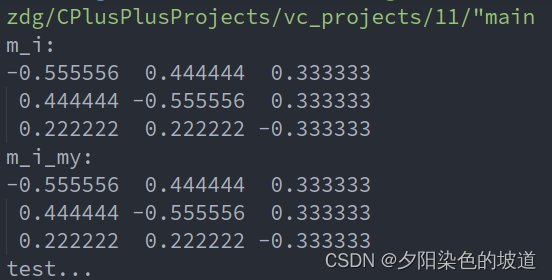
贴上维基百科的超链接为：
https://zh.m.wikipedia.org/zh-sg/%E4%BC%B4%E9%9A%8F%E7%9F%A9%E9%98%B5