目标:最近在看论文,需要一些基本的公式推理,经常遇到三重积的等式。为了更深入的理解。因此推导一下这类公式。
定义:
向量三重积
a
→
×
(
b
→
×
c
→
)
=
(
a
→
⋅
c
→
)
⋅
b
→
−
(
a
→
⋅
b
→
)
⋅
c
→
\overrightarrow{a} \times (\overrightarrow{b} \times \overrightarrow{c})= (\overrightarrow{a} \cdot \overrightarrow{c}) \cdot\overrightarrow{b} - (\overrightarrow{a} \cdot \overrightarrow{b}) \cdot\overrightarrow{c}
a×(b×c)=(a⋅c)⋅b−(a⋅b)⋅c
其中 a → = ( a 0 , a 1 , . . . , a n ) \overrightarrow{a}=(a_0,a_1,...,a_n) a=(a0,a1,...,an); b → = ( b 0 , b 1 , . . . , b n ) \overrightarrow{b}=(b_0,b_1,...,b_n) b=(b0,b1,...,bn); c → = ( c 0 , c 1 , . . . , c n ) \overrightarrow{c}=(c_0,c_1,...,c_n) c=(c0,c1,...,cn)
在空间向量中一般 n = 3 n=3 n=3
证明,它有两种方法可以证明
第一种是最简单的方式,直接展开左右两边的项。
对于叉乘一般情况下是可以转化为矩阵和向量的乘积。转化表示为下面
S
k
e
w
(
a
)
=
[
0
−
a
2
a
1
a
2
0
−
a
0
−
a
1
a
0
0
]
Skew(a) = \begin{bmatrix} 0 \space \space -a_2 \space \space a_1 \\ a_2 \space \space 0 \space \space -a_0 \\ -a_1 \space \space a_0 \space \space 0 \end{bmatrix}
Skew(a)=⎣
⎡0 −a2 a1a2 0 −a0−a1 a0 0⎦
⎤
因此得到左边公式为:
a
→
×
(
b
→
×
c
→
)
=
s
k
e
w
(
a
→
)
(
s
k
e
w
(
b
→
)
c
→
)
=
[
0
−
a
2
a
1
a
2
0
−
a
0
−
a
1
a
0
0
]
[
0
−
b
2
b
1
b
2
0
−
b
0
−
b
1
b
0
0
]
[
c
0
c
1
c
2
]
=
[
0
−
a
2
a
1
a
2
0
−
a
0
−
a
1
a
0
0
]
[
b
1
c
2
−
b
2
c
1
b
2
c
0
−
b
0
c
2
b
0
c
1
−
b
1
c
0
]
=
[
−
a
2
(
b
2
c
0
−
b
0
c
2
)
+
a
1
(
b
0
c
1
−
b
1
c
0
)
a
2
(
b
1
c
2
−
b
2
c
1
)
−
a
0
(
b
0
c
1
−
b
1
c
0
)
−
a
1
(
b
1
c
2
−
b
2
c
1
)
+
a
0
(
b
2
c
0
−
b
0
c
2
)
]
=
[
(
a
1
c
1
+
a
2
c
2
)
b
0
−
(
a
1
b
1
+
a
2
b
2
)
c
0
(
a
0
c
0
+
a
2
c
2
)
b
1
−
(
a
0
b
0
+
a
2
b
2
)
c
1
(
a
0
c
0
+
a
1
c
1
)
b
2
−
(
a
0
b
0
+
a
1
b
1
)
c
2
]
=
[
(
a
0
c
0
+
a
1
c
1
+
a
2
c
2
)
b
0
−
(
a
0
b
0
+
a
1
b
1
+
a
2
b
2
)
c
0
(
a
0
c
0
+
a
1
c
1
+
a
2
c
2
)
b
1
−
(
a
0
b
0
+
a
1
b
1
+
a
2
b
2
)
c
1
(
a
0
c
0
+
a
1
c
1
+
a
2
c
2
)
b
2
−
(
a
0
b
0
+
a
1
b
1
+
a
2
b
2
)
c
2
]
=
(
a
→
⋅
c
→
)
⋅
b
→
−
(
a
→
⋅
b
→
)
⋅
c
→
\overrightarrow{a} \times (\overrightarrow{b} \times \overrightarrow{c}) \\ =skew(\overrightarrow{a})(skew(\overrightarrow{b})\overrightarrow{c}) \\ = \begin{bmatrix} 0 \space \space -a_2 \space \space a_1 \\ a_2 \space \space 0 \space \space -a_0 \\ -a_1 \space \space a_0 \space \space 0 \end{bmatrix} \begin{bmatrix} 0 \space \space -b_2 \space \space b_1 \\ b_2 \space \space 0 \space \space -b_0 \\ -b_1 \space \space b_0 \space \space 0 \end{bmatrix} \begin{bmatrix} c_0 \\ c_1 \\ c_2 \end{bmatrix} =\begin{bmatrix} 0 \space \space -a_2 \space \space a_1 \\ a_2 \space \space 0 \space \space -a_0 \\ -a_1 \space \space a_0 \space \space 0 \end{bmatrix} \begin{bmatrix} b_1c_2-b_2c_1 \\ b_2c_0-b_0c_2 \\ b_0c_1-b_1c_0 \end{bmatrix} \\ \\ =\begin{bmatrix} -a_2(b_2c_0-b_0c_2) + a_1(b_0c_1-b_1c_0) \\ a_2(b_1c_2-b_2c_1) - a_0(b_0c_1-b_1c_0) \\ -a_1(b_1c_2-b_2c_1) + a_0(b_2c_0-b_0c_2) \end{bmatrix} = \begin{bmatrix} (a_1c_1+a_2c_2)b_0 - (a_1b_1+a_2b_2)c_0 \\ (a_0c_0+a_2c_2)b_1 - (a_0b_0+a_2b_2)c_1 \\ (a_0c_0+a_1c_1)b_2 - (a_0b_0+a_1b_1)c_2 \end{bmatrix} \\ = \begin{bmatrix} (a_0c_0+a_1c_1+a_2c_2)b_0 - (a_0b_0+a_1b_1+a_2b_2)c_0 \\ (a_0c_0+a_1c_1+a_2c_2)b_1 - (a_0b_0+a_1b_1+a_2b_2)c_1 \\ (a_0c_0+a_1c_1+a_2c_2)b_2 - (a_0b_0+a_1b_1+a_2b_2)c_2 \end{bmatrix} = (\overrightarrow{a} \cdot \overrightarrow{c}) \cdot\overrightarrow{b} - (\overrightarrow{a} \cdot \overrightarrow{b}) \cdot\overrightarrow{c}
a×(b×c)=skew(a)(skew(b)c)=⎣
⎡0 −a2 a1a2 0 −a0−a1 a0 0⎦
⎤⎣
⎡0 −b2 b1b2 0 −b0−b1 b0 0⎦
⎤⎣
⎡c0c1c2⎦
⎤=⎣
⎡0 −a2 a1a2 0 −a0−a1 a0 0⎦
⎤⎣
⎡b1c2−b2c1b2c0−b0c2b0c1−b1c0⎦
⎤=⎣
⎡−a2(b2c0−b0c2)+a1(b0c1−b1c0)a2(b1c2−b2c1)−a0(b0c1−b1c0)−a1(b1c2−b2c1)+a0(b2c0−b0c2)⎦
⎤=⎣
⎡(a1c1+a2c2)b0−(a1b1+a2b2)c0(a0c0+a2c2)b1−(a0b0+a2b2)c1(a0c0+a1c1)b2−(a0b0+a1b1)c2⎦
⎤=⎣
⎡(a0c0+a1c1+a2c2)b0−(a0b0+a1b1+a2b2)c0(a0c0+a1c1+a2c2)b1−(a0b0+a1b1+a2b2)c1(a0c0+a1c1+a2c2)b2−(a0b0+a1b1+a2b2)c2⎦
⎤=(a⋅c)⋅b−(a⋅b)⋅c
证明完毕。
第二种方法: 具有几何意义的方式。它具有启发式的那种。建议使用这种方式来证明上面的三重积的等式。
为了能够方便大家理解,画出图像,得到下图
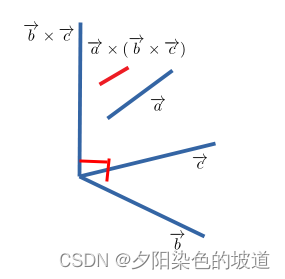
因为叉乘的积,是两个向量的垂直向量。比如
b
→
×
c
→
\overrightarrow{b} \times \overrightarrow{c}
b×c,它是垂直于
b
→
,
c
→
\overrightarrow{b},\overrightarrow{c}
b,c的两个向量所在的平面。
同时任意的向量
a
→
\overrightarrow{a}
a和
b
→
×
c
→
\overrightarrow{b} \times \overrightarrow{c}
b×c叉乘。得到的向量一定是平行于
b
→
,
c
→
\overrightarrow{b},\overrightarrow{c}
b,c的两个向量所在的平面。(红色的线段表示)。因此可以写成如下:
a
→
×
(
b
→
×
c
→
)
=
m
b
→
+
n
c
→
\overrightarrow{a} \times (\overrightarrow{b} \times \overrightarrow{c})=m\overrightarrow{b}+n\overrightarrow{c}
a×(b×c)=mb+nc
因为红色向量
a
→
×
(
b
→
×
c
→
)
\overrightarrow{a} \times (\overrightarrow{b} \times \overrightarrow{c})
a×(b×c)和
a
→
\overrightarrow{a}
a垂直。因此:
a
→
⋅
(
a
→
×
(
b
→
×
c
→
)
)
=
0
=
>
a
→
⋅
(
m
b
→
+
n
c
→
)
=
0
=
>
m
(
a
→
⋅
b
→
)
+
n
(
a
→
⋅
c
→
)
=
0
\overrightarrow{a} \cdot(\overrightarrow{a} \times (\overrightarrow{b} \times \overrightarrow{c})) = 0 \\ =>\overrightarrow{a} \cdot(m\overrightarrow{b}+n\overrightarrow{c}) = 0 \\ =>m(\overrightarrow{a} \cdot \overrightarrow{b}) + n(\overrightarrow{a} \cdot \overrightarrow{c})=0
a⋅(a×(b×c))=0=>a⋅(mb+nc)=0=>m(a⋅b)+n(a⋅c)=0
为了解决上面的公式,我们使用构造法,构造两个数使得上面的公式成立。构造如下:
存在
p
∈
R
p\in R
p∈R;且
m
=
p
(
a
→
⋅
c
→
)
m=p(\overrightarrow{a} \cdot \overrightarrow{c})
m=p(a⋅c);
n
=
−
p
(
a
→
⋅
b
→
)
n=-p(\overrightarrow{a} \cdot \overrightarrow{b})
n=−p(a⋅b),使得上面的公式恒成立。为了方便理解,构造的项带入公式
m
(
a
→
⋅
b
→
)
+
n
(
a
→
⋅
c
→
)
=
0
m(\overrightarrow{a} \cdot \overrightarrow{b}) + n(\overrightarrow{a} \cdot \overrightarrow{c})=0
m(a⋅b)+n(a⋅c)=0
m
(
a
→
⋅
b
→
)
+
n
(
a
→
⋅
c
→
)
=
0
=
p
(
a
→
⋅
c
→
)
(
a
→
⋅
b
→
)
−
p
(
a
→
⋅
b
→
)
(
a
→
⋅
c
→
)
=
0
m(\overrightarrow{a} \cdot \overrightarrow{b}) + n(\overrightarrow{a} \cdot \overrightarrow{c})=0 \\ =p(\overrightarrow{a} \cdot \overrightarrow{c})(\overrightarrow{a} \cdot \overrightarrow{b})-p(\overrightarrow{a} \cdot \overrightarrow{b})(\overrightarrow{a} \cdot \overrightarrow{c})=0
m(a⋅b)+n(a⋅c)=0=p(a⋅c)(a⋅b)−p(a⋅b)(a⋅c)=0
代入的等式可以看到上面是一个中恒等式。
上面的等式与向量
a
→
\overrightarrow{a}
a,
b
→
\overrightarrow{b}
b,
c
→
\overrightarrow{c}
c取值无关。
因此将
m
=
p
(
a
→
⋅
c
→
)
m=p(\overrightarrow{a} \cdot \overrightarrow{c})
m=p(a⋅c);
n
=
−
p
(
a
→
⋅
b
→
)
n=-p(\overrightarrow{a} \cdot \overrightarrow{b})
n=−p(a⋅b),代入到
a
→
×
(
b
→
×
c
→
)
=
m
b
→
+
n
c
→
\overrightarrow{a} \times (\overrightarrow{b} \times \overrightarrow{c})=m\overrightarrow{b}+n\overrightarrow{c}
a×(b×c)=mb+nc,得到如下公式:
a
→
×
(
b
→
×
c
→
)
=
m
b
→
+
n
c
→
=
p
(
a
→
⋅
c
→
)
b
→
−
p
(
a
→
⋅
b
→
)
c
→
\overrightarrow{a} \times (\overrightarrow{b} \times \overrightarrow{c})=m\overrightarrow{b}+n\overrightarrow{c}=p(\overrightarrow{a} \cdot \overrightarrow{c})\overrightarrow{b}-p(\overrightarrow{a} \cdot \overrightarrow{b})\overrightarrow{c}
a×(b×c)=mb+nc=p(a⋅c)b−p(a⋅b)c
因为上面公式和向量
a
→
\overrightarrow{a}
a,
b
→
\overrightarrow{b}
b,
c
→
\overrightarrow{c}
c无关,可以采用简单的向量
a
→
=
[
1
,
1
,
1
]
\overrightarrow{a}=[1,1,1]
a=[1,1,1];
b
→
=
[
0
,
1
,
0
]
\overrightarrow{b}=[0,1,0]
b=[0,1,0];
c
→
=
[
0
,
0
,
1
]
\overrightarrow{c}=[0,0,1]
c=[0,0,1]
带入相应的简单的公式,就可以得到
p
=
1
p=1
p=1
证明完毕。
参考资料如下:
https://www.youtube.com/watch?v=4U5fkwYDvZg























 309
309

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








