【SPH】DFSPH算法详解--1跟着paper学原理

前言

DFSPH是目前图形学领域最新最快的压力求解SPH算法，值得被首先关注。

我们将分为三部分来讲解DFSPH

1. 学原理：论文讲解
2. 读代码：splishsplash源码剖析
3. 动手实践：在taichi上从零开始实践该算法

本文属于学原理

---

DFSPH 原理

在原理方面，参考文献为（摘抄自Splishsplash)：

• [BK15] Jan Bender and Dan Koschier. Divergence-free smoothed particle hydrodynamics. In ACM SIGGRAPH / Eurographics Symposium on Computer Animation, SCA '15, 147-155. New York, NY, USA, 2015. ACM. URL: http://doi.acm.org/10.1145/2786784.2786796

• [BK17] Jan Bender and Dan Koschier. Divergence-free SPH for incompressible and viscous fluids. IEEE Transactions on Visualization and Computer Graphics, 23(3):1193-1206, 2017. URL:http://dx.doi.org/10.1109/TVCG.2016.2578335

• [KBST19] Dan Koschier, Jan Bender, Barbara Solenthaler, and Matthias Teschner. Smoothed particle hydrodynamics for physically-based simulation of fluids and solids. In Eurographics 2019 - Tutorials. Eurographics Association, 2019. URL: https://interactivecomputergraphics.github.io/SPH-Tutorial

参考网站（就是第三个参考文献里的，里面还包含了PPT）
https://interactivecomputergraphics.github.io/SPH-Tutorial/

我们今天就关注第一篇论文，就是Jan Bender & Dan Koschier 2015年发表的论文。这是最早的文献。

所谓DFSPH算法，关注的是如何快速求解压力。

首先从NS方程入手
$$\nabla \cdot v=0$$
$$Dv/Dt=-（1/\rho ）\nabla p+\nu {\nabla }^{2}v+f/\rho$$

上面NS方程组，未知量是v。但是我们不知道的还有两个量：密度和压力。

两者是相互关联的。求出一个，就能求出另一个。但是关联的关系并不是显式的，而是很复杂的。此外，我们发现两个方程是很难联立解的。一种办法就是把第一个方程改造改造，带入到第二个方程里。

怎么改造第一个方程呢？我们不妨改造改造，把它当作一种限制条件好了。由于它恰好是“速度的散度等于0”这一数学含义。我们就称这种限制条件为无散度条件。下面我们会详细讲怎么改造。改造之后，我们的第一个方程（连续性方程）将变换为关于压力的方程，被称为压力泊松方程（PPE）。这是重点1。

另一方面，怎么把另一个未知量密度改造一下呢？我们知道，在不可压缩流体之中（大致认为速度<30%音速的流体为不可压缩的），密度是不可能改变的。所以我们应该限制密度，这种限制条件被称为常密度条件。

于是我们就把压力和密度这两个未知量改造成了两个限制条件。

1. 无散度条件–压力
2. 常密度条件–密度

施加这两个条件，都会造成一些代价。在流体力学中，这个代价就是引入数值上的代价。

无散度条件：造成体积损失
常密度条件：造成密度震荡

体积损失的原因：首先，无散度条件即速度的散度为0。而速度的散度恰好就是体积增量。（如果不明白，想想高斯定理。如果还不明白，想象一个正方体，它的六个面都向外有通量，而为了保证质量守恒净通量一定为0，也就是进出动态平衡。）而在施加限制条件的时候，一定会造成某些数值上的截断误差，这些误差会随着迭代不断积累，要么造成体积增大了，要么造成体积减少了。而一般是体积减少（因为体积增大是不能忍受的，空间中不能凭空产生物质，宁可减少也不能增大）。

密度震荡原因：这个好理解。就是因为你在限定的时候，一定会出现超调的情况。比如我想要密度为1000，而现在密度为1200，那么我就减少他。但是减少多少是很难把控的。例如我乘以0.8，就得到了960，就导致调的过小了。于是再次调大，乘以1.05，得到1008。如此往复，虽然有时候能够震荡着逐渐收敛，但是有时候就会一直震荡。

我们接下来分别具体讲怎么改造两个限制条件的。
我们分别称其为：
divergence-free solver
constant density solver

divergence free solver

我们的目的就是保证
$$\nabla \cdot v=0$$

无散度条件还有另外一种形式 $$D\rho /Dt=0$$ 这个形式和上面的形式完全等价，不信你看：
$$D\rho /Dt=\partial \rho /\partial t+\rho \nabla \cdot v=0$$
这是对密度的全导数（或者叫物质导数material derivitive）。第一项是密度随时间的变化。第二项是由于流动所造成的密度变化，也称之为对流导数（convective derivative），或者叫平流导数(advective derivative)。
where $$\partial \rho /\partial t=0$$ 是因为密度不变。 于是两边再除以rho，即得到了第一个方程。
证毕。

我们的目的就是消除这个误差。让它在迭代中接近0。

怎么让它接近0呢？我们想到，流体粒子之所以不会过密的原因是：一旦过近，他们就会产生排斥力。这个力正是保证不可压缩性的根源。而这个力，正是压力梯度力。

所以思路是：只要我们找到正确的压力梯度力，让粒子的疏密程度恰好满足无散度条件就好了。

单位体积的压力梯度力正是
$$f_i^p=-\nabla p_i$$
为什么会有负号呢？因为粒子从压力高的地方被推向压力低的地方。

从而我们只要找到正确的
$$\nabla p_i$$
就可以了。

那去哪找呢？理想气体状态方程给了我们思路。我们知道，对一个物体施加的压力越大，密度越大。因为它被挤压了嘛！但是这个关系显然不是简单的线性关系。（WCSPH把它简化为线性关系，所以简单却又有问题）

虽然不是线性关系，但是我们在计算机中，早晚要转化为线性关系。不如引入暂且把它当成线性的，后面可以动态变化！这样即使不是线性的关系，也能有个简单好用的方案。这就比用一个常数得到了极大的进步。

后面是推导过程。我们这里先不讲。有空再说。我们直接给出结论。

我们的目的是建立如下类似线性的关系
$$\nabla p_i={\kappa }_i^v\nabla {\rho }_i$$
一定要记住其中的kappa是动态的！不是一个常数！

我们暂且称kappa为stiffness parameter。我们这里直接给出结论，跳过推导过程：

$${\kappa }_i^v=(1/\Delta t)(D{\rho }_i/Dt){\alpha }_i$$
$${\alpha }_i=\frac{{\rho }_i}{|{\sum }_j{m}_j\nabla W_{ij}{|}^2+{\sum }_j|m_j\nabla W_{ij}{|}^2}$$

注意到alpha分母两项的唯一区别在于：先求和再平方vs.先平方再求和

我们把kappa带回压力梯度那个公式。就得到了正确的压力梯度力。

值得注意的是，因为压力梯度力是对称力，即粒子i施加给粒子j之后，粒子j也应该等值反向地施加回粒子i。这就是牛顿第三定律。这就要用对称形式的SPH离散公式。

于是粒子i所受的压力梯度力就应该等于
$$f_i^p=-m_i\sum _j{m}_j(\frac{{\kappa }_i^v}{{\rho }_i}+\frac{{\kappa }_j^v}{{\rho }_j})\nabla W_{ij}$$

加速度就是力除以质量，所以下一时刻的速度应该更新为：
$$v_i:=v_i-\Delta t{f}_i^p/m_i$$

这个kappa不可能一次就是正确的，为此我们要用一个迭代循环把他保住，直到速度散度很小

算法流程就总结为如下表格

constant density solver

这一部分与上面类似。

我们的目标是
$${\rho }_i^{\ast }-{\rho }_0=0$$
其中rho0是静止密度，也就是物理上真实的密度。而rho*只是计算过程中的一个计算值而已。我们要让计算出来的密度尽量接近静止密度rho0。

我们的思路是：找到正确的压力梯度力，使密度接近静止密度。

那么同样是改造压力梯度力，让它乘以一个动态的系数后，得到密度。

我们同样跳过推导过程，直接给出结论。

$${\kappa }_i=\frac{1}{\Delta t^2}({\rho }_i^{\ast }-{\rho }_0){\alpha }_i$$

关键就在于：这个alpha和上面的alpha是一样的！所以我们可以重用以节约大量计算量。这正是DFSPH速度快的核心原因之一。

下面带回压力梯度力的公式是完全一致的，这里就不写了。直接写出算法流程。

值得一提的是，第4步是预测一个密度rho*，这个rho*就是迭代跳出的条件。
它的公式如下

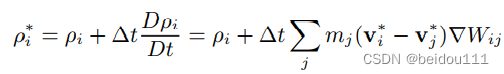
整个算法流程

DFSPH整个算法流程和其他的压力求解器没有太大的区别。

可以粗略地分为几大步：

1. 邻域搜索
2. 计算密度
3. 计算非压力梯度力
4. 更新无压力驱动的速度位置
5. 计算alpha
6. constant density solver
7. divergence-free solver
8. 更新有压力驱动的速度位置

如果采用自适应时间步长，可以加到第4步以后