前言
本文为GAMES101现代计算机图形学入门 的学习笔记系列。
我们的系列笔记将分为两部分:
- 课堂笔记
- 作业
原课程为2020年2月闫令琪所教授的 GAMES101 现代计算机图形学入门。
课程主页:https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html
(幻灯片和课程录像均在此处)
课程共计22节。作业共计8次。
针对人群:计算机图形学入门新手
教材:
Steve Marschner and Peter Shirley的"Fundamentals of Computer Graphics"
第三版或更新版本。目前无官方中文版。
民间翻译:https://www.stubbornhuang.com/1812/
2022-6-4
正文
本节课内容
- 2D变换:旋转、缩放和剪切
- 齐次坐标系
- 复合变换
- 3D变换
变换是干什么的?有两种
- 模型变换:模型本身变形
- 视角变换:相机或视角变化 或者 3D到2D的投影
2D变换
缩放

反射
例如对y轴反射。则x坐标取相反数,y坐标不变
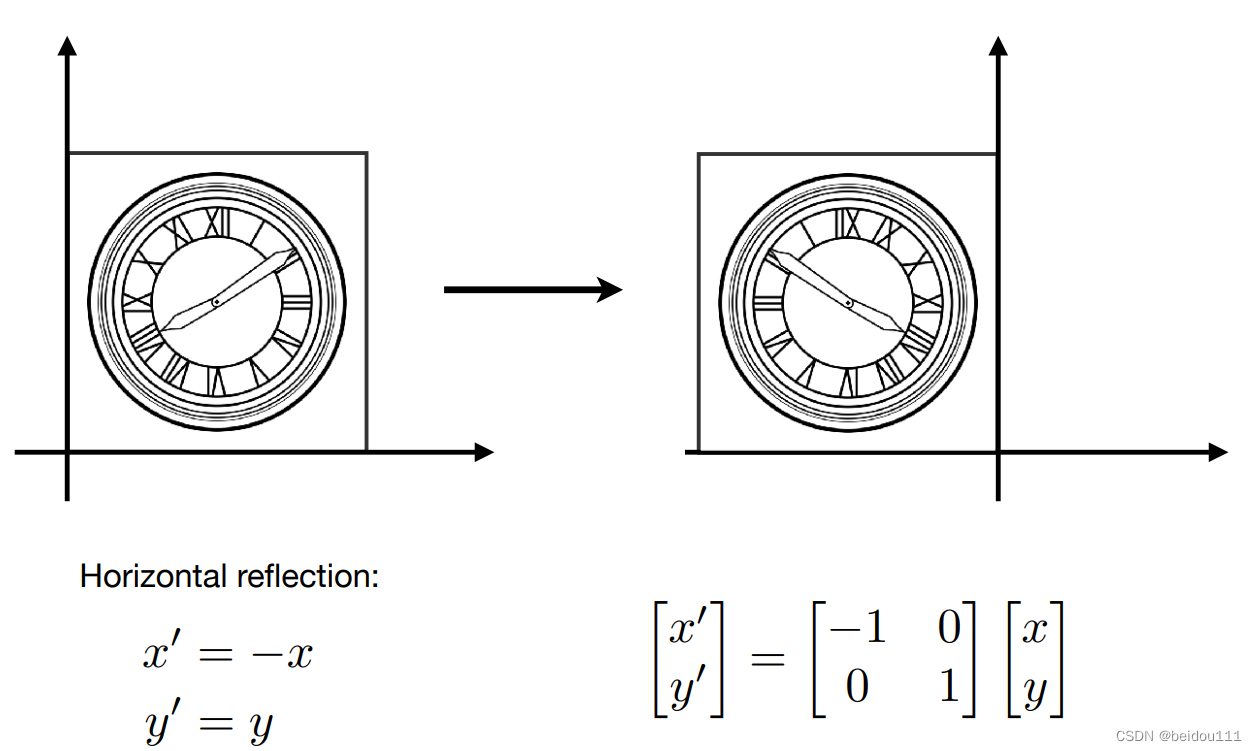
剪切
x坐标变化,y坐标不变
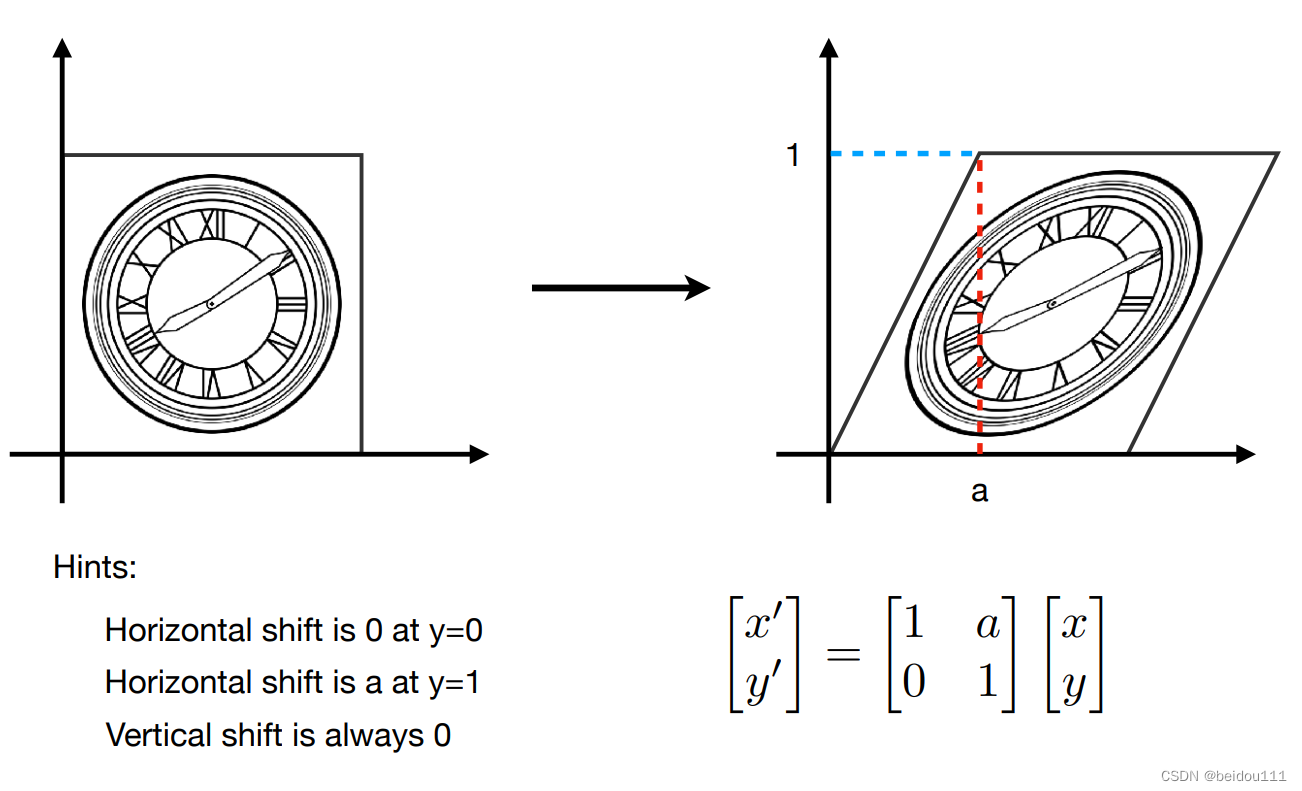
因为y坐标不变,所以矩阵的 第二行一定是[0 1]
再看x坐标: 在x轴上(y=0),不变 在最上边(y=1),向右平移a,即+a 所以在这两者之间: +ay
原本的坐标是x,故变换后x坐标为x+ay 故第一行为[1 a]
旋转
绕着原点逆时针转
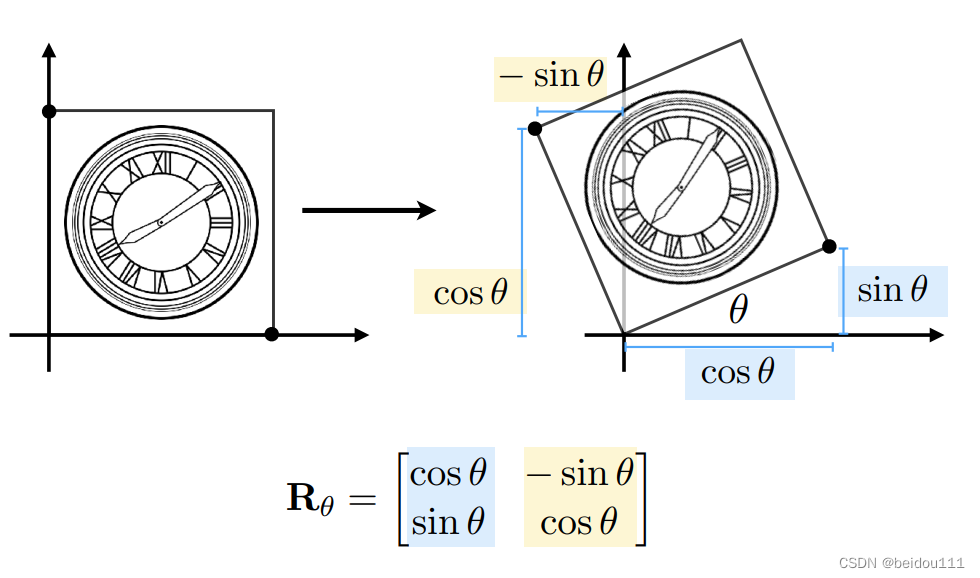
可以用待定系数法求矩阵R 首先将矩阵写为[A B; C D] 然后盯住一个点,例如右下角点 该点的原坐标为[1 0]
旋转后坐标为[ cos θ \cos\theta cosθ sin θ \sin \theta sinθ ]所以待定系数写出方程 ( A B C D ) ( 1 0 ) = ( cos θ sin θ ) \begin{pmatrix} A & B\\ C & D\\ \end{pmatrix} \begin{pmatrix} 1\\ 0\\ \end{pmatrix} = \begin{pmatrix} \cos\theta \\ \sin \theta \\ \end{pmatrix} (ACBD)(10)=(cosθsinθ)
就可以解出来 A= cos θ \cos\theta cosθ C= sin θ \sin\theta sinθ
同理,盯住左上角点,就可以解出来B 和D
线性变换
线性变换可以写成矩阵
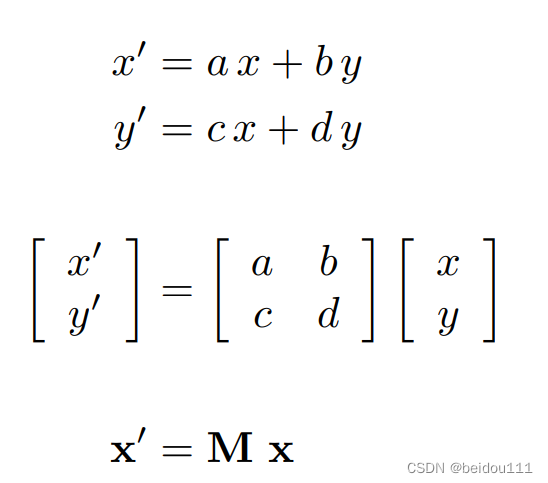
齐次坐标(仿射变换)
考虑到平移为
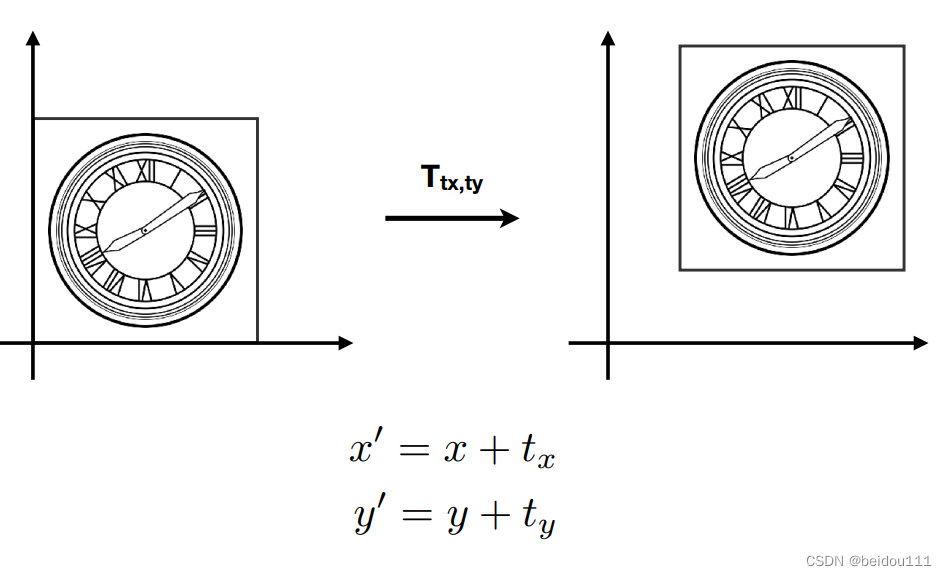

无法把平移融入到矩阵中去
于是升一维度
将二维的点和向量用三维坐标表示
点坐标补一个1,向量补一个0

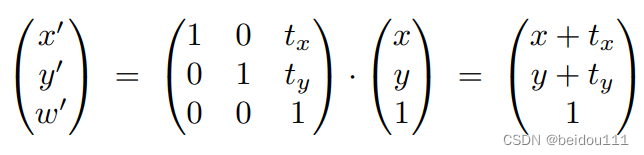
为什么要将向量与点的坐标区别对待呢?
因为向量要满足平移不变形,所以最后补充的是0
而点平移之后是变化的,所以最后补充的是1
同时,要满足以下操作:
- 向量+向量=向量 (结果最后一个坐标为0)
- 点-点=向量 (结果最后一个坐标为0)
- 点+向量=点 (结果最后一个坐标为1)
- 点 + 点 = 什么都不是(结果最后一个坐标为2)
故这是满足现实逻辑的。即
最后一个坐标是0则为向量,
最后一个坐标为1则为点,
最后一个坐标既不是1也不是0则什么也不是
但是为了不让最后一种违规情况出现,我们强行规定
假如最后一个坐标不是1,而是w,则所有坐标都除以w进行归一化
即
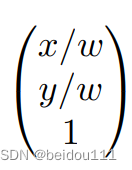
所以经过这种规定之后,我们把最后一种情况改为了
- 点 + 点 =两点的中点
(因为最后一个坐标为1+1=2,触发规定所有坐标同时除以2,所得坐标恰好就是中点)
我们将平移融入到矩阵之后,将该矩阵称之为仿射矩阵(affine matrix)
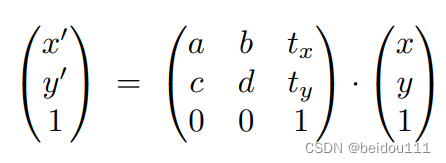
将之前的所有变换都总结到仿射变换里:

逆变换
变换矩阵的逆就是逆变换
例如将物体逆时针旋转45度的矩阵为M
则将物体顺时针旋转45度的矩阵为
M
−
1
M^{-1}
M−1
复合变换
变换矩阵相乘即可复合变换
- NOTE1 : 复合变换的顺序不可更改!
这是因为矩阵乘法不满足交换律
- NOTE 2: 要先从最右边的矩阵乘起
例如
T
R
(
x
y
1
)
TR\left(\begin{matrix} x\\ y\\ 1 \end{matrix}\right)
TR⎝
⎛xy1⎠
⎞
其中
(
x
y
1
)
\left(\begin{matrix} x\\ y\\ 1 \end{matrix}\right)
⎝
⎛xy1⎠
⎞是原坐标。所以当然要从离着原坐标最近的矩阵R乘起,然后再乘以T。因此总是从右向左乘。
- NOTE 3: 由于矩阵乘法满足结合律,所以可以提前算出来复合矩阵
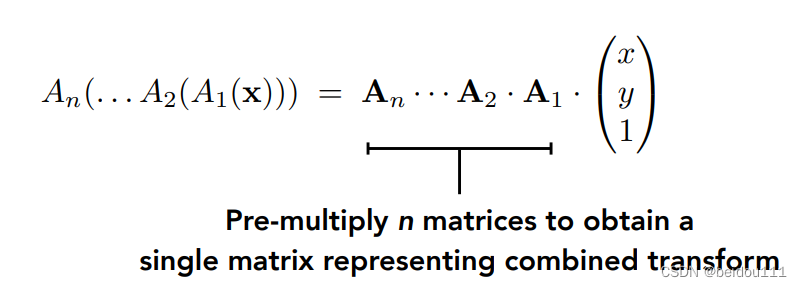
也就是图中的An…A1可以预计算为一个矩阵
而且其行数列数总是3x3
- NOTE4:绕着任意一点的旋转可以分解为先把这一点平移到远点,再旋转,然后再把该点平移回去
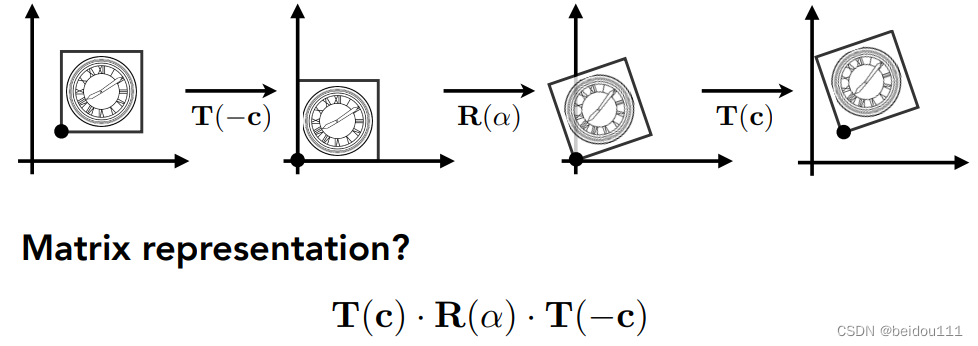
注意矩阵乘法对应变换是从右到左
3D变换
几乎与2D一致
齐次坐标
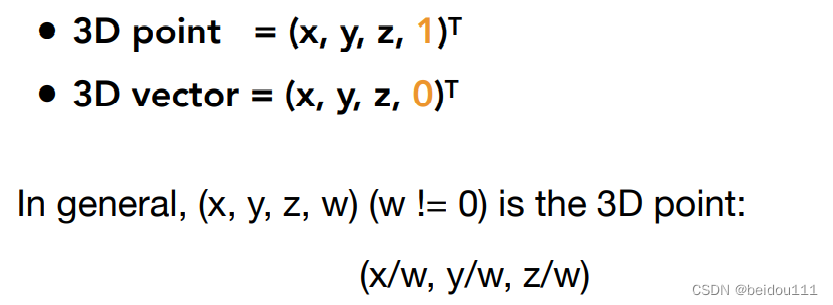
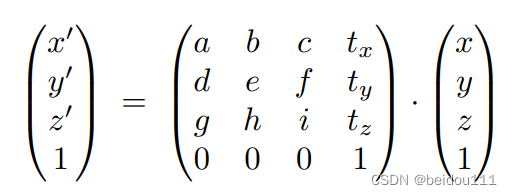





















 3572
3572











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








