2021-06-14

X门

让我们看一下我们的第一个量子逻辑门，即量子非门。毫无疑问，量子非门是经典非门的概括。在计算基础上，量子非门的作用与传统的非门类似，可以满足您的期望。也就是说，将∣0⟩状态变为∣1⟩，反之亦然：
NOT∣0⟩ = ∣1⟩
NOT∣1⟩ = ∣0⟩
但是，计算基础状态并不是量子位唯一可能的状态。当我们将NOT门应用于一般的叠加状态时，会发生什么情况，即α∣0⟩ + β∣1⟩？实际上，它几乎完成了最简单的事情：它线性地作用于量子态，互换了∣0⟩和∣1⟩的作用：
NOT（α∣0⟩ + β∣1⟩）= α∣1⟩ + β∣0⟩。
我一直在将NOT表示为量子NOT门。但是出于历史原因，从事量子计算的人们通常使用不同的符号X。因此，以上内容可能会被重写：
X（α∣0⟩ + β∣1⟩）= α∣1⟩ + β∣0⟩。
我将交替使用X门和NOT门这两个术语。
从历史上看，X符号的起源可追溯到1927年，当时物理学家Wolfgang Pauli提出了s_x运算(在当今的教科书中通常写为σ_x) 以帮助，描述某些对象，围绕x空间轴的旋转。此操作，后来引起从事量子计算工作的人们的兴趣。但是到那时，s（以及与旋转的关系）已经不相关了，所以s_x就正好成为X。
到目前为止，我们所看到的是，写下X门工作方式的代数方式。还有另一种表示形式，即量子电路表示形式。在量子电路中，我们将X门描述如下：

从左到右的线就是所谓的量子线。一个量子线代表一个量子比特。 “电线”一词及其绘制方式，看起来就像是量子位在太空中移动。但是，将左至右视为代表时间的流逝通常会很有帮助。因此，线的初始段只是时间的流逝，量子位没有任何反应。然后应用X门。然后量子线继续，留下所需的输出。 X门的第三个表示形式是值得一提的，表示形式为2 ×2矩阵：

H门

当然，X似乎并没有超越传统的NOT门所能做的所有事情。在本节中，我介绍一个明显涉及量子效应的门，即Hadamard门。
与X门一样，我们将首先说明Hadamard门如何在计算基础状态下起作用。用H表示门，这是它的作用：

当然，∣0⟩和∣1⟩不是唯一的量子态。Hadamard门如何作用于更一般的量子态？ 知道它像量子NOT门一样，线性起作用，这不会让您感到惊讶。特别是，Hadamard门将α∣0⟩ + β∣1⟩叠加到相应的输出叠加上：

这是Hadamard门的电路表示。看起来就像电路图中的X门，只是我们将门标签更改为H：

就像X门一样，H具有矩阵表示形式：

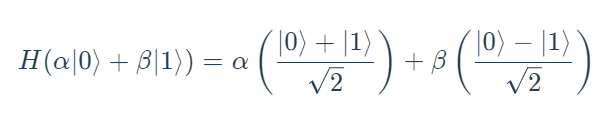
I门

I是2×2的单位矩阵

Y门

Y门与X门相似，但是它具有$i$和$-i$，而不是非对角线上的1，因此它需要 ∣0⟩到i∣1⟩和∣1⟩到−i∣0⟩：

Z门

Z门保持∣0⟩不变，并将∣1⟩变为−∣1⟩：

# CNOT门 这种门的一个示例是受控NOT（controlled-NOT或CNOT）门。在量子电路语言中，我们用两条线代表两个量子位，以下符号代表CNOT门：

上面带有填充小点的线（在本例中为顶部导线），称为控制量子位，其原因很快就会变得很清楚。带有较大的未填充圆的线，称为目标量子位。
到目前为止，我还没有说过两个量子位系统的可能状态，但是您可能会猜到。现在，我们有四个计算基础状态，对应于一个两位系统的四个可能状态：|00⟩，|01⟩，|10⟩和|11⟩。而且，对于一个二量子位系统，我们不仅可以拥有这四个状态，而且还可以具有它们的叠加（即线性组合）：
$\alpha \mid 00⟩+\beta \mid 01⟩+\gamma \mid 10⟩+\delta \mid 11⟩$
在这里，振幅α，β，γ，δ只是复数，并且绝对值的平方和为1，即$\mid \alpha {\mid }^2+\mid \beta {\mid }^2+\mid \gamma {\mid }^2+\mid \delta {\mid }^2=1$。这与我们对单个量子位使用的归一化条件相同。
现在，CNOT门很像量子NOT门，直接受经典门启发。它的作用非常简单。如果控制量子位设置为1，如在状态∣10⟩和∣11⟩中，则它将翻转（即NOT）目标量子位。否则它什么都不做。根据所有四个计算状态写出动作，我们有：

如果您熟悉经典的编程语言，则可以将CNOT视为一种非常简单的if-then语句：如果(if)设置了控制量子位，则(then)不是目标量子位。但是，虽然简单，但它可以用作构建其他更复杂的条件行为的基础。
有一种方法,可以将以上所有四个方程式汇总为一个方程式。假设x和y是经典位，即0或1。那么我们可以将上述方程式重写为一个方程式：$\mid x,y⟩\to \mid x,y\oplus x⟩$。
请注意插入逗号以使其更易于阅读–在处理多量子位状态时，这很常见。
上面的等式清楚地表明，CNOT会保留控制量子位x，但如果x设置为1，会翻转目标量子位y。请注意，⊕是加法模22，其中1⊕1= 0，正如我们从CNOT取∣11⟩到∣10⟩的事实所期望的那样。
CNOT就是这些。这真的是一个非常简单的想法和量子门。注意，正如我们对量子门所期望的那样，它当然在计算基态的叠加上，线性地起作用。所以：
$\alpha \mid 00⟩+\beta \mid 01⟩+\gamma \mid 10⟩+\delta \mid 11⟩\to \alpha \mid 00⟩+\beta \mid 01⟩+\gamma \mid 11⟩+\delta \mid 10⟩$
而且，尽管我不会明确进行验证，但CNOT是单式的，因此保留了我们所期望的量子态的长度。
当然，CNOT不仅会出现在两个量子位的计算中。它也出现在涉及更多量子位的计算中。假设我们有3个量子位，例如计算基础状态，如∣000⟩，∣001⟩等。这是一个CNOT，其中第二个量子位为控制量子位，第三个量子位为目标：

怎么回事？好吧，我们可以写出，在任意计算基础上的状态∣x，y，z⟩，其中x，y和z都是经典位。当然，第一位x根本没有改变，因为它不包含在CNOT中。第二位y是控制位，因此不会更改。但是如果控制位y设置为1，则第三位z被翻转。因此，我们可以将CNOT的动作写为：$\mid x,y,z⟩\to \mid x,y,z\oplus y⟩$

T门

Toffoli门与CNOT门非常相似，但是它没有单个控制量子位，而是具有两个控制量子位x和y，以及单个目标量子位zz。如果两个控制量子位都被设置，则目标被翻转。否则，目标将不予处理：