4.1 车辆动力学模型
注1:运动学模型和动力学模型最大的不同点在于
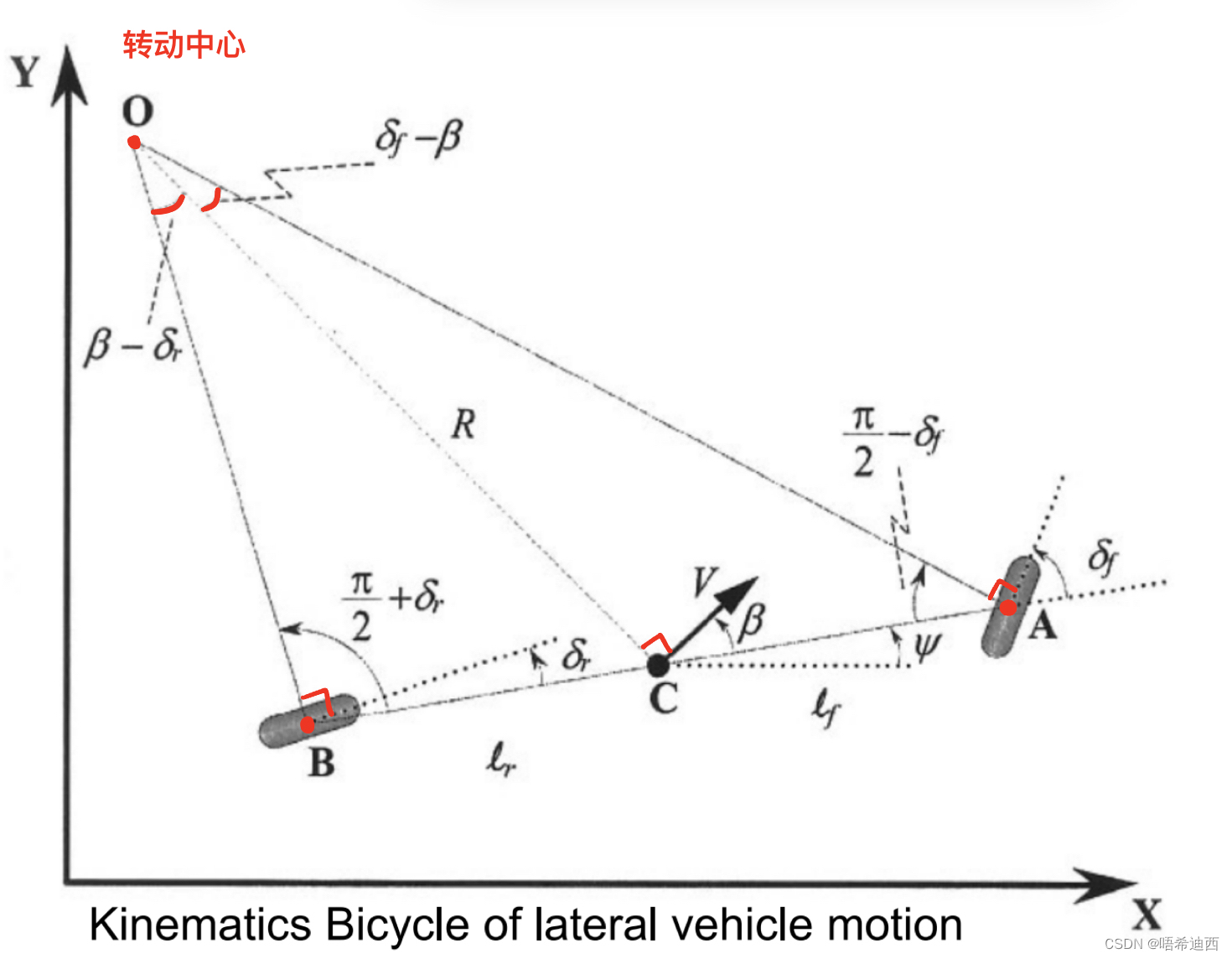
- 运动学模型是在我们不考虑车辆的受力情况下建立的(回顾我们推导出运动学模型的过程,我们没有使用到任何车辆所受的外力作为公式中的已知量,而是直接通过 “ 车速 + 横摆角 + 前后轮转角 ” 再辅以几何作图而得到的运动学模型);
- 动力学模型是在我们考虑了车辆在运动过程中所受外力(主要是轮胎侧向力)的情况下建立的;
a
注2:为何运动学模型可以不考虑外力对车辆的影响,而动力学模型必须考虑呢?
- 运动学模型的构建有一个很重要的前提,就是车辆是在 “ 低速 ” 状态下行驶的;而对于在低速状态下行驶的车辆,可以认为车辆和路面之间只有纵向的静摩擦,而没有侧向的动摩擦,即车辆与地面之间的侧向力很小,几乎可以忽略不记,因此不会造成轮胎的形变,进而可以认为轮胎朝向和轮胎速度方向是一致的;
- 动力学模型则是适用于高速行车条件,高速行车时车辆轮胎与地面之间不仅仅会有很大的纵向的滑动摩擦,还会有横向的滑动摩擦(高速行车但凡打一下方向盘,车轮胎就会因为变向而和地面产生巨大的横向滑动摩擦,导致轮胎强烈的形变),因此会导致轮胎速度方向和轮胎朝向并不相同,那么我们就要针对这种具有不可忽视的外力影响的行车情况再建立一个可以使用的模型,即车辆动力学模型;

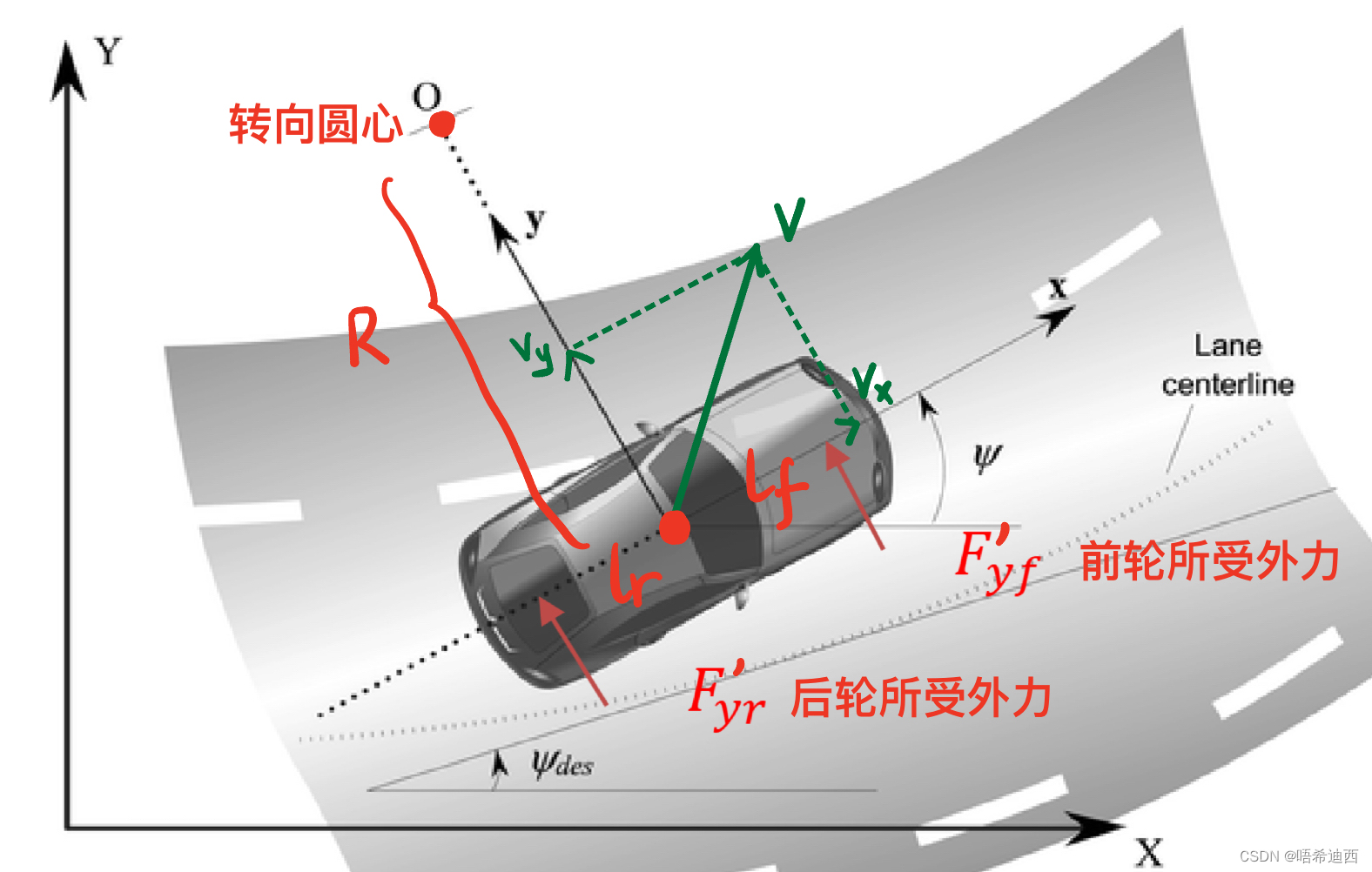
4.1.1 车辆的横向动力学模型
注:我们的目的是控制车辆沿着我们期望的轨迹行驶,保证行车轨迹路线满足车辆动力学特性;
前置假设:
- 车辆行车过程中转角比较小,这样可以保证车辆两前轮 / 两后轮的转角相差不大(由阿克曼几何推出),因此可以将两前轮 / 两后轮合并为一个轮胎来对待,这样我们就可以将车辆模型视为两轮自行车模型;
- 我们只考虑轮胎所受到的外力;而对于一些非线性的效应,如悬架结构 / 道路倾斜 / 空气动力学所造成的外力,我们选择忽略,虽然这些效应对于作用于轮胎的外力会有一定的影响,但是这样可以大大简化我们的建模任务;
- 忽略轮胎力的横纵向耦合关系;轮胎的横向力和纵向力是相互作用的,但是我们通常会假设轮胎力的横纵向是解耦过的(即互不影响,各自只影响各自方向上的运动),这样就可以将车辆的动力学模型分为横向动力学模型 + 纵向动力学模型,就可以更加简单清楚的描述车辆动力学特性;
a
a
注意:在本小节中推导横向动力学模型时,使用的是车身坐标系;但是车身坐标系无法真正意义上实现横纵向控制解耦,所以我们还需要把在车身坐标系中建立的横向动力学模型转换到自然坐标系中去,只有在 Frenet 才能真正实现横纵向控制解耦;
横向动力学模型推导过程:
注1:在车身坐标系中进行分析,车身坐标系是一个右手系;
注2:以车辆质心作为参考点(坐标系原点);
a
a
a
a
第1步:车辆的横向(侧向)动力学方程组
注:针对车辆整体进行受力分析,建立整车的横向动力学模型;
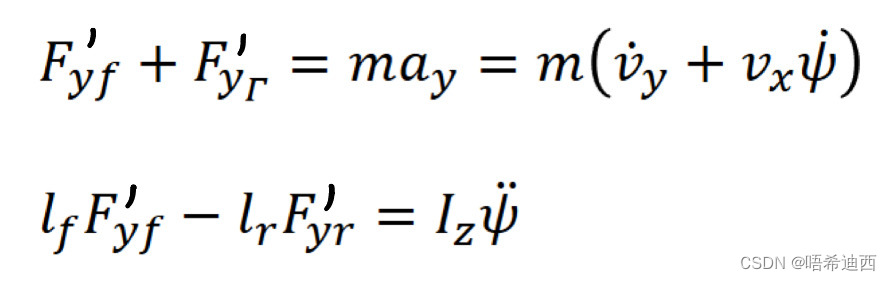
横向动力学方程组 注:我们可以发现,这个动力学模型是由两部分组成的,沿着y轴方向的平移运动,和沿着z轴方向的横摆运动;因此这个模型具有两个自由度,所以我们也称这个横向动力学模型是一个二自由度模型;
a
a
a
a
第2步:求出公式中的未知量
和
注1:接下来要完善横向动力学方程组,即将里面的未知量
和
消去,要计算这两个外力,就要针对轮胎的受力情况进行分析;这个时候我们就需要精细化的建模,不能再在整车上进行受力分析了,而是要从自行车模型上的前后轮胎上进行受力分析;
注2:在轮胎上力也分为纵向力和横向力;纵向力实现的是驱动和制动,而横向力则用来给车辆提供转向力并且保证行驶的稳定性;
注3:横向力一般是由于路面的侧向倾斜 / 侧向风 / 曲线行驶时产生的离心力而产生的;
注4:使用字母
代替角速度
(
并不代表任何半径,就是一个字母符号)
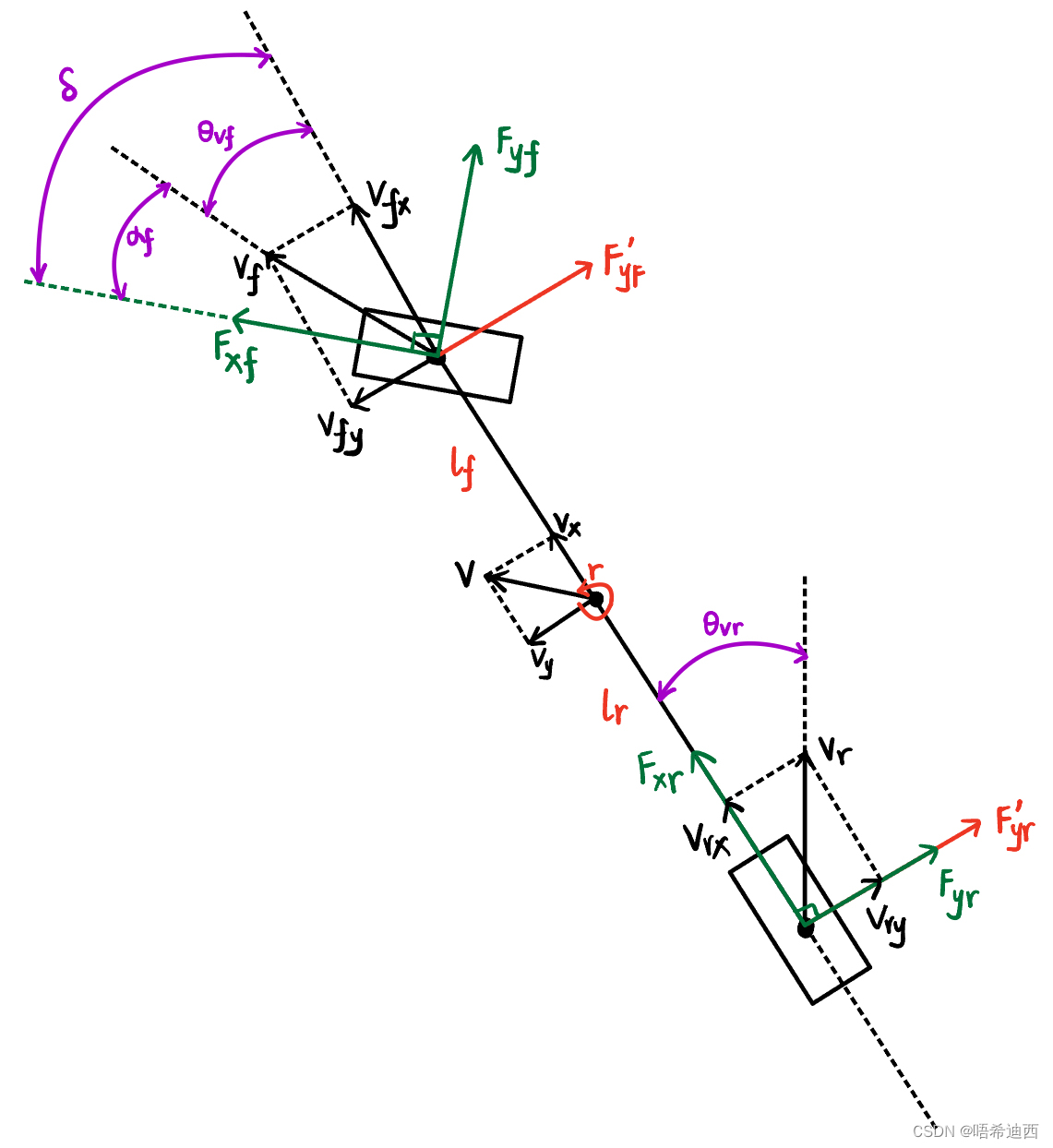
a
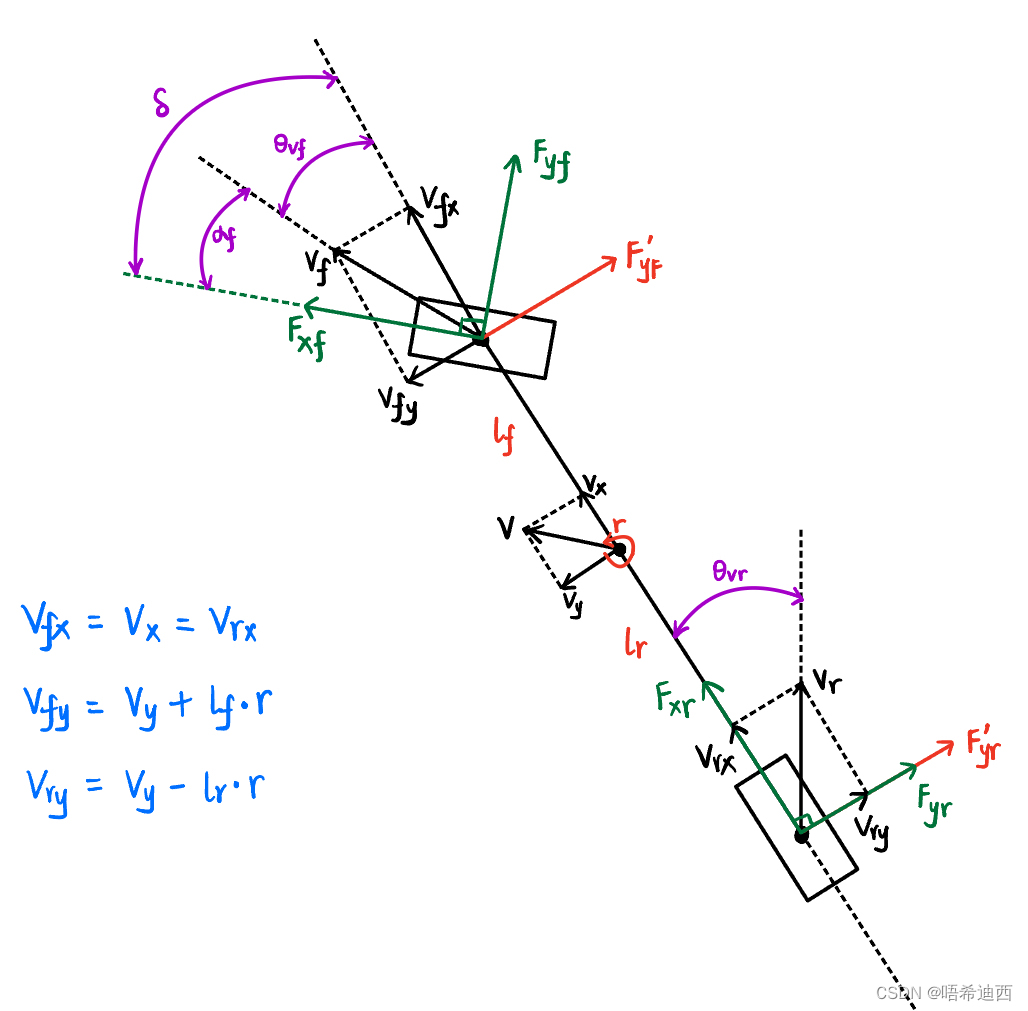
:前轮(朝向)转角(没有后轮转角,是因为认为后轮转角方向与车身纵轴方向一致,因为使用前轮控制转向而不是使用后轮,所以后轮转角为0)
:前轮速度转角(因为高速行车时轮胎速度和轮胎朝向之间有夹角,方向不一致)
:后轮速度转角
:前轮侧偏角
:前轮纵向力
:前轮横向力
:后轮纵向力
:后轮横向力
:车辆(质心)速度
:前轮速度
:后轮速度
即有横向动力学方程组表达式变为:
a
a
a
a
第3步:求出公式中的未知量
和
表达式
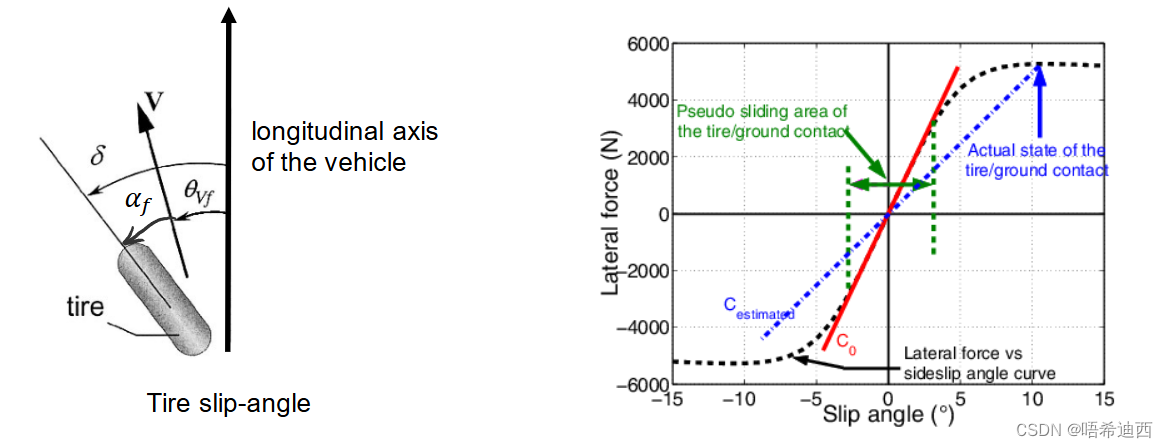
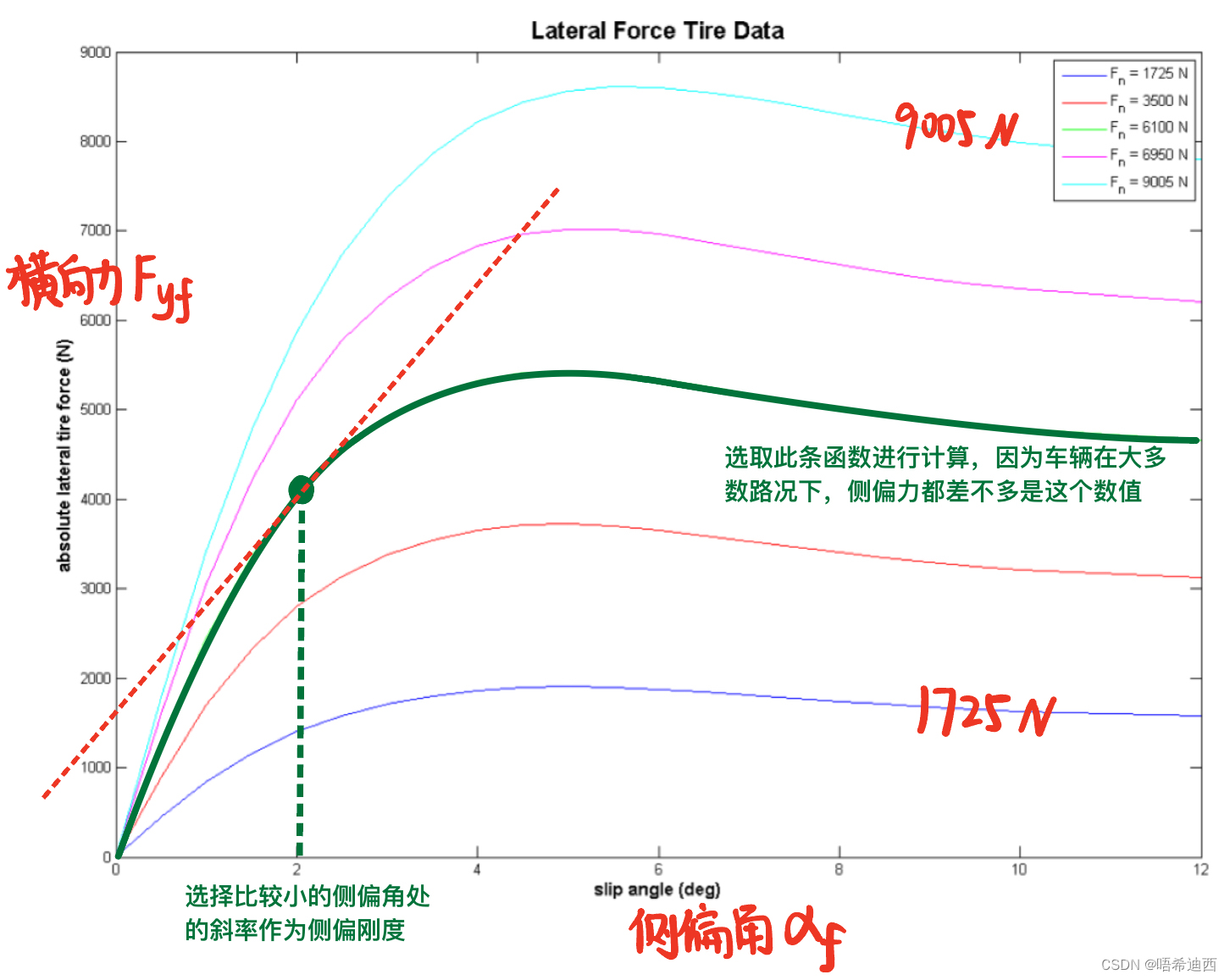
以前轮为例,要求施加在前轮上的横向力
的表达式,则通过上图(通过实验测出的,横轴为前轮侧偏角
,纵轴为前轮横向力
)可知,当前轮侧偏角很小的时候,前轮横向力
的大小与前轮侧偏角
之间的关系近似于正比例函数,而在车辆正常行驶的过程中车辆的前轮侧偏角是很小的,所以我们可以认为:
:前轮 / 后轮侧偏刚度(取图中轮胎侧偏角为0时曲线的斜率)
- 注意1:后轮转角(即后轮朝向角)与车辆纵轴方向相同,因此在车辆坐标系中
- 注意2:有其他的博客推导出的公式是乘上了2,是因为前轮 / 后轮都是两个,所以求的时候两个轮胎的受力都要算进去;但是我们的这个分析中的力
和
指的是两前轮 / 两后轮的侧向力的合力,所以不用乘2;
因此当前公式中的未知量为
和
;我们需要将他们表示出来;
a
a
a
a
第4步:求出公式中的未知量
和
表达式
注意1:这是在车身坐标系(右手系)下进行的分析;车辆朝向方向为x轴;
注意2:图中涉及到的速度都是标量(不带方向,即不带正负号,只有大小);
注意3:
,即
代表的是车辆的角速度;
a
a
a
a
a
第5步:将【
和
】的表达式代回【
和
】的表达式
a
a
a
a
第6步:将【
和
】的表达式代回【
和
】的表达式
注:
和
的表达式即为车辆的横向动力学方程组

该方程组即为横向动力学方程组 
代入后获得真正的横向动力学模型 a
a
a
a
第7步:化简横向动力学模型
a
(1)得到非线性横向动力学方程组:
a
(2)由于公式中包含了很多非线性的参数(三角函数部分),所以将公式中的三角函数部分进行化简,得到线性的横向动力学方程组:
注意:其中的未知量
会在这一步消去,所以在上面就根本不用求这个量的表达式;
a
(3)将横向动力学方程组转化为状态方程,选取状态
:
a
a
a
a
第8步:总结
注意:这样我们就在车身坐标系中建立起来了以【车辆横向速度
】和【车辆角速度(横摆角速度)
】为状态,以【前轮转向角
】为输入的线性横向动力学模型的状态空间方程描述;
a
a
a
a
补充:还可以选择其他的状态x,建立另一种形式的横向动力学模型
注意:基于全局坐标系
:车辆在Y轴上的坐标
:车辆横摆角(车辆航向)
4.1.2 横向动力学模型中一些参数的估算方法
关于质心位置的估算:(即估算
和
的值)
a
注:在车辆的四个轮子下面放四个秤,分别测量车辆在行驶过程中每个轮子上的压力值;
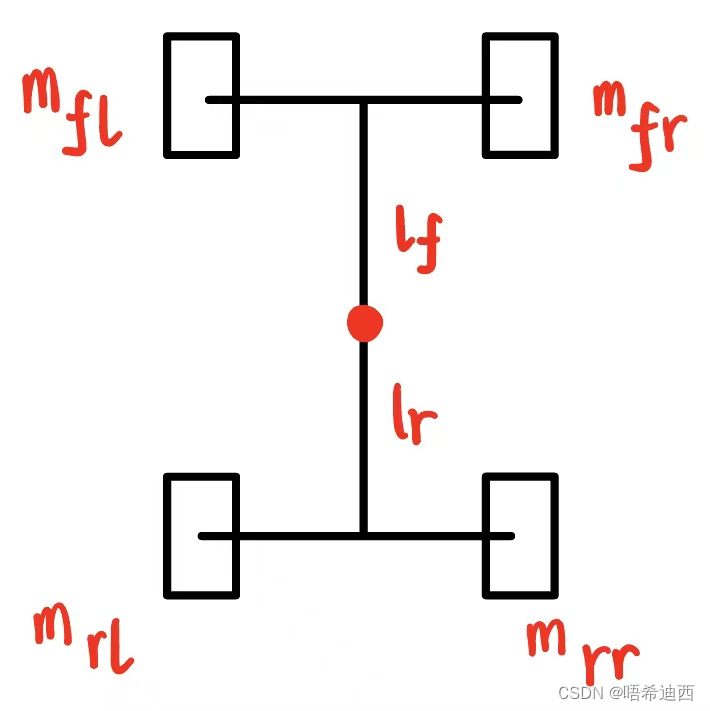
:左前轮压力
:右前轮压力
:前轮总压力
:左后轮压力
:右后轮压力
:后轮总压力
:车身总压力(总重量)
:纵向轴距
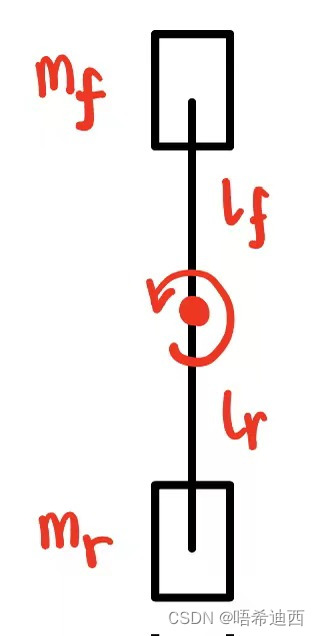
关于车辆的转动惯量
的估算:
a
关于侧偏刚度
和
的估算:
a
a
(1)如果可以直接从车厂拿到轮胎横向力
和轮胎侧偏角
的数据:
注:使用该侧偏刚度代表大多数行车情况下的侧偏刚度;
a
a
a
(2)如果无法从车厂拿到原始数据,则需要我们通过公式估算:
a
横向动力学模型:
a
将横向动力学模型修改为以侧偏刚度为变量的方程,这样通过方程中其他的已知量就可以通过解二元方程组求出侧偏刚度
和
:
a
但是实际上车辆上的传感器是无法直接测量到
和
的,只能直接测量到
和
,所以我们使用欧拉定理将连续的方程离散化,这样所有的量就都是已知的了:
- 比如转角
的值,本来这个是状态空间方程的输入,即是一个未知量,但是因为我们当前是在
时刻,所以
时刻的转角
其实是已知的,所以转化为离散型之后,方程中所有的量都是已知的了;
a
这样我们就把问题转化为了线性最小二乘法问题,我们可以通过做多组实验(实验条件应该符合一般的行车情况,这样求出的侧偏刚度才是最符合普通情况下行车的实际情况的)来得到一个线性方程组,通过最小二乘法求解:
a
a
a
a
a
a
a
4.2 线性二次调节器(LQR -- Linear Quadratic Regulator)
4.2.1 举例说明LQR控制器的设计思路 -- 1
当前的情况是:我们要选择一个代价最小的从起点到终点的出行方式,对于一个出行而言,选择不同的出行方式会花费不同的时间和不同的金钱;

对于不同的人,他们有的更看重花费少的时间付出更多的金钱,也有的人看重花费少的钱但是对时间的消耗无所谓;所以我们建立一个代价函数J,包含两个参数Q和R,分别代表时间在代价中占据的权重,和金钱在代价中占据的权重;
我们的目的是求出可以使得代价函数J的值尽可能小的出行方式是什么;

如果一个人认为时间更宝贵,想要花费更少的时间,而对金钱的花费没有要求,那么我们可以加大时间的权重Q,比如设置Q=30和R=1,这样我们求取使得代价值最小的解为直升机;

如果一个人认为金钱更宝贵,想要花费更少的金钱,而对时间的花费没有要求,那么我们可以加大金钱的权重R,比如设置Q=1和R=40,这样我们求取使得代价值最小的解为自行车;

对于普通人而言,如果能同时兼顾时间和金钱,使得时间和金钱都尽可能的少,那么可以选择Q=2和R=10,可以求得使得代价函数最小的解为公交车;

当我们取Q=1和R=5的时候,最优解同样还是公交车;因此可以得出结论,当Q和R矩阵保持一致的比例时,Q和R矩阵的取值对该问题的解没有任何影响;因此LQR控制器中重要的是Q和R矩阵之间的比值;

a
因此有代价函数J的设计理念:
- 使用Q和R矩阵作为权重,使用J作为代价;
- 矩阵Q和R各自的取值不重要,重要的是Q和R矩阵的比例关系;
4.2.2 举例说明LQR控制器的设计思路 -- 2
以车辆的横向控制为例:当车辆参考点和车辆当前位置不重合时,那么车辆具有一个横向误差;
车辆系统的线性状态空间方程组为:

- 假设状态空间方程的状态量 X 为 横向误差;
- 假设状态空间方程的输入量 U 为 方向盘转角;
a
a
a
任务背景:当系统的状态X出于某些原因偏离了平衡状态X=0的时候,我们能够在保证车辆平稳行驶的前提下(即尽可能不让方向盘转角变化的过于剧烈,同时也不要急转弯,方向盘转角就是控制器的输入U的变化程度),让系统的状态X尽可能快的回归到平衡状态;
设置代价函数J为二次型函数:令矩阵Q作为系统状态量X的权重,令矩阵R作为输入量U的权重;这样代价函数J就可以同时兼顾状态量X和输入量U的大小;

代价函数的设计理念:
- 关于作用:
- X代表系统状态,如果系统的状态偏离了平衡状态(指X=0),权重矩阵Q的取值越大,系统回归平衡状态的速度越快;
- U代表系统的输入,输入值是根据系统状态X所决定的(即 U = f (X) ),权重矩阵R的取值越大,系统调节的力度越小,系统状态量X到达平衡状态所需的时间越长;
- 关于函数的类型为二次型:
- 代价函数J中的被积分项为一个二次型函数,这是为了防止状态量X / 输入量U中存在负数,因此直接使用
和
来保证每个量都是正值(因为如果存在负值,那么积分的时候会存在消去的现象);
- 同时使用二次型函数作为被积分项还有一个优点,即二次型函数一定是凸函数,可以保证代价函数J一定存在极小值;
- 代价函数J中的被积分项为一个二次型函数,这是为了防止状态量X / 输入量U中存在负数,因此直接使用
- 关于矩阵Q和R的取值:
- Q与R矩阵均为人为给定的;
- 设计
和
;
- 即Q为半正定阵,R为正定阵;
- 一般为了方便,都是直接取R为单位阵,Q为对角阵,通过查看控制效果对应的修改Q矩阵的对角线元素;
- 且由于矩阵Q和R各自的取值不重要,重要的是Q和R矩阵的比例关系,所以可以直接取矩阵R为单位阵,人为调参Q矩阵即可;
- 每个对角元素
都是系统状态量X中某个分量
的权重值;

a
a
a
LQR控制器 + 车辆系统 的结构图:用LQR做控制器,关键就在于负反馈环节的设计(-K)
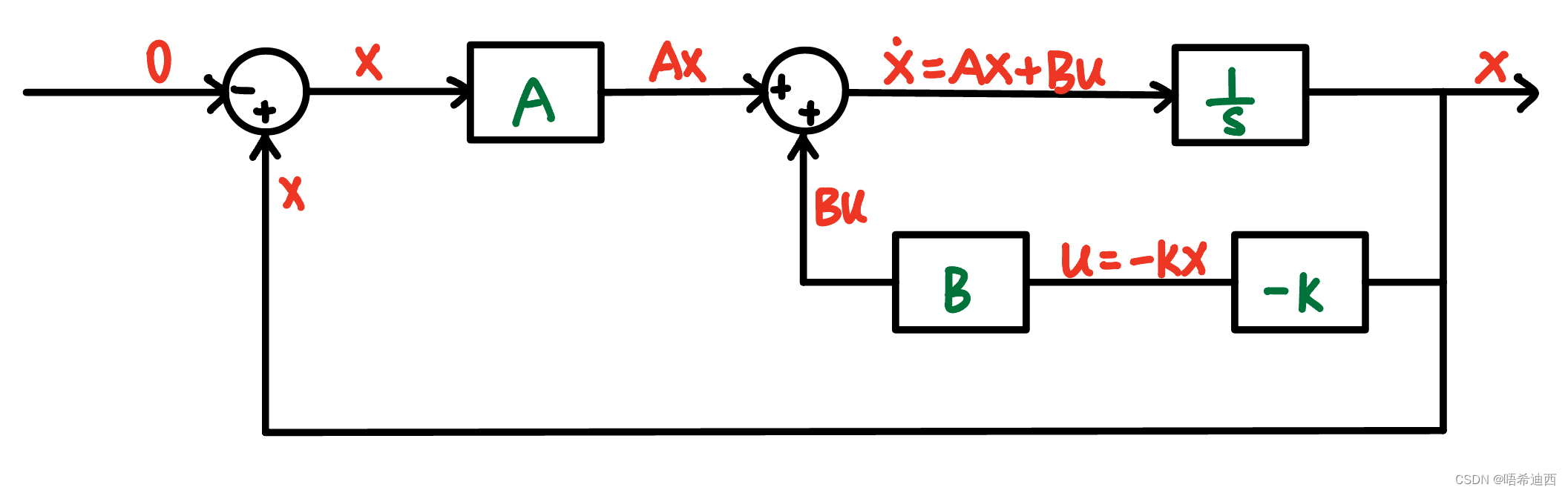
LQR控制器的设计理念1:LQR控制器控制的系统必须是一个【以误差作为状态量的系统】,这样才能保证状态量x的平衡状态为0,才能符合LQR的控制目标 -- 令系统收敛至0;
LQR控制器的设计理念2:LQR控制器通过使用来通过系统状态量得到系统输入量;指定控制器中的负反馈关系为U = -K * X的前提下,可否得到一个合适的矩阵K,使得
- 在U = -K * X时,代价函数J存在极小值;
- 在U = -K * X时,该系统的状态量X可以达到稳态(即该系统是收敛的);
已知内容:
- 矩阵A和B:通过系统的状态空间方程直接给定;
- 矩阵Q和R:人为调参调出来的,Q和R矩阵之间只有比例关系才会影响控制器的效果,所以可以直接给定矩阵R为单位阵,人为调参Q矩阵即可;
待求内容:
- 矩阵K的取值(U = -K * X)
a
a
a
因此有代价函数J的设计理念:
- 矩阵Q和R均为人为给定的;
- 矩阵Q为半正定,矩阵R为正定;
- 一般在实际应用时,将R设置为单位阵,将Q设置为对角阵,通过查看控制效果对应的修改Q矩阵的对角线元素;
- 由于矩阵Q和R的比例关系才会影响代价函数J的极小值点位置,所以可以直接给定矩阵R为单位阵,然后人为调参Q矩阵即可;
因此有LQR控制器的设计理念:
- LQR控制器所控制的系统状态量X的平衡状态为 X = 0;
- 所以系统一般都使用误差来作为状态量X,这样可以保证其稳态为0,与LQR控制器的控制目标契合;
- 总的来说:LQR所控制的系统必须是一个以误差作为状态量的系统;
- LQR控制器的输入U与系统状态X之间的关系固定为 U = -K * X;
- 我们的目的是得到一个LQR控制器中的取值合适的K矩阵,这个K矩阵必须使得当前系统能收敛,且代价函数J可以取得极小值;
4.2.3 举例说明LQR控制器的设计思路 -- 3
问题描述:一维系统中的LQR控制
- 有车辆系统的状态空间方程为:
(A与B矩阵均为一维的);
- 状态量X为横向误差,输入量U为方向盘转角;
- 系统的平衡状态为:
;
- 系统初始状态为:
;
目的:想使用LQR控制器控制车辆的横向运动,使得车辆可以在兼顾快速性(使状态量X快速收敛至平衡状态)和稳定性(LQR控制器输出的U不会有剧烈的波动)的前提下到达平衡状态;
a
a
求解LQR控制器:
1)设计代价函数:()

2)取:这就是LQR控制器指定的控制规律,矩阵K就是我们的待求量;
3)取:因为q与r的取值不重要,重要的是比例,所以直接指定
,调整q值即可;
4)推导K矩阵过程:
通过系统状态空间方程可得:

可知如果想让状态量最后收敛到0的话矩阵 K 要满足:
将 u = -K * x 代入代价函数 J:

将状态量 x 的表达式代入代价函数:
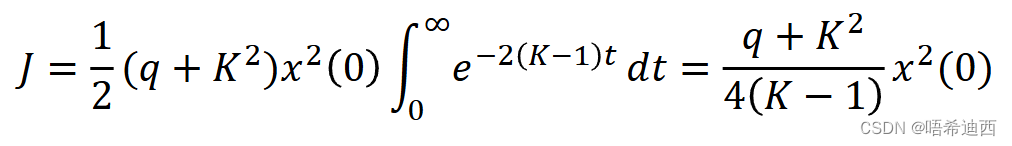
如果想让代价函数J存在极小值,要保证:

![]()
综上,矩阵K需要满足: &&
&&
因此K矩阵取值为:
5)LQR矩阵的核心控制原理为:
4.2.4 连续LQR控制器的详细推导
a
LQR控制器【最优控制策略】+【里卡提(Riccati)方程】的推导方法:
- 对于连续LQR控制器:
- 关于连续LQR控制器为什么选择使用 u = -K * x 作为最优控制策略,以及里卡提方程的推导过程,使用的方法涉及变分法和泛函分析;
- 详细推导:连续系统的LQR变分法推导 - 知乎
- 对于离散LQR控制器:
- 关于离散LQR控制器为什么选择使用 u = -K * x 作为最优控制策略,以及里卡提方程的推导过程,使用的方法仅涉及拉格朗日乘子法;
- 离散LQR对应的系统的状态空间方程也应该是离散的,因此还要将连续系统离散化;
- 详细推导:笔记92:连续状态空间方程转化为离散状态空间方程的详细推导 + 离散LQR控制器详细推导-CSDN博客
a
注:本小节主讲内容为连续LQR控制器的推到流程,这里仅使用一种不严格且易于理解的推导过程,来大致的讲述一下是如何推导出里卡提方程的,以及是如何计算出控制策略中的K矩阵的;因为如果在推导连续LQR时使用严格的推导过程,那将涉及很多超纲的知识,所以这里仅采用一种通俗易懂,但并不严格的推导流程,前后推导存在过渡生硬,无法解释为什么这样选择的地方,只需大致了解一下即可;
连续LQR控制器的推导流程:
a
a
a
总结:
- 里卡提方程:
- 最优控制策略:
a
连续LQR控制器的应用:
已知:
- 系统状态空间方程
;
- 代价函数
;
确定使用LQR作为控制器的前提下:
- 获得系统状态空间方程(要保证状态量x的平衡状态为0);
- 使用里卡提方程计算P矩阵;
- 使用P矩阵计算K矩阵;
- 获得最优控制策略 u = -K * x;
4.2.5 离散LQR控制器的推导
a
离散LQR控制器的应用:
已知:
a
a
关键公式:
- 离散状态空间方程:
- 里卡提方程:
- 最优控制策略:
a
a
确定使用离散LQR作为控制器的前提下:
- 获得系统状态空间方程(要保证状态量x的平衡状态为0);
- 使用里卡提方程计算P矩阵;
- 使用P矩阵计算K矩阵;
- 获得最优控制策略 u = -K * x;
a
a
注意:【离散状态空间方程】/【离散LQR的里卡提方程】/【离散LQR的最优控制策略】的计算在如下文章中进行了详细的推导
笔记92:连续状态空间方程转化为离散状态空间方程的详细推导 + 离散LQR控制器详细推导-CSDN博客
a
a
a
a
a
a
a
4.3 基于车辆横向动力学模型,使用LQR控制横向运动
注1:目前针对车辆纵向运动的控制,使用的都是【PID + 车辆运动学模型】
注2:目前针对车辆横向运动的控制,有两种方案
- 通过几何关系控制:【PID + 纯追踪法 / 斯坦利控制】
- 通过模型控制:【LQR + 车辆横向动力学模型】
4.3.1 车辆横向动力学模型的误差形式
在车身坐标系中建立起来的以【车辆横向速度】和【车辆角速度(横摆角速度)
】为状态量,以【前轮转向角
】为输入的【线性】横向动力学模型的状态空间方程描述:

注意:,即
代表的是车辆的角速度;
注:我们已经有了以
作为状态量的车辆横向动力学模型,但是这个模型并不能用LQR进行控制;因为LQR控制的系统必须保证其状态量的平衡状态为0,换言之LQR所控制的系统必须是以误差作为状态量的系统;但是当前这俩状态量的平衡状态不为0;所以如果想使用LQR控制器来控制车辆的横向运动,那么必须将当前这个车辆横向动力学模型修改为误差模型;
a
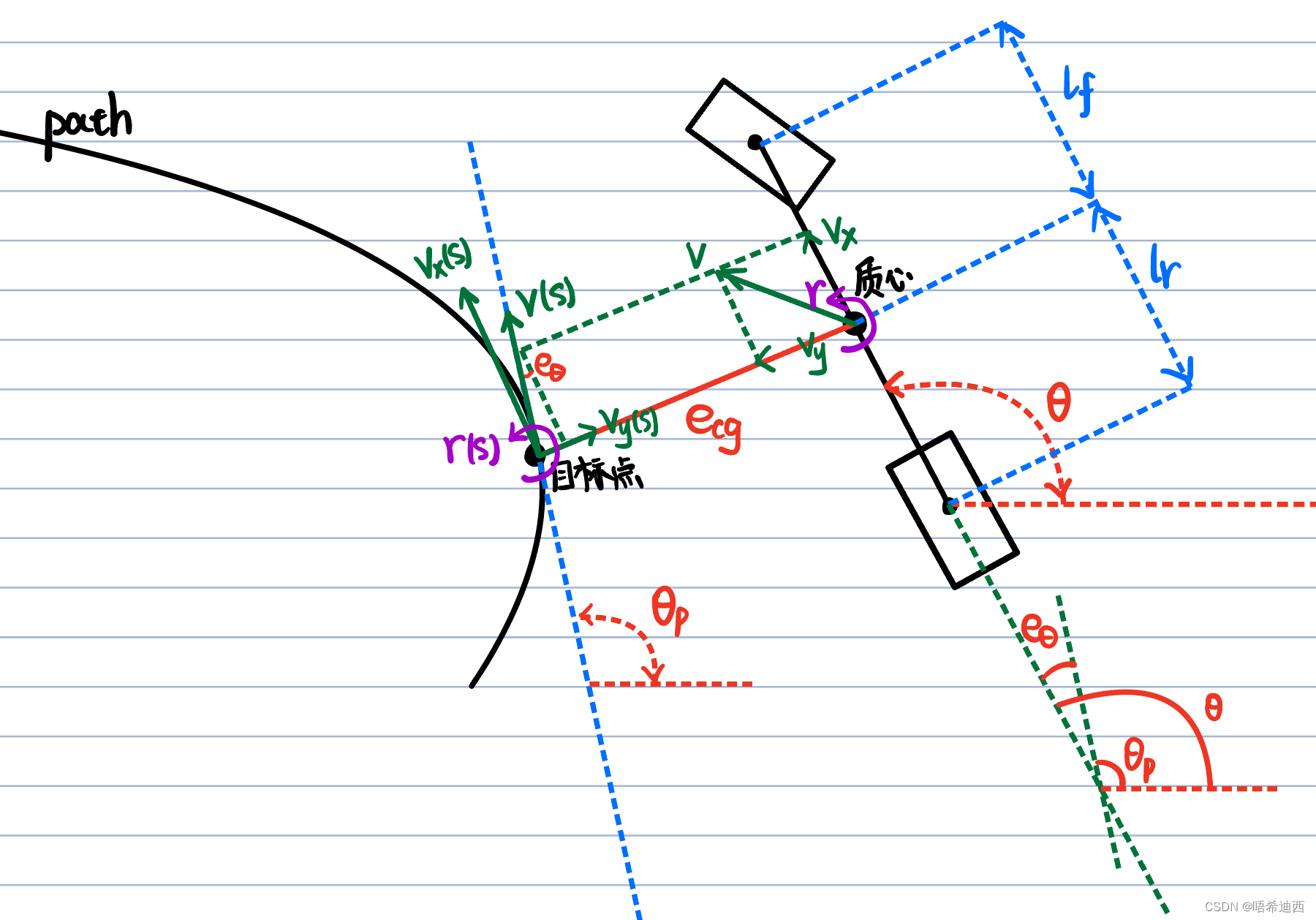
前导1:我们选择以下4个量作为系统状态量;
- 横向误差:
- 横向误差变化率:
- 航向误差:
- 航向误差变化率:
a
a
前导2:本节推导车辆横向动力学模型的误差表示形式的时候,需要3个假设;
- 车辆速度
的纵向分速度
是常数(即车辆一直使用同一个纵向速度前进);
- 目标点是规划路径中距离车辆质心最近的点,且这个目标点和车辆质心之间的连线垂直于车辆纵轴(这个假设只是为了便于分析,并无实际意义);
- 目标点的等效移动速度为
,以车辆坐标系为准,将
分解为分量
和
,并假定
;
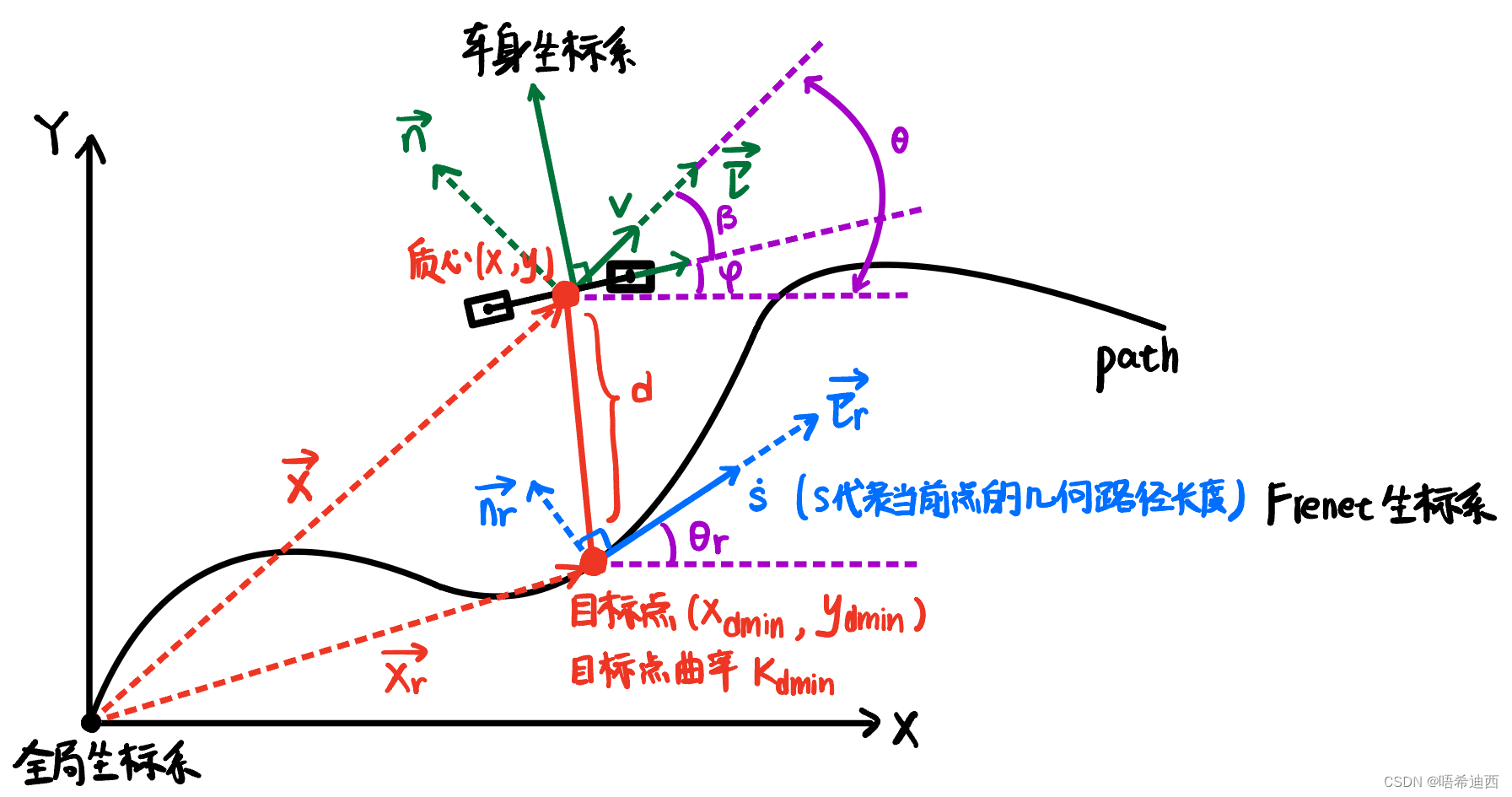
a
a
:车辆横摆角(即
,车辆的纵向车轴指向的方向,同时也是车辆的前进方向)
:目标航向角(即目标点处的切线与大地坐标系中X轴的夹角)
:航向误差
:横向误差
:车辆角速度
:目标点角速度
:目标点线速度
- 因为车辆在前进过程中,目标路径上和车辆质心当前位置匹配的目标点也是不断往前变化的,而目标点的变化既包含切向的线速度,也包含角速度;
- 将其角速度记为
;
- 将其线速度记为
,方向为目标点的切向;
注:与目标点相关的量全部带
;
a
a
注意:由于这三个假设的存在,所以本节的推导其实并不严谨,严谨的推导过程是没有这3个假设的,本节只是展示大致的推导过程,详细的推导过程请看下文;
a
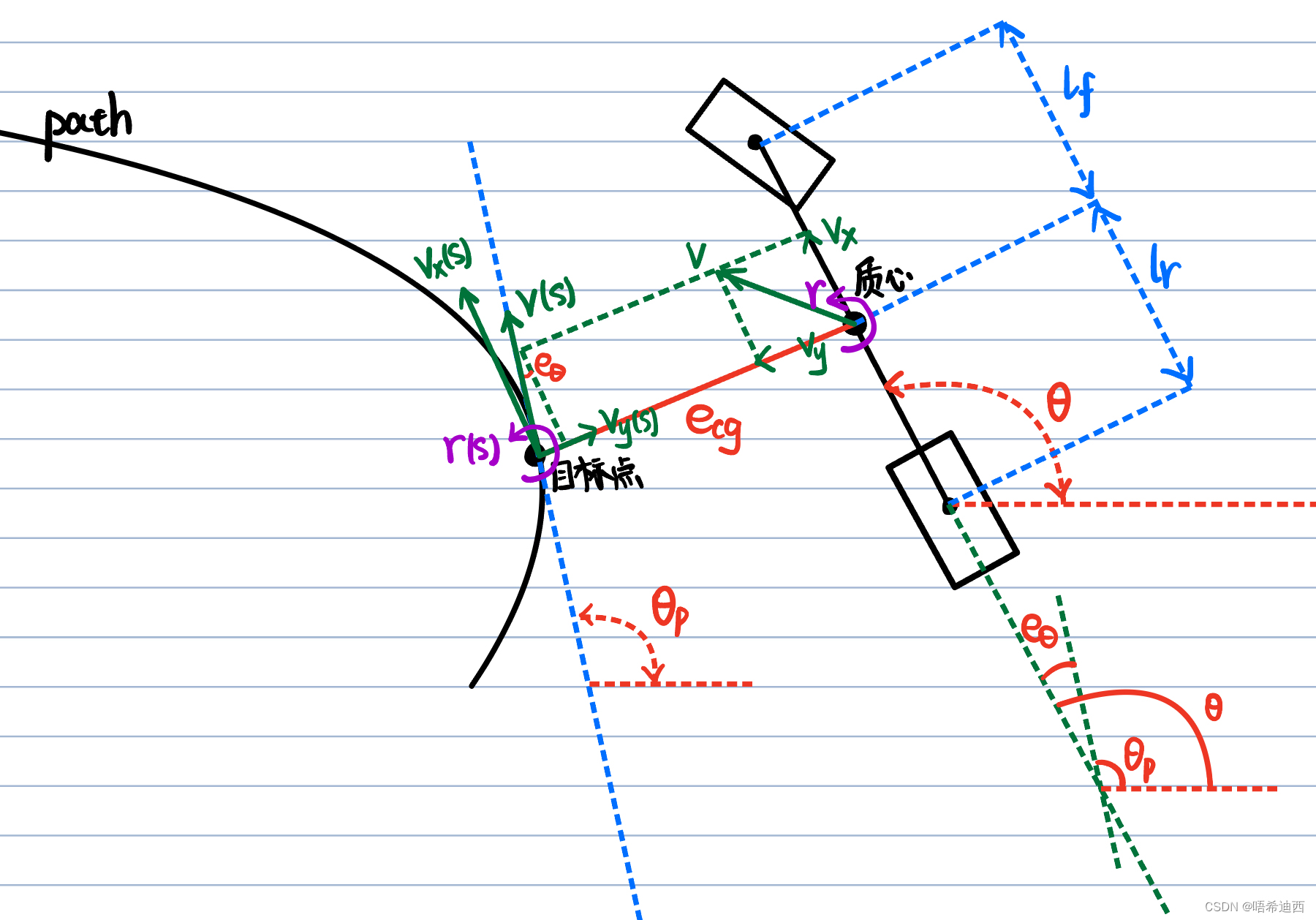
车辆横向动力学方程的误差形式 -- 推导过程:
因此:我们需要用上述4个新状态量(
,
,
,
)将原车辆横向动力学模型中的旧状态量(
,
)表示出来;
a
a
a
1)将
,
,
表示出来:

- 解释1:通过上图可知,车辆的角速度指向的是目标路径,因此车辆的角速度会导致
变大,即车辆的角速度
就是车辆朝向角
的变化率;
- 解释2:通过上图可知,车辆在前进过程中,和车辆当前质心位置匹配的目标点也是沿着
不断上移的,而目标点的移动会带来线速度和角速度,目标点的角速度
指向的是远离车辆的方向,因此目标点的角速度会使航向角
变大,而
即为航向角
的变化率;
- 解释3:
;
a
a
2)将
,
表示出来:

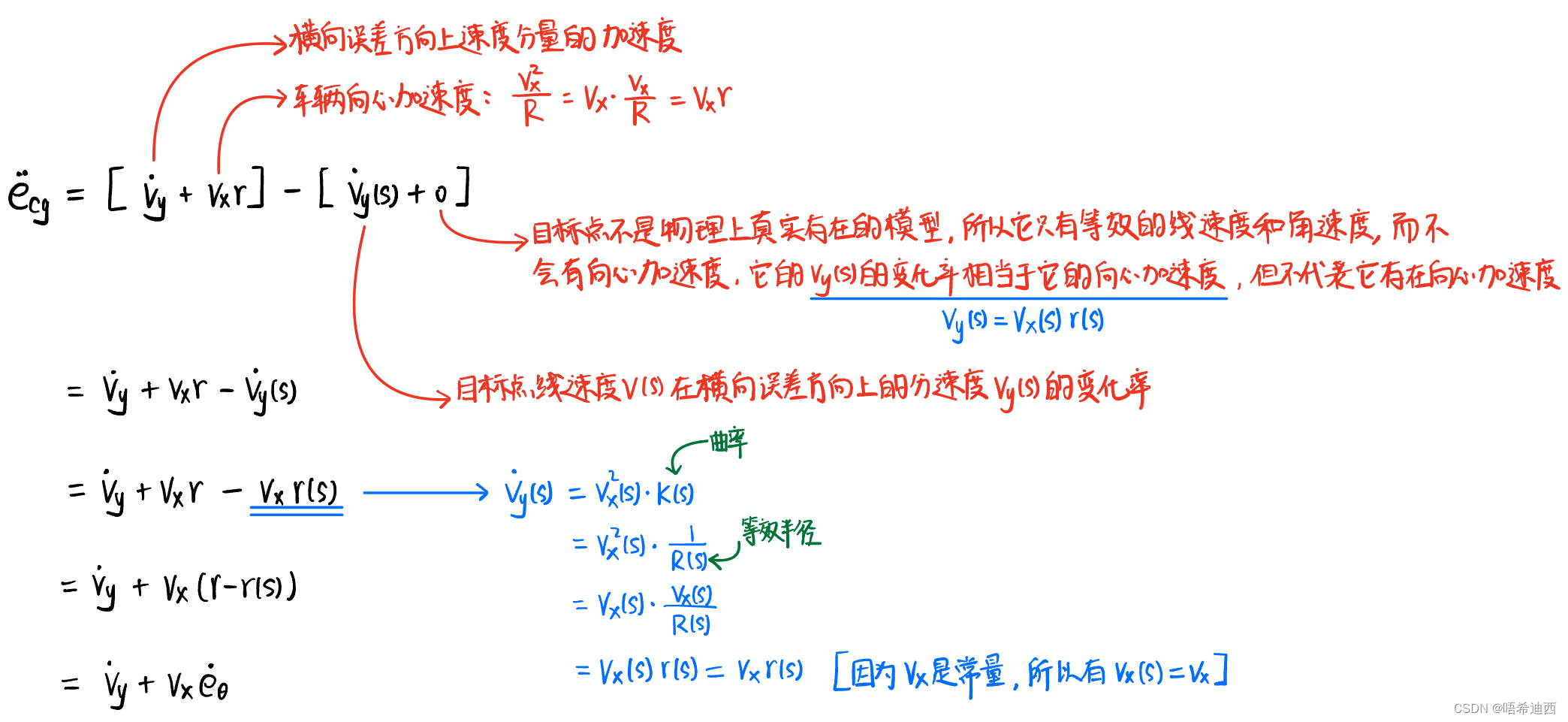
- 解释1:横向误差的变化率就是 -- 横向误差的大小
沿横向误差的方向(质心和目标点的连线)变化的速率;因此横向误差
的变化率包含两部分,一部分是车辆速度在该方向上的分速度,另一部分是目标点的移动导致的在该方向上的分速度;
- 解释2:车辆在该方向上的分速度是
;
- 解释3:目标点在该方向上的分速度是
;(因为车辆横向动力学模型建立的条件是高速 + 小转角情况,所以转角很小时,可视
)

- 解释1:
a
a
3)将公式代入原车辆横向误差模型的状态空间方程:
- 代换公式:
- 原车辆横向动力学模型:
- 代入过程:
a
a
4)得到误差型的车辆横向动力学模型的状态空间方程:
a
注意:上述推导为不严谨的推导,辅助我们理解得到误差型状态方程的过程罢了;下面的这篇文章则是不带任何假设的严谨且详细的推导流程;
笔记95:车辆横向动力学方程转化为误差形式 -- 详细推导过程-CSDN博客
4.3.2 使用DLQR,根据横向动力学模型,控制车辆的横向运动
Step0:我们在使用上述的状态空间方程的时候,只考虑矩阵A和B1,忽略矩阵B2;因为我们使用的LQR控制器只是针对状态空间方程的前两项(
)来确定控制作用的,第三项(
)并不受LQR控制;因此我们使用的状态空间方程为
;
a
a
Step1:验证误差形式横向动力学模型的能控性;
该矩阵行满秩,则该系统是能控的;
a
a
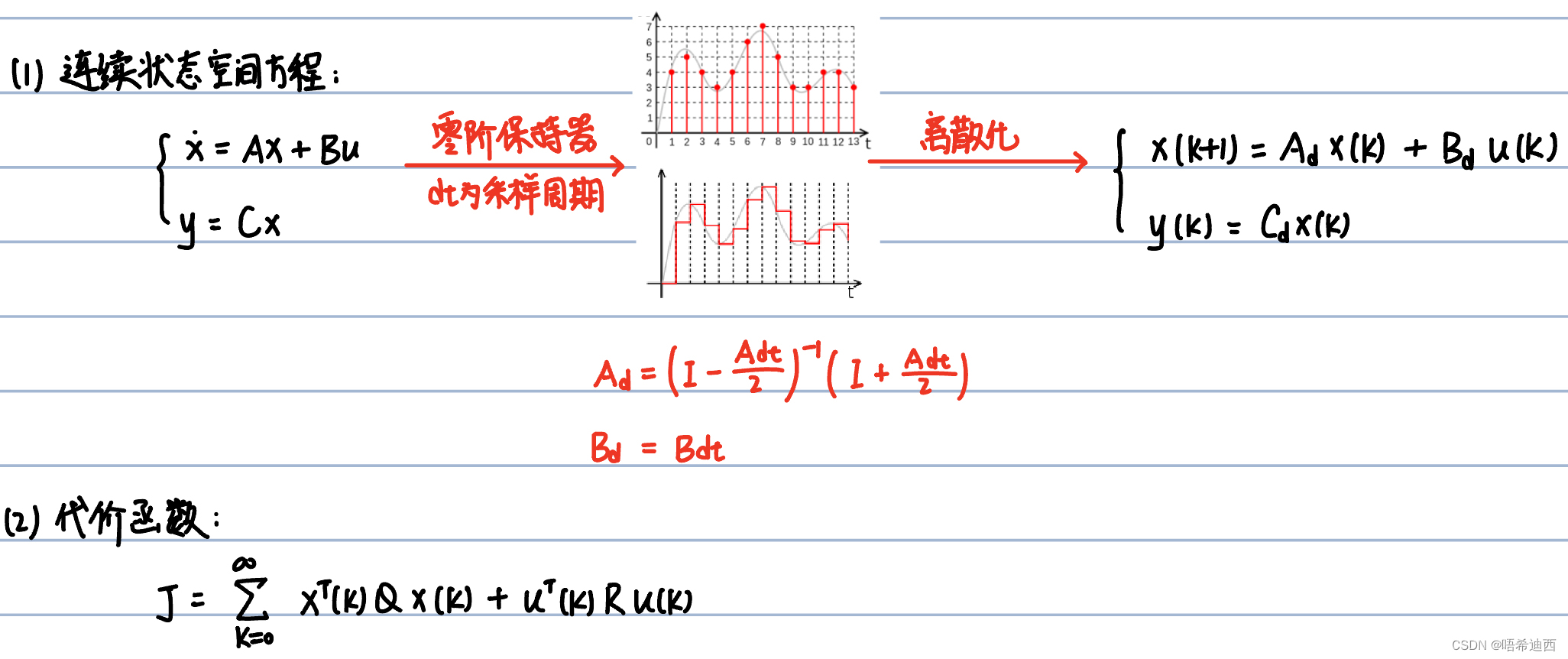
Step2:将连续状态空间方程化作离散型状态空间方程;
a
a
Step3:人为设定代价函数;取R阵为单位阵,取Q阵为对角阵;
用Q阵中对角线元素的取值确定状态量X中四个分量的重要性;
a
a
Step4:求解LQR控制器的控制策略
;
(1)里卡提方程求解P矩阵
(2)根据P矩阵求解K矩阵
(3)得到DLQR的控制策略
a
a
Step5:求解状态量X中包含的4个误差量;
(1)这里有个需要注意的地方:不用下面这4个公式计算误差量;因为这四个公式是粗略的推导,我们在实际编程的时候使用的是精确的推导式;

不精确推导式 (2)应该用下面这4个误差计算公式:
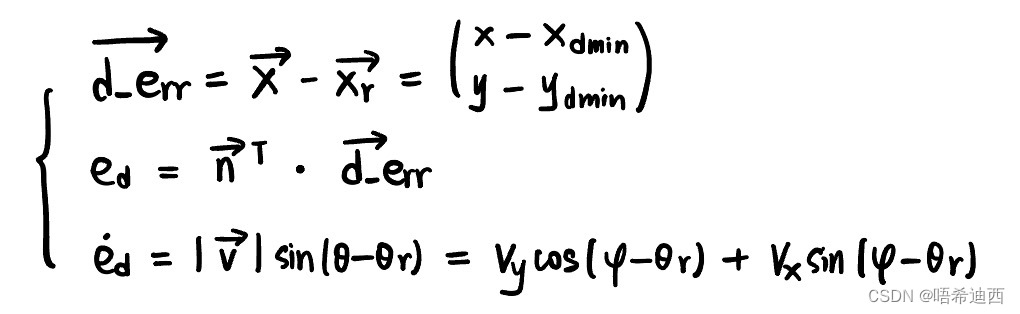
计算横向误差 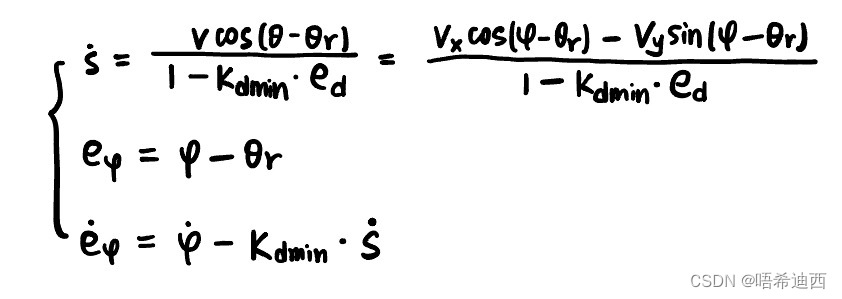
计算航向误差 a
a
Step6:已知系统状态量X和控制器矩阵K,即可得LQR控制器输出的对系统的控制命令
a
注意:针对误差型状态空间方程进行控制
- 使用反馈环节 -- 控制前两项 -- 原理为LQR
- 使用前馈环节 -- 控制第三项 -- 原理为:笔记96:前馈控制 + 航向误差-CSDN博客
4.3.3 LQR的弊端
弊端1:LQR的适用范围很小
注意1:LQR的全名可是线性二次调节器;
- 线性:指的是LQR只能针对线性系统进行调节;
- 二次型:指的是建立的代价函数是二次型函数;
注意2:正是因为LQR只对线性系统起作用,所以我们在对系统进行建模(建立状态空间方程)的时候,要对非线性系统进行线性化,这个特点就限制了LQR的应用范围;
注意3:而我们在建立车辆横向动力学模型的时候,是假设了【高速 + 小转角】的前提,正是因为这个小转角的假设,让我们可以将横向动力学模型中的非线性部分(三角函数部分)简化为纯角度;所以我们在使用LQR控制器的时候,就限制了使用范围必须为【小转角】的行驶场景,对于目标路径path的曲率很大的场景,使用LQR跟踪轨迹的效果会很差;
a
弊端2:LQR的跟踪缺少前瞻性(短视)
注意:LQR在跟踪目标轨迹时,目标点选择的是距离车辆当前质心最近的点,这就意味着LQR没有前瞻性,只将当前点作为跟踪对象,即只考虑了当前点的横向误差和航向误差;而没有考虑到未来的路径的变化;因此会导致目标路径出现较大的扰动(如:连续的S弯)时LQR的控制效果很差;
a
总结:
- LQR对于大曲率轨迹的跟踪效果不好,仅适用于小曲率轨迹的跟踪;
- LQR缺少前瞻性,对于多弯道型的道路跟踪效果很差;
a
a
a
a
a
a
a
4.4 基于多点预瞄的LQR控制器
注:该方法为针对LQR的改进,仅提出这种方法作为延伸拓展,有价值的是他的preview的思路;
原论文:https://www.cnki.com.cn/Article/CJFDTotal-QCJS201810003.htm
4.4.1 基于多点预瞄的LQR控制器
注:LQR控制在大曲率弯道处很难有好的控制效果,这是因为LQR控制只专注于当前目标点处的横向/航向误差,而对目标点后面的目标路径的变化毫不关心,因此当目标路径点处的曲率忽然变大,LQR时跟踪不上的;而如果可以让车辆还未进入急转弯道时(即匹配的目标点处还比较平滑时),就让车辆多打一点方向,这样就可以平滑的过渡进入急转弯,这样控制效果就好了;

解决方案:类似于MPC的思路,在当前匹配的目标点处,多往后看几个目标路径上的点,即存在一个固定长度的视窗,多收集一些未来信息;
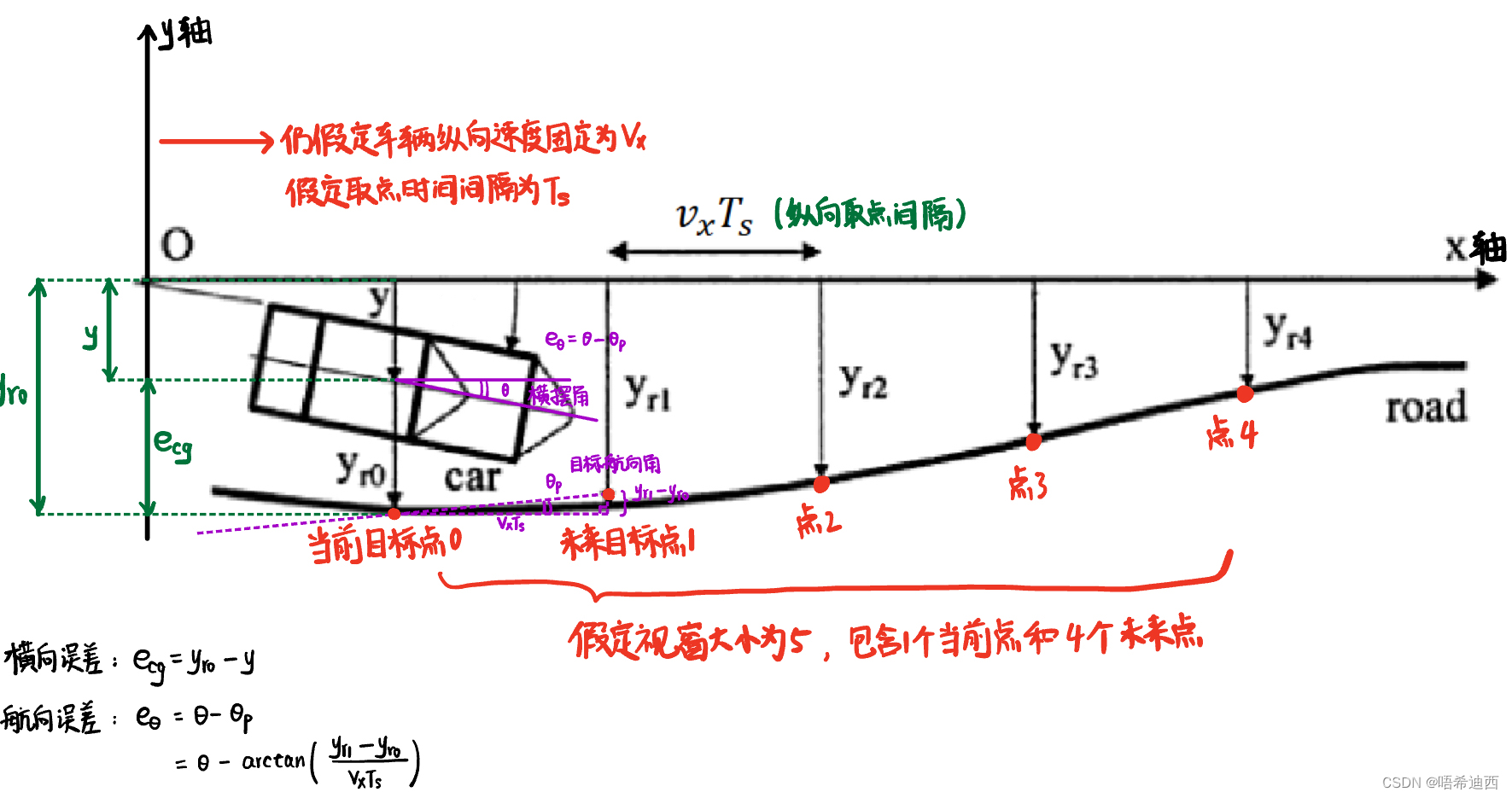
注:后面的推导过程中涉及的量均以该图为准;
a
a
Step1:
当车辆从当前目标点移动至下一目标点后,当前视窗也应同步变化,排除最旧的目标点,同时为了保证视窗长度一致,应再新加一个目标点进入;
a
a
Step2:
有车辆的原始横向动力学模型(连续):

注意:该模型是基于全局坐标系推导出来的
:车辆在Y轴上的坐标
:车辆横摆角(车辆航向)
有车辆的原始横向动力学模型(离散):
a
a
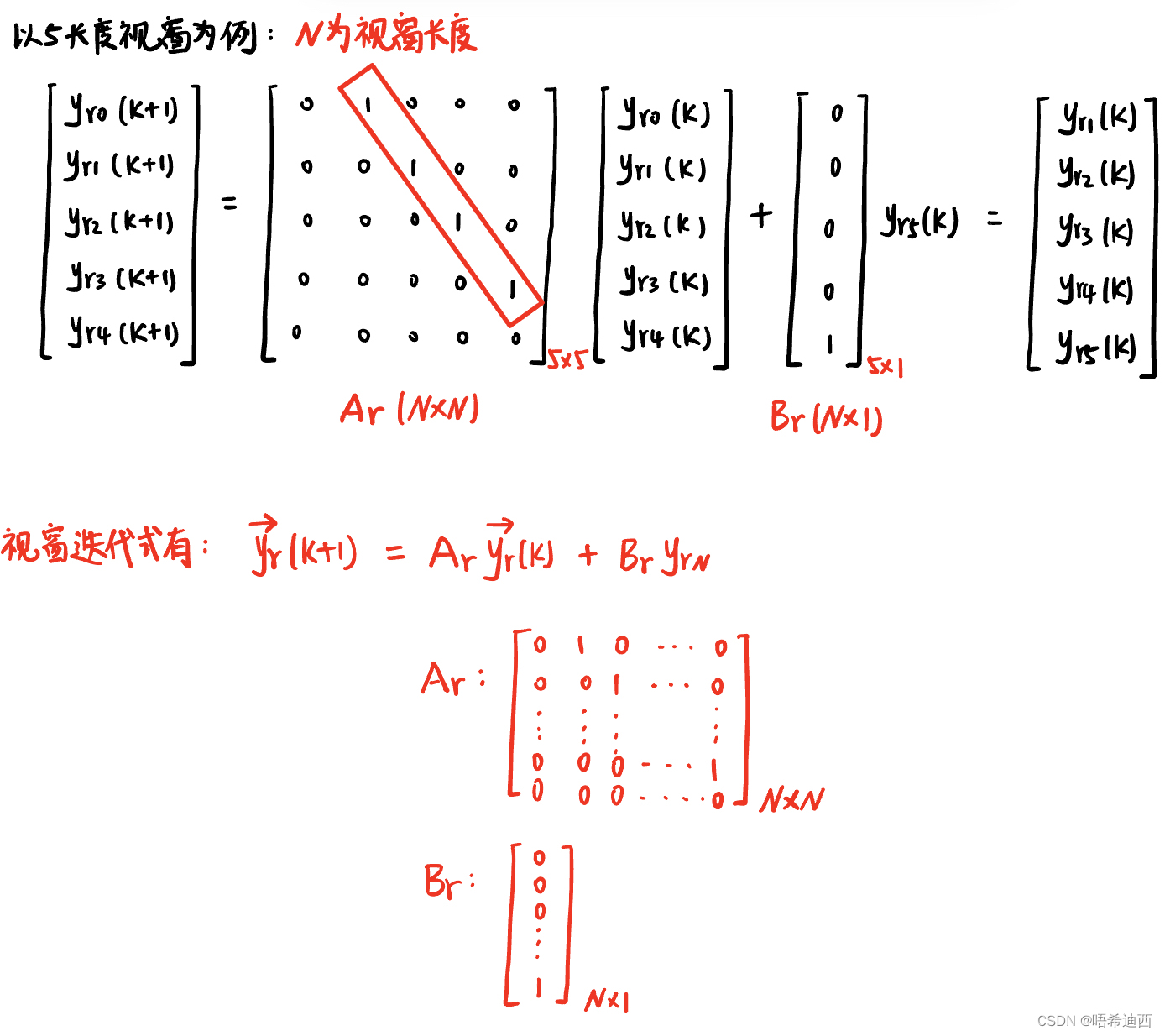
Step3:
联立【视窗迭代公式】+【原始车辆横向动力学方程】=【新状态空间方程】:
注意1:我们获得的这个新状态空间方程并不是误差形式的,不能直接使用LQR;
注意2:将前瞻信息加入了状态量X中,使得系统模型包含更多的未来信息;
a
a
Step4:
针对新系统(新状态空间方程)建立代价函数
,在代价函数中将系统表述为误差型:
a
a
Step5:
使用LQR求解:由于带上了前瞻内容,控制效果变好
a
a
a
a
a
a
a
4.5 代码实现
4.5.1 LQR控制器 -- 代码
头文件1:
#ifndef COMMON_H_
#define COMMON_H_
#include <fstream>
#include <iostream>
#include <string>
#include <nav_msgs/msg/odometry.hpp>
#include <std_msgs/msg/header.hpp>
#include <vector>
#include "map.h"
#include "reference_line.h"
#include "rclcpp/rclcpp.hpp"
#include <tf2/LinearMath/Quaternion.h>
#include <tf2/transform_datatypes.h>
#include <tf2_geometry_msgs/tf2_geometry_msgs.h>
#include <tf2/convert.h>
// 车辆状态信息
struct VehicleState {
double x; // 车辆在【全局坐标系】中的 -- x值
double y; // 车辆在【全局坐标系】中的 -- y值
double heading; // 车辆在【全局坐标系】中的 -- 车辆朝向(车辆横摆角/航向角)
double kappa; // 车辆在【全局坐标系】中的 -- 曲率(转弯半径的倒数)
double velocity; // 车辆在【全局坐标系】中的 -- 线速度
double angular_velocity; // 车辆在【全局坐标系】中的 -- 角速度(横摆角变化率)
double acceleration; // 车辆在【全局坐标系】中的 -- 加速度
double vx; // 速度在【车身坐标系的x轴】上的分量
double vy; // 速度在【车身坐标系的y轴】上的分量
double vz; // 速度在【车身坐标系的z轴】上的分量
// 规划起点
double planning_init_x;
double planning_init_y;
double roll;
double pitch;
double yaw;
double target_curv;
// added
double start_point_x;
double start_point_y;
double relative_x = 0;
double relative_y = 0;
double relative_distance = 0;
};
// 轨迹(目标)点
struct TrajectoryPoint {
double x; // 目标点在【全局坐标系】中的 -- x值
double y; // 目标点在【全局坐标系】中的 -- y值
double heading; // 目标点在【全局坐标系】中的 -- 目标点处的切线与全局坐标系的x轴之间的夹角(目标航向角)
double kappa; // 目标点在【全局坐标系】中的 -- 目标点处的曲率
double v; // 目标点在【全局坐标系】中变化的 -- 速度
double a; // 目标点在【全局坐标系】中变化的 -- 加速度
};
// 目标轨迹(vector容器中装有所有的路径点)
struct TrajectoryData {
std::vector<TrajectoryPoint> trajectory_points;
};
// 车辆横向动力学模型(误差型)中状态量x包含的4个分量
struct LateralControlError {
double lateral_error; // 横向误差
double heading_error; // 航向误差
double lateral_error_rate; // 横向误差变化率
double heading_error_rate; // 航向误差变化率
};
// 控制命令
struct ControlCmd {
double steer_target; //横向控制命令:方向盘转角
double acc; //总想控制命令:油门开度
};
struct EulerAngles {
double roll, pitch, yaw;
};
typedef std::shared_ptr<LateralControlError> LateralControlErrorPtr;
#endif头文件2:
#ifndef LQR_CONTROLLER_H_
#define LQR_CONTROLLER_H_
#pragma once
#include <math.h>
#include <fstream>
#include <iomanip>
#include <memory>
#include <string>
#include "Eigen/Core"
#include "common.h"
using Matrix = Eigen::MatrixXd;
class LqrController {
public:
LqrController();
~LqrController();
void LoadControlConf();
void Init();
bool ComputeControlCommand(const VehicleState &localization, const TrajectoryData &planning_published_trajectory, ControlCmd &cmd);
protected:
void UpdateState(const VehicleState &vehicle_state);
void UpdateMatrix(const VehicleState &vehicle_state);
double ComputeFeedForward(const VehicleState &localization, double ref_curvature);
void ComputeLateralErrors(const double x, const double y, const double theta, const double linear_v, const double angular_v, const double linear_a, LateralControlErrorPtr &lat_con_err);
TrajectoryPoint QueryNearestPointByPosition(const double x, const double y);
std::shared_ptr<TrajectoryData> QueryNearestPointByPositionWithPreview(const double x, const double y, const int preview_points_number);
void SolveLQRProblem(const Matrix &A, const Matrix &B, const Matrix &Q, const Matrix &R, const double tolerance, const uint max_num_iteration, Matrix *ptr_K);
std::vector<TrajectoryPoint> trajectory_points_; // 目标轨迹
double ts_ = 0.0; // 每隔ts_时间进行一次控制(LQR是定频控制车辆的)
double cf_ = 0.0; // 前轮侧偏刚度,左右轮之和
double cr_ = 0.0; // 后轮侧偏刚度,左右轮之和
double wheelbase_ = 0.0; // 车辆纵轴长度
double mass_ = 0.0; // 总车质量
double lf_ = 0.0; // 汽车前轮到中心点的距离
double lr_ = 0.0; // 汽车后轮到中心点的距离
double iz_ = 0.0; // 汽车的转动惯量
double steer_ratio_ = 0.0; // 方向盘的转角到轮胎转动角度之间的比值系数
double steer_single_direction_max_degree_ = 0.0; // 最大方向盘转角
// 关于【连续型】【误差型】【车辆横向动力学状态空间方程】:
const int basic_state_size_ = 4; // 状态空间方程中状态量x的维数
Eigen::MatrixXd matrix_a_; // 矩阵A
Eigen::MatrixXd matrix_a_coeff_; // 辅助计算矩阵A的矩阵
Eigen::MatrixXd matrix_b_; // 矩阵B
// 关于【离散型】【误差型】【车辆横向动力学状态空间方程】:
Eigen::MatrixXd matrix_ad_; // 矩阵Ad
Eigen::MatrixXd matrix_bd_; // 矩阵Bd
Eigen::MatrixXd matrix_state_; // 状态量x
// 关于【LQR控制器】和【代价函数J】:
Eigen::MatrixXd matrix_k_; // 矩阵K
Eigen::MatrixXd matrix_r_; // 矩阵R
Eigen::MatrixXd matrix_q_; // 矩阵Q
Eigen::MatrixXd matrix_q_updated_;
int lqr_max_iteration_ = 0; // 里卡提方程求解P矩阵时的最大迭代次数
double lqr_eps_ = 0.0; // 里卡提方程求解P矩阵时的收敛精度要求
// 其他:
double ref_curv_; // 目标曲率:当前目标点处的曲率
bool enable_look_ahead_back_control_ = false;
double previous_lateral_acceleration_ = 0.0;
double previous_heading_rate_ = 0.0;
double previous_ref_heading_rate_ = 0.0;
double previous_heading_acceleration_ = 0.0;
double previous_ref_heading_acceleration_ = 0.0;
std::ofstream steer_log_file_;
const std::string name_;
double query_relative_time_;
double pre_steer_angle_ = 0.0;
double pre_steering_position_ = 0.0;
double minimum_speed_protection_ = 0.1;
double current_trajectory_timestamp_ = -1.0;
double init_vehicle_x_ = 0.0;
double init_vehicle_y_ = 0.0;
double init_vehicle_heading_ = 0.0;
double low_speed_bound_ = 0.0;
double low_speed_window_ = 0.0;
double driving_orientation_ = 0.0;
double steer_offset_ = 0.0;
public:
double ref_curv_front_; // 前瞻曲率:视窗中最后一个点的曲率
};
#endif源码文件:
#include "carla_shenlan_lqr_pid_controller/lqr_controller.h"
#include <algorithm>
#include <iomanip>
#include <utility>
#include <vector>
#include "Eigen/LU"
#include "math.h"
using namespace std;
LqrController::LqrController() {}
LqrController::~LqrController() {}
// 函数作用:初始化车辆横向动力学模型(误差型)涉及的各个配置参数 + 初始化LQR涉及的参数
void LqrController::LoadControlConf() {
ts_ = 0.01; // 每隔0.01s进行一次控制
cf_ = 155494.663; // 前轮侧偏刚度,左右轮之和
cr_ = 155494.663; // 后轮侧偏刚度,左右轮之和
wheelbase_ = 2.852; // 车辆纵轴长度
steer_ratio_ = 16; // 方向盘的转角到轮胎转动角度之间的比值系数
steer_single_direction_max_degree_ = 470.0; // 最大方向盘转角
const double mass_fl = 1845.0/4; // 左前悬的质量
const double mass_fr = 1845.0/4; // 右前悬的质量
const double mass_rl = 1845.0/4; // 左后悬的质量
const double mass_rr = 1845.0/4; // 右后悬的质量
const double mass_front = mass_fl + mass_fr; // 前悬质量
const double mass_rear = mass_rl + mass_rr; // 后悬质量
mass_ = mass_front + mass_rear; // 总车质量
lf_ = wheelbase_ * (1.0 - mass_front / mass_); // 汽车前轮到中心点的距离
lr_ = wheelbase_ * (1.0 - mass_rear / mass_); // 汽车后轮到中心点的距离
iz_ = lf_ * lf_ * mass_front + lr_ * lr_ * mass_rear; // 汽车的转动惯量
lqr_eps_ = 0.01; // LQR的迭代求解精度
lqr_max_iteration_ = 1500; // LQR的迭代次数
return;
}
// 函数作用:初始化车辆横向动力学模型(误差型)的状态空间方程 + 初始化LQR涉及的矩阵
void LqrController::Init() {
const int matrix_size = basic_state_size_; // 为4,即状态量x的维数
/* A matrix (Gear Drive)
| 0.0, 1.0, 0.0, 0.0; |
| 0.0, (-(c_f + c_r) / m) / v, (c_f + c_r) / m, (l_r * c_r - l_f * c_f) / m / v; |
| 0.0, 0.0, 0.0, 1.0; |
| 0.0, ((lr * cr - lf * cf) / i_z) / v, (l_f * c_f - l_r * c_r) / i_z, (-1.0 * (l_f^2 * c_f + l_r^2 * c_r) / i_z) / v; | */
// 初始化矩阵A
matrix_a_ = Matrix::Zero(basic_state_size_, basic_state_size_); // 初始化:连续状态空间方程的矩阵A
matrix_ad_ = Matrix::Zero(basic_state_size_, basic_state_size_); // 初始化:离散状态空间方程的矩阵Ad
// 初始化A矩阵的常数项(矩阵A中不带v的项)(注意:这个v指的是车辆速度的x轴上的分量值vx,这是一个常量)
matrix_a_(0, 1) = 1.0;
matrix_a_(1, 2) = (cf_ + cr_) / mass_;
matrix_a_(2, 3) = 1.0;
matrix_a_(3, 2) = (lf_ * cf_ - lr_ * cr_) / iz_;
// 初始化A矩阵的非常数项(矩阵A中带v的项)
matrix_a_coeff_ = Matrix::Zero(matrix_size, matrix_size);
matrix_a_coeff_(1, 1) = -(cf_ + cr_) / mass_;
matrix_a_coeff_(1, 3) = (lr_ * cr_ - lf_ * cf_) / mass_;
matrix_a_coeff_(3, 1) = (lr_ * cr_ - lf_ * cf_) / iz_;
matrix_a_coeff_(3, 3) = -1.0 * (lf_ * lf_ * cf_ + lr_ * lr_ * cr_) / iz_;
/* B matrix
| 0.0, c_f / m, 0.0, l_f * c_f / i_z; | */
// 初始化B矩阵
matrix_b_ = Matrix::Zero(basic_state_size_, 1); // 初始化:连续状态空间方程的矩阵B
matrix_bd_ = Matrix::Zero(basic_state_size_, 1); // 初始化:离散状态空间方程的矩阵Bd
matrix_b_(1, 0) = cf_ / mass_;
matrix_b_(3, 0) = lf_ * cf_ / iz_;
// 状态向量x
matrix_state_ = Matrix::Zero(matrix_size, 1);
// 反馈矩阵K
matrix_k_ = Matrix::Zero(1, matrix_size);
// 代价函数中的R矩阵(输入值u的权重)
matrix_r_ = Matrix::Identity(1, 1);
matrix_r_(0, 0) = 10;
// 代价函数中的Q矩阵(状态向量x的权重)
matrix_q_ = Matrix::Zero(matrix_size, matrix_size);
matrix_q_(0, 0) = 2; // TODO: lateral_error 横向误差 对应的参数
matrix_q_(1, 1) = 1; // TODO: lateral_error_rate 横向误差变化率 对应的参数
matrix_q_(2, 2) = 0.1; // TODO: heading_error 航向角误差 对应的参数
matrix_q_(3, 3) = 0.1; // TODO: heading_error_rate 航向角误差变化率 对应的参数
matrix_q_updated_ = matrix_q_;
return;
}
// 函数作用:计算目标点和车辆质心之间距离的平方
double PointDistanceSquare(const TrajectoryPoint &point, const double x, const double y) {
double dx = point.x - x;
double dy = point.y - y;
return dx * dx + dy * dy;
}
// 函数作用:将弧度值归化到 [-M_PI, M_PI] 之间,防止弧度值超过量纲
double NormalizeAngle(const double angle) {
double a = std::fmod(angle + M_PI, 2.0 * M_PI);
if (a < 0.0) a += (2.0 * M_PI);
return a - M_PI;
}
// 函数作用:将角度化为弧度
double atan2_to_PI(const double atan2) { return atan2 * M_PI / 180; }
// **TODO **计算控制命令
// 注意:该函数定频调用(每隔时间ts_就调用一次)
bool LqrController::ComputeControlCommand(const VehicleState &localization, const TrajectoryData &planning_published_trajectory, ControlCmd &cmd) {
// 目标轨迹
trajectory_points_ = planning_published_trajectory.trajectory_points;
// TODO 01 配置状态矩阵A
// matrix_a_ = matrix_a_ + matrix_a_coeff_ / localization.vx;
matrix_a_(1, 1) = matrix_a_coeff_(1, 1) / v;
matrix_a_(1, 3) = matrix_a_coeff_(1, 3) / v;
matrix_a_(3, 1) = matrix_a_coeff_(3, 1) / v;
matrix_a_(3, 3) = matrix_a_coeff_(3, 3) / v;
// TODO 02 将矩阵B离散化为Bd
matrix_bd_ = matrix_b_ * ts_;
cout << "matrix_bd_.row(): " << matrix_bd_.rows() << endl;
cout << "matrix_bd_.col(): " << matrix_bd_.cols() << endl;
// Update state = [Lateral Error, Lateral Error Rate, Heading Error, Heading Error Rate]
// TODO 03 计算状态向量x的4个误差分量的值
UpdateState(localization);
// TODO 04 将状态矩阵A离散化为Ad
UpdateMatrix(localization);
// TODO 05 求解里卡提方程中的P矩阵 + 求解LQR控制器中的反馈矩阵K
SolveLQRProblem(matrix_ad_, matrix_bd_, matrix_q_, matrix_r_, lqr_eps_, lqr_max_iteration_, &matrix_k_);
// TODO 06 计算反馈控制
std::cout << "matrix_k_: " << matrix_k_ << std::endl;
double steer_angle_feedback = 0;
steer_angle_feedback = -(matrix_k_(0,0) * matrix_state_(0,0) + matrix_k_(0,1) * matrix_state_(1,0) + matrix_k_(0,2) * matrix_state_(2,0) + matrix_k_(0,3) * matrix_state_(3,0));
// TODO 07 计算前馈控制
double steer_angle_feedforward = 0.0;
steer_angle_feedforward = ComputeFeedForward(localization, ref_curv_);
std::cout << "steer_angle_feedforward:\t" << steer_angle_feedforward << std::endl;
// 计算控制器应该输出的方向盘转角
double steer_angle = steer_angle_feedback - 0.9 * steer_angle_feedforward;
std::cout << "steer_angle Inital:\t" << steer_angle << std::endl;
// 限制前轮最大转角,这里定义前轮最大转角位于 [-20度~20度] 之间
if (steer_angle >= atan2_to_PI(20.0)) steer_angle = atan2_to_PI(20.0);
else if (steer_angle <= -atan2_to_PI(20.0)) steer_angle = -atan2_to_PI(20.0);
// 输出控制命令给Carla仿真器(注意:输出的内容为弧度)
// 注意:在全局坐标系中转向角大于0即左转,但是在Carla仿真器中转向角大于0为右转,所以因为Carla的控制命令和全局坐标系下的控制命令是相反的,输出需要乘上-1
cmd.steer_target = -1 * steer_angle;
std::cout << "steer_angle Normalize:\t" << steer_angle << std::endl;
return true;
}
// TODO 03 函数作用:计算状态向量x的4个分量
void LqrController::UpdateState(const VehicleState &vehicle_state) {
// 创建一个 LateralControlError 类的共享智能指针 lat_con_err
std::shared_ptr<LateralControlError> lat_con_err = std::make_shared<LateralControlError>();
// 计算横向误差
ComputeLateralErrors(vehicle_state.x, vehicle_state.y, vehicle_state.heading, vehicle_state.vx, vehicle_state.vy, vehicle_state.angular_velocity, vehicle_state.acceleration, lat_con_err);
// 更新车辆横向动力学模型(误差型)中的状态量x
matrix_state_(0, 0) = lat_con_err->lateral_error;
matrix_state_(1, 0) = lat_con_err->lateral_error_rate;
matrix_state_(2, 0) = lat_con_err->heading_error;
matrix_state_(3, 0) = lat_con_err->heading_error_rate;
cout << "lateral_error: " << (lat_con_err->lateral_error) << endl;
cout << "heading_error: " << (lat_con_err->heading_error) << endl;
}
// TODO 03 函数作用:计算状态向量x所需要的4个误差量的值
void LqrController::ComputeLateralErrors(const double x, const double y, const double theta, const double vx, const double vy, const double angular_v, const double linear_a, LateralControlErrorPtr &lat_con_err) {
TrajectoryPoint nearest_point = QueryNearestPointByPosition(x, y);
double ref_theta = nearest_point.heading; // 目标点的航向角
double kappa = nearest_point.kappa; // 目标点的曲率
double dx = nearest_point.x - x;
double dy = nearest_point.y - y;
// 注意:这里使用的计算横向误差和航向误差的公式,都是老王课上讲的,而不是深蓝的课上讲的,老王的课上讲的才是精确推导公式,而深蓝课上讲的则是粗略推导
double e_theta = NormalizeAngle(theta - ref_theta); // 航向误差:
double e_d = (x - nearest_point.x) * (-1 * sin(ref_theta)) + (y - nearest_point.y)* cos(ref_theta); // 横向误差:
double s_dot = (vx * cos(e_theta) - vy * sin(e_theta)) / (1 - kappa * e_d) // 质心在目标路径上的投影的纵向速度(即 vx(s) )
double e_theta_dot = angular_v - kappa * s_dot; // 航向误差变化率:
double e_d_dot = vy * cos(e_theta) + vx * sin(e_theta); // 横向误差变化率:
lat_con_err->lateral_error = e_d; // 横向误差
lat_con_err->lateral_error_rate = e_d_dot; // 横向误差变化率
lat_con_err->heading_error = e_theta; // 航向误差
lat_con_err->heading_error_rate = e_theta_dot; // 航向误差变化率
}
// TODO 03 函数作用:查询距离当前车辆质心最近的轨迹点作为目标点
TrajectoryPoint LqrController::QueryNearestPointByPosition(const double x, const double y) {
double d_min = PointDistanceSquare(trajectory_points_.front(), x, y);
size_t index_min = 0;
for (size_t i = 1; i < trajectory_points_.size(); ++i) {
double d_temp = PointDistanceSquare(trajectory_points_[i], x, y);
if (d_temp < d_min) {
d_min = d_temp;
index_min = i;
}
}
ref_curv_ = trajectory_points_[index_min].kappa; // 目标曲率:目标点处的曲率
double front_index = index_min + 5; // 多点预瞄:定义视窗的长度为6,1个当前目标点和5个未来目标点
if (front_index >= trajectory_points_.size()) { // 前瞻曲率:视窗中最后一个点的曲率
ref_curv_front_ = trajectory_points_[index_min].kappa;
} else {
ref_curv_front_ = trajectory_points_[front_index].kappa;
}
return trajectory_points_[index_min];
}
// TODO 04 函数作用:将状态矩阵A离散化为Ad
void LqrController::UpdateMatrix(const VehicleState &vehicle_state) {
// double v = std::max(vehicle_state.velocity, minimum_speed_protection_);
Matrix I = Matrix::Identity(basic_state_size_, basic_state_size_);
matrix_ad_ = (I - matrix_a_ * ts_ * 0.5).inverse() * (I + matrix_a_ * ts_ * 0.5);
}
// TODO 05 函数作用:求解里卡提方程中的P矩阵 + 求解LQR控制器中的反馈矩阵K
void LqrController::SolveLQRProblem(const Matrix &A, const Matrix &B, const Matrix &Q, const Matrix &R, const double tolerance, const uint max_num_iteration, Matrix *ptr_K) {
// 防止矩阵的维数出错导致后续的运算失败
if (A.rows() != A.cols() || B.rows() != A.rows() || Q.rows() != Q.cols() || Q.rows() != A.rows() || R.rows() != R.cols() || R.rows() != B.cols()) {
std::cout << "LQR solver: one or more matrices have incompatible dimensions." << std::endl;
return;
}
// 解释:对里卡提方程方程的求解其实是一个迭代求解P矩阵的过程,只有当对P矩阵的求解收敛到一定精度的时候,才相当于求出了P矩阵
Matrix P = Matrix::Zero(basic_state_size_, basic_state_size_);
Matrix P_next = Matrix::Zero(basic_state_size_, basic_state_size_);
Matrix AT = A.transpose();
Matrix BT = B.transpose();
double diff = 0; // 作为标志判断里卡提方程是否收敛,该标志位为前后两个迭代过程中两个P矩阵之间差距最大的元素的差值
for (uint i = 0; i < max_num_iteration; ++i) {
P_next = (AT*P*A) - (AT*P*B) * (R+BT*P*B).inverse() * (BT*P*A) + Q;
diff = fabs((P_next - P).maxCoeff());
P = P_next;
if (diff < tolerance) {
std::cout << "diff = " << diff << std::endl;
*ptr_K = (R + BT*P*B).inverse() * (BT*P*A);
return;
}
}
std::cout << "failed to solver riccati in max" << max_num_iteration << std::endl;
}
// TODO 07 函数作用:计算前馈控制(加入前馈,是因为我们使用的误差形式的状态空间方程是有三项的,我们只是使用LQR控制了前两项,对于后面的那个小尾巴则没有对应的控制,前馈就是为了解决这个问题而加上的)
double LqrController::ComputeFeedForward(const VehicleState &localization, double ref_curvature) {
if (isnan(ref_curvature)) ref_curvature= 0;
double kv = (lr_ * mass_ / (2 * cf_ * (lf_ + lr_))) - (lf_ * mass_ / (2 * cr_ * (lf_ + lr_)));
double v = localization.velocity;
double steer_angle_feedforward = ref_curvature * wheelbase_ + kv * v * v * ref_curvature - matrix_k_(0,2) * ref_curvature * (lr_ - lf_ * mass_ * v * v / (2 * cr_ * wheelbase_));
return steer_angle_feedforward;
}4.5.2 参考线(reference line)-- 代码
注意1:这里用来计算得到参考线的算法比较粗糙,使用的方法是【直接把全局路径规划得到的目标路径作为参考线】;
- 而全局路径的每个路径点只有基础的位置信息;
- 但是参考线上的每个路径点所需要的不仅仅是坐标,还有其他的几何信息(如曲率,曲率变化率...);
a
注意2:因此需要将全局路径信息进行进一步的处理,使得每个路径点都包含以下五种信息
- 位置坐标(全局坐标系中的坐标)
- 朝向角
- 路径长度
- 曲率
- 曲率变化率
补充:Apollo中使用的参考线算法则更精细,大致思路一样,也是将全局规划路径作为参考线,但是加入了很多额外的优化;
- 分段剪裁出参考线,对这一段参考线进行平滑
- 将平滑后的参考线进行拼接,且每一段在相接处差别不大,保证了参考线的前后一致性
注:以下是粗略的实现方法的代码
头文件:
#ifndef REFERENCE_LINE_H_
#define REFERENCE_LINE_H_
#include <math.h>
#include <iostream>
#include <vector>
class ReferenceLine {
public:
ReferenceLine(const std::vector<std::pair<double, double>> &xy_points);
~ReferenceLine() = default;
// 函数作用:计算参考线。参考线的每个点需要包含以下信息
// 1) xy_pionts_ 路径点坐标
// 2) headings 路径点朝向角
// 3) accumulated_s 路径点累计路程
// 4) kappas 路径点曲率
// 5) dkappas 路径点曲率的变化率
bool ComputePathProfile(std::vector<double> *headings, std::vector<double> *accumulated_s, std::vector<double> *kappas, std::vector<double> *dkappas);
private:
std::vector<std::pair<double, double>> xy_points_; // 用vector装载规划的全局路径上所有点的坐标
};
#endif源文件:
#include "carla_shenlan_lqr_pid_controller/reference_line.h"
// 函数作用:拷贝构造函数
ReferenceLine::ReferenceLine(const std::vector<std::pair<double, double>>& xy_points) { xy_points_ = xy_points; }
// 函数作用:由于全局路径规划期仅仅给出了全局路径信息(即所有点的xy坐标),而没有任何关于这条全局路径的其他几何信息(如每个路径点的 朝向角/距离/曲率/曲率变化率);
// 而我们在局部规划中使用的参考线其实是和全局路径重合的,也就是说参考线上的所有路径点就是全局路径的所有路径点;
// 但是要注意,我们需要的参考线不能仅仅只有每个路径点的坐标,还需要有每个路径点的各个几何信息(如 朝向角/距离/曲率/曲率变化率);
// 因此我们直接计算全局路径中每个路径点的几何信息,然后汇总到一起,就是我们需要的参考线信息;
bool ReferenceLine::ComputePathProfile(std::vector<double>* headings, std::vector<double>* accumulated_s, std::vector<double>* kappas, std::vector<double>* dkappas) {
headings->clear(); // 装载每个路径点的 -- 朝向角
accumulated_s->clear(); // 装载每个路径点的 -- 到达该点时所累积的路径长度(起点到该点的几何路径长度)
kappas->clear(); // 装载每个路径点的 -- 曲率
dkappas->clear(); // 装载每个路径点的 -- 曲率变化率
if (xy_points_.size() < 2) return false;
std::vector<double> dxs; // 路径点处的 -- dx
std::vector<double> dys; // 路径点处的 -- dy
std::vector<double> y_over_s_first_derivatives; // 路径点处的 -- 一阶偏x导数
std::vector<double> x_over_s_first_derivatives; // 路径点处的 -- 一阶偏y导数
std::vector<double> y_over_s_second_derivatives; // 路径点处的 -- 二阶偏x导数
std::vector<double> x_over_s_second_derivatives; // 路径点处的 -- 二阶偏y导数
// 计算每个路径点的x,y差值(即dx,dy)
std::size_t points_size = xy_points_.size();
for (std::size_t i = 0; i < points_size; ++i) {
double x_delta = 0.0;
double y_delta = 0.0;
if (i == 0) {
x_delta = (xy_points_[i + 1].first - xy_points_[i].first);
y_delta = (xy_points_[i + 1].second - xy_points_[i].second);
} else if (i == points_size - 1) {
x_delta = (xy_points_[i].first - xy_points_[i - 1].first);
y_delta = (xy_points_[i].second - xy_points_[i - 1].second);
} else {
x_delta = 0.5 * (xy_points_[i + 1].first - xy_points_[i - 1].first);
y_delta = 0.5 * (xy_points_[i + 1].second - xy_points_[i - 1].second);
}
dxs.push_back(x_delta);
dys.push_back(y_delta);
}
// 计算每个路径点的朝向角
for (std::size_t i = 0; i < points_size; ++i) {
headings->push_back(std::atan2(dys[i], dxs[i]));
}
// 计算每个路径点处的累计路径长度
double distance = 0.0;
accumulated_s->push_back(distance); // 第一个路径点(起点)的 index = 0 ,且在该点处的累计路径长度为 0
double fx = xy_points_[0].first; // 起点横坐标
double fy = xy_points_[0].second; // 起点纵坐标
double nx = 0.0;
double ny = 0.0;
for (std::size_t i = 1; i < points_size; ++i) {
nx = xy_points_[i].first;
ny = xy_points_[i].second;
double end_segment_s = std::sqrt((fx - nx) * (fx - nx) + (fy - ny) * (fy - ny));
accumulated_s->push_back(end_segment_s + distance);
distance += end_segment_s;
fx = nx;
fy = ny;
}
// 计算每个路径点相对于路径长度ds的x和y的一阶导数
for (std::size_t i = 0; i < points_size; ++i) {
double xds = 0.0;
double yds = 0.0;
if (i == 0) {
xds = (xy_points_[i + 1].first - xy_points_[i].first) / (accumulated_s->at(i + 1) - accumulated_s->at(i));
yds = (xy_points_[i + 1].second - xy_points_[i].second) / (accumulated_s->at(i + 1) - accumulated_s->at(i));
} else if (i == points_size - 1) {
xds = (xy_points_[i].first - xy_points_[i - 1].first) / (accumulated_s->at(i) - accumulated_s->at(i - 1));
yds = (xy_points_[i].second - xy_points_[i - 1].second) / (accumulated_s->at(i) - accumulated_s->at(i - 1));
} else {
xds = (xy_points_[i + 1].first - xy_points_[i - 1].first) / (accumulated_s->at(i + 1) - accumulated_s->at(i - 1));
yds = (xy_points_[i + 1].second - xy_points_[i - 1].second) / (accumulated_s->at(i + 1) - accumulated_s->at(i - 1));
}
x_over_s_first_derivatives.push_back(xds);
y_over_s_first_derivatives.push_back(yds);
}
// 计算每个路径点相对于路径长度ds的x和y的二阶导数
for (std::size_t i = 0; i < points_size; ++i) {
double xdds = 0.0;
double ydds = 0.0;
if (i == 0) {
xdds = (x_over_s_first_derivatives[i + 1] - x_over_s_first_derivatives[i]) / (accumulated_s->at(i + 1) - accumulated_s->at(i));
ydds = (y_over_s_first_derivatives[i + 1] - y_over_s_first_derivatives[i]) / (accumulated_s->at(i + 1) - accumulated_s->at(i));
} else if (i == points_size - 1) {
xdds = (x_over_s_first_derivatives[i] - x_over_s_first_derivatives[i - 1]) / (accumulated_s->at(i) - accumulated_s->at(i - 1));
ydds = (y_over_s_first_derivatives[i] - y_over_s_first_derivatives[i - 1]) / (accumulated_s->at(i) - accumulated_s->at(i - 1));
} else {
xdds = (x_over_s_first_derivatives[i + 1] - x_over_s_first_derivatives[i - 1]) / (accumulated_s->at(i + 1) - accumulated_s->at(i - 1));
ydds = (y_over_s_first_derivatives[i + 1] - y_over_s_first_derivatives[i - 1]) / (accumulated_s->at(i + 1) - accumulated_s->at(i - 1));
}
x_over_s_second_derivatives.push_back(xdds);
y_over_s_second_derivatives.push_back(ydds);
}
// 计算每个路径点处的曲率
for (std::size_t i = 0; i < points_size; ++i) {
double xds = x_over_s_first_derivatives[i];
double yds = y_over_s_first_derivatives[i];
double xdds = x_over_s_second_derivatives[i];
double ydds = y_over_s_second_derivatives[i];
double kappa = (xds * ydds - yds * xdds) / (std::sqrt(xds * xds + yds * yds) * (xds * xds + yds * yds) + 1e-6);
// 注1:曲率计算公式的分母上加上一个很小的数,防止除法失效
// 注2:这里对曲率的计算使用的是精确公式,而代码中我们在进行动力学建模,计算连续误差型状态空间方程的状态量x时(如:航向误差变化率)。则是将曲率视为了半径的倒数,这是一种对曲率的估算方式;
kappas->push_back(kappa);
}
// 计算每个路径点处的曲率变化率
for (std::size_t i = 0; i < points_size; ++i) {
double dkappa = 0.0;
if (i == 0) {
dkappa = (kappas->at(i + 1) - kappas->at(i)) / (accumulated_s->at(i + 1) - accumulated_s->at(i));
} else if (i == points_size - 1) {
dkappa = (kappas->at(i) - kappas->at(i - 1)) / (accumulated_s->at(i) - accumulated_s->at(i - 1));
} else {
dkappa = (kappas->at(i + 1) - kappas->at(i - 1)) / (accumulated_s->at(i + 1) - accumulated_s->at(i - 1));
}
dkappas->push_back(dkappa);
}
return true;
}4.5.3 ROS与Carla联合仿真 -- 代码
注意1:主函数在这一部分;
注意2:在联合仿真时,使用PID控制车辆纵向,使用LQR控制车辆横向;
头文件:
源文件:










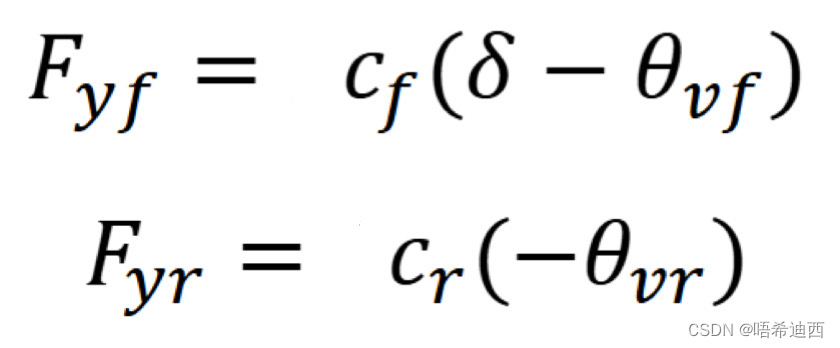
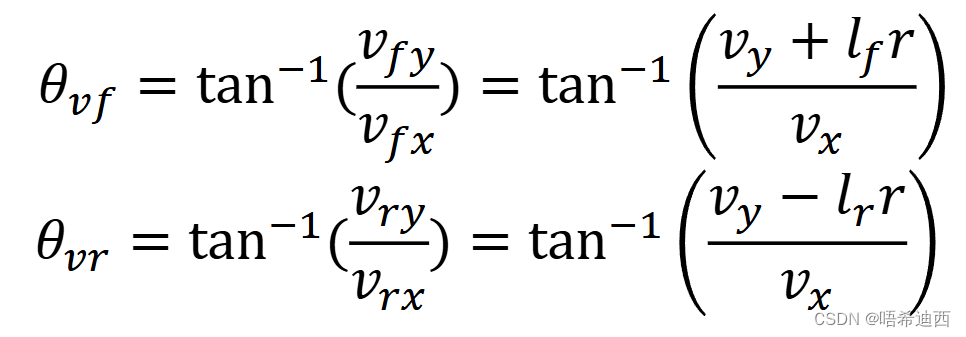












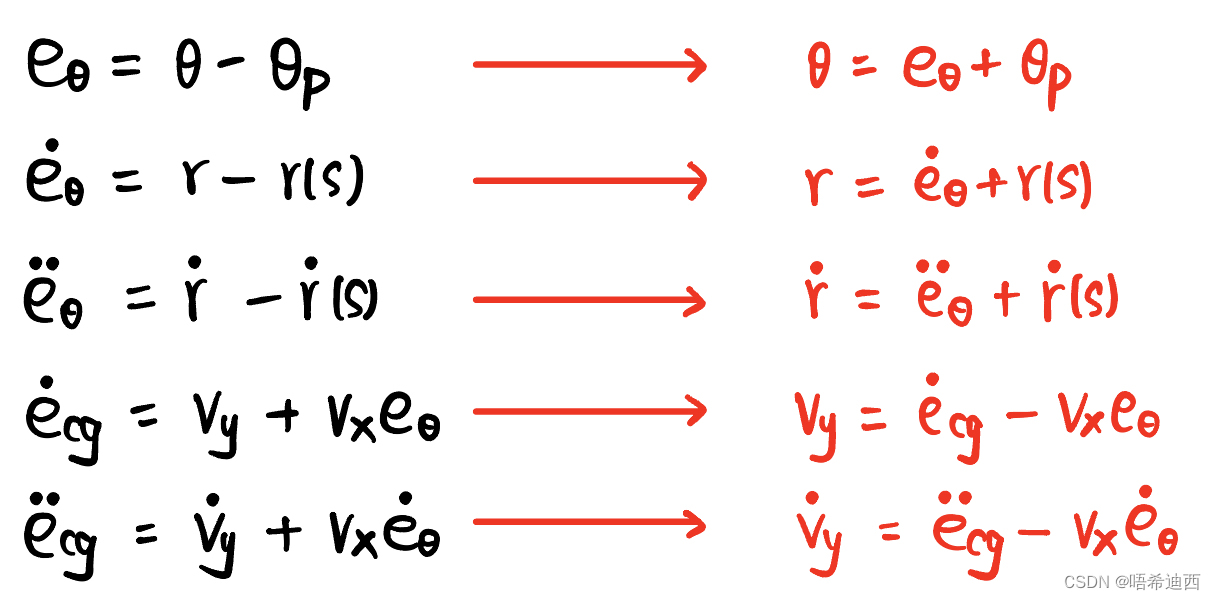
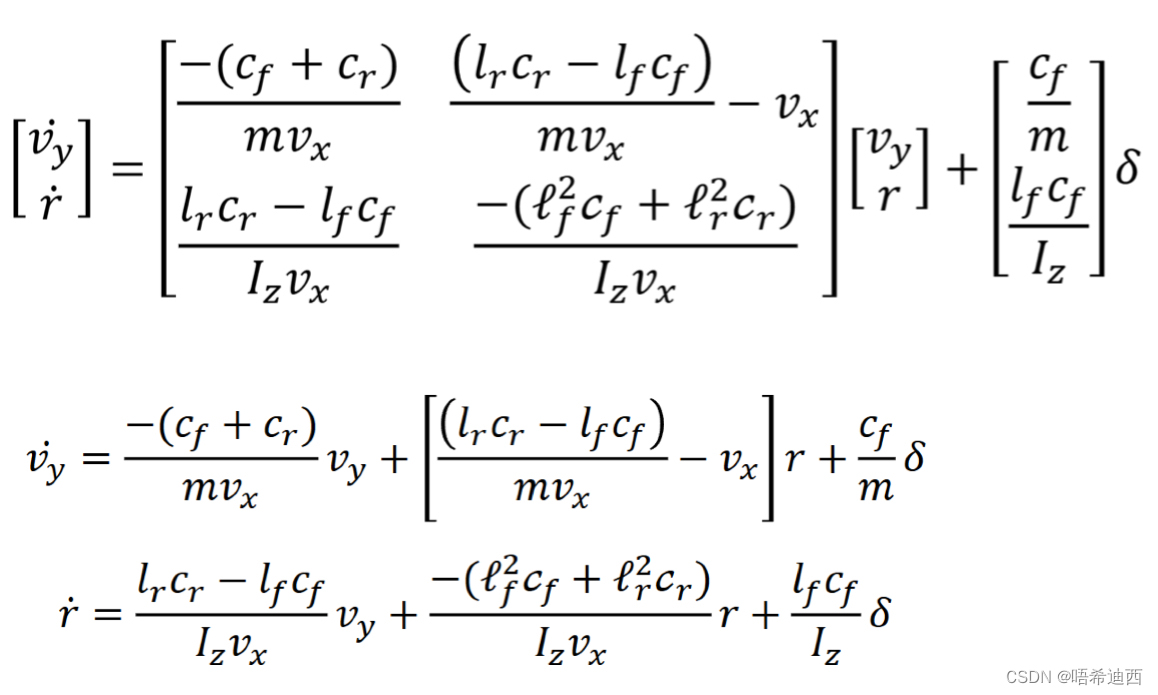
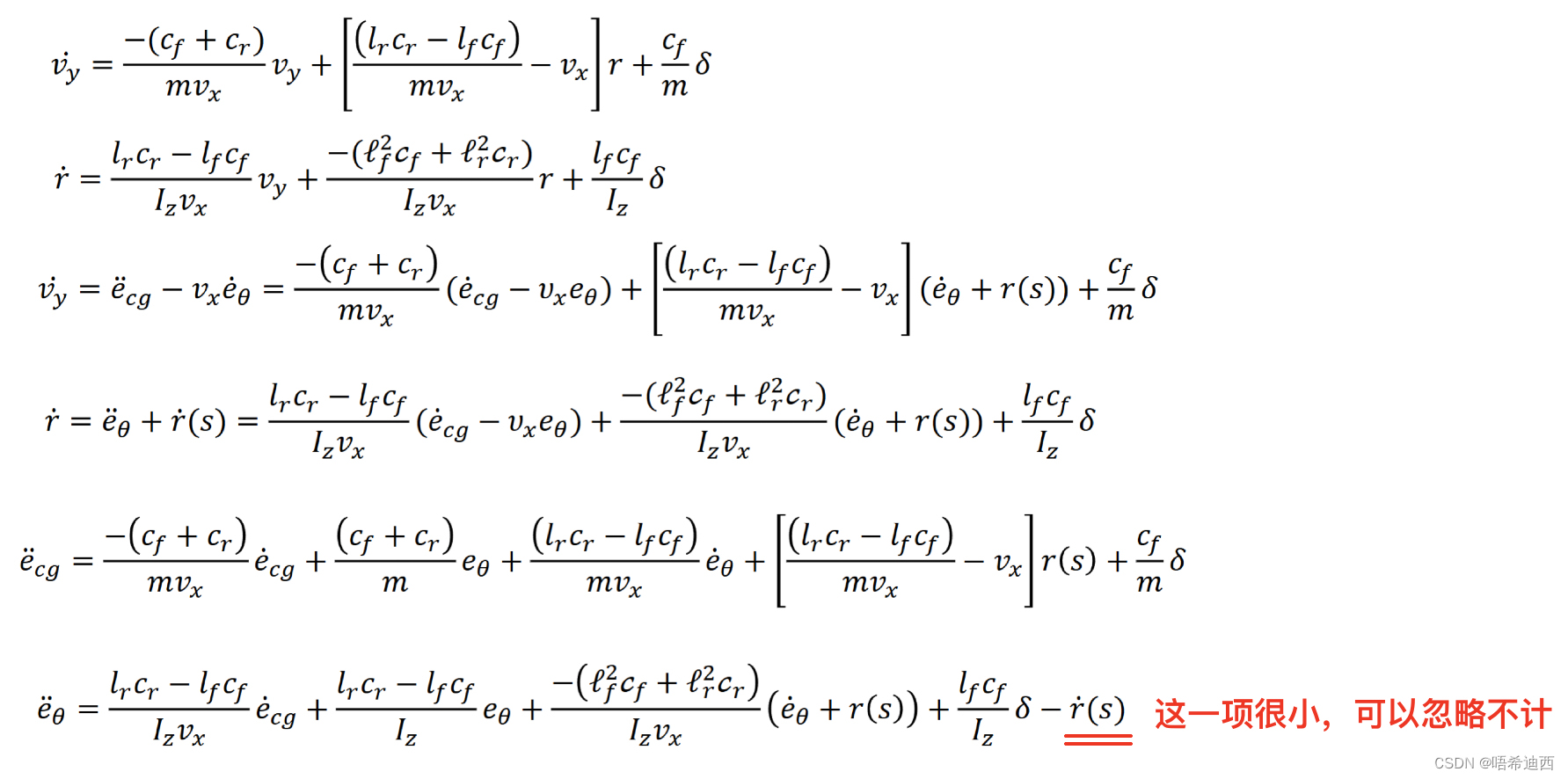
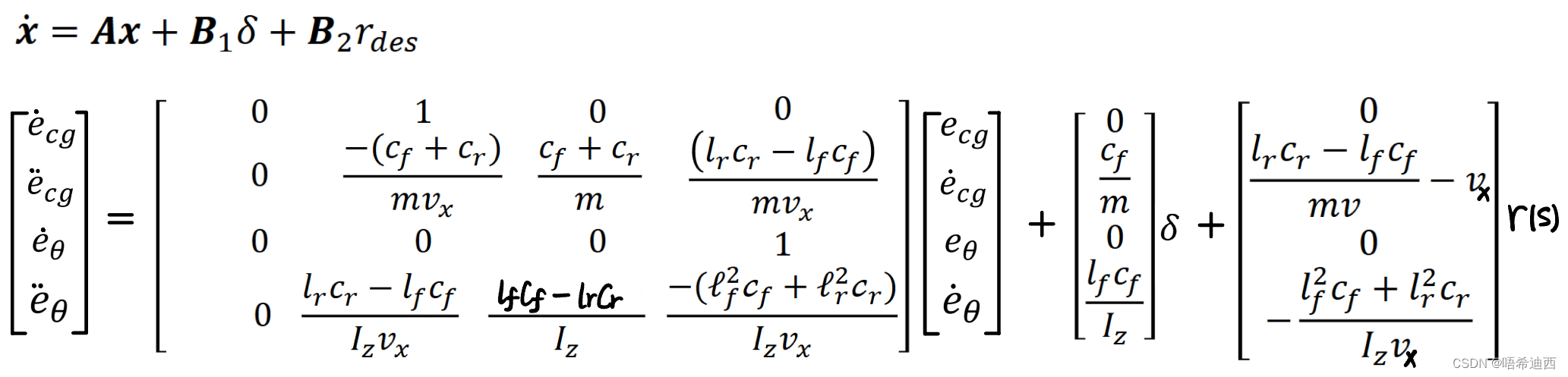

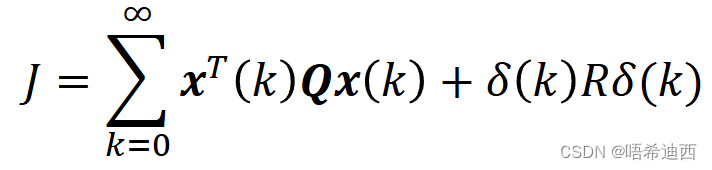




















 9023
9023

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








