3.1 车辆横向运动学模型
注:上一篇博客讲解了车辆的纵向运动控制,这一篇博客将要讲解的是车辆的横向运动控制;横向运动控制主要是控制车辆一直保持在期望的轨迹上行驶(即通过打方向盘保证车辆的横向运动方向符合预期),同时要保证对车辆的横向控制(打方向盘的程度)满足车辆的动力学特性;
3.1.1 自行车模型
注:如果想控制车辆的运动,那首先要对车辆的运动建立一个数据化的模型,自行车模型是一个非常常见且简单的车辆模型,我们通过自行车模型,来建立车辆的横向运动控制模型(运动学模型)

:车辆质心
:车辆纵向轴距(
为质心离前轮的轴距,
为质心离后轮的轴距)
:车辆的质心速度,代表车辆在行驶过程中的实际速度
:横摆角(车纵轴与X轴的夹角),代表车辆的行驶方向
:质心侧偏角(车纵轴与车速
之间的夹角)
:前轮转角(后轮转角
在图中未体现)
在通过自行车模型建立车辆运动学模型的时候,做出的假设:
- 忽略车辆在垂直方向(Z轴)上的运动,我们对车辆的描述是在一个二维平面上进行的;
- 假设车辆的两个前轮/两个后轮的转角和转速是相同的,且假设车辆转向角很小,这样我们可以将车辆的两个前轮/后轮用一个前轮/后轮来代替,因为两个前轮/后轮的性质是相同的,这样就可以将一个四轮车模型简化为一个两轮车模型;(而实际上两个轮胎的转角是不相同的,车辆的转角越大,内外侧轮胎的转向角差值越大,所以为了使用自行车模型,必须保证车辆的转向角比较小)(后面的阿克曼转向几何进行了具体讲解)
- 忽略了轮胎受到的侧向力,即假设前轮转角
和前轮轮速
的方向是一致的,后轮也是这样;不过这个假设成立的条件为低速行驶,因为只有在低速行驶的时候,轮胎产生的侧向力很小可以忽略,所以可以大致认为前轮转角
和前轮轮速
的方向一致;
- 假设车辆的行驶速度的变化也是缓慢的(即加速度很小),这样我们就可以忽略掉车辆前后轴的载荷转移;
- 假设整车以及悬架系统是刚性的,即车轮是没有滑移运动的,因此可以使用横摆角代表车辆的实际运动方向;
a
a
注:运动学模型仅在低速环境下有效(假设3),如果想要建立高速情况下的车辆横向控制模型,就必须考虑轮胎侧向力,这个时候需要使用车辆动力学模型;
a
a
总结:
- 低速+小转角行车使用运动学模型作为车辆的横向运动控制模型
- 高速行车使用动力学模型作为车辆的横向运动控制模型
3.1.2 车辆的运动学模型
注1:车辆的运动学模型其实就是车辆的横向运动控制模型;
注2:运动学模型建立在大地坐标系(惯性系/绝对坐标系)中,所以我们将自行车模型也放进惯性系中进行分析;
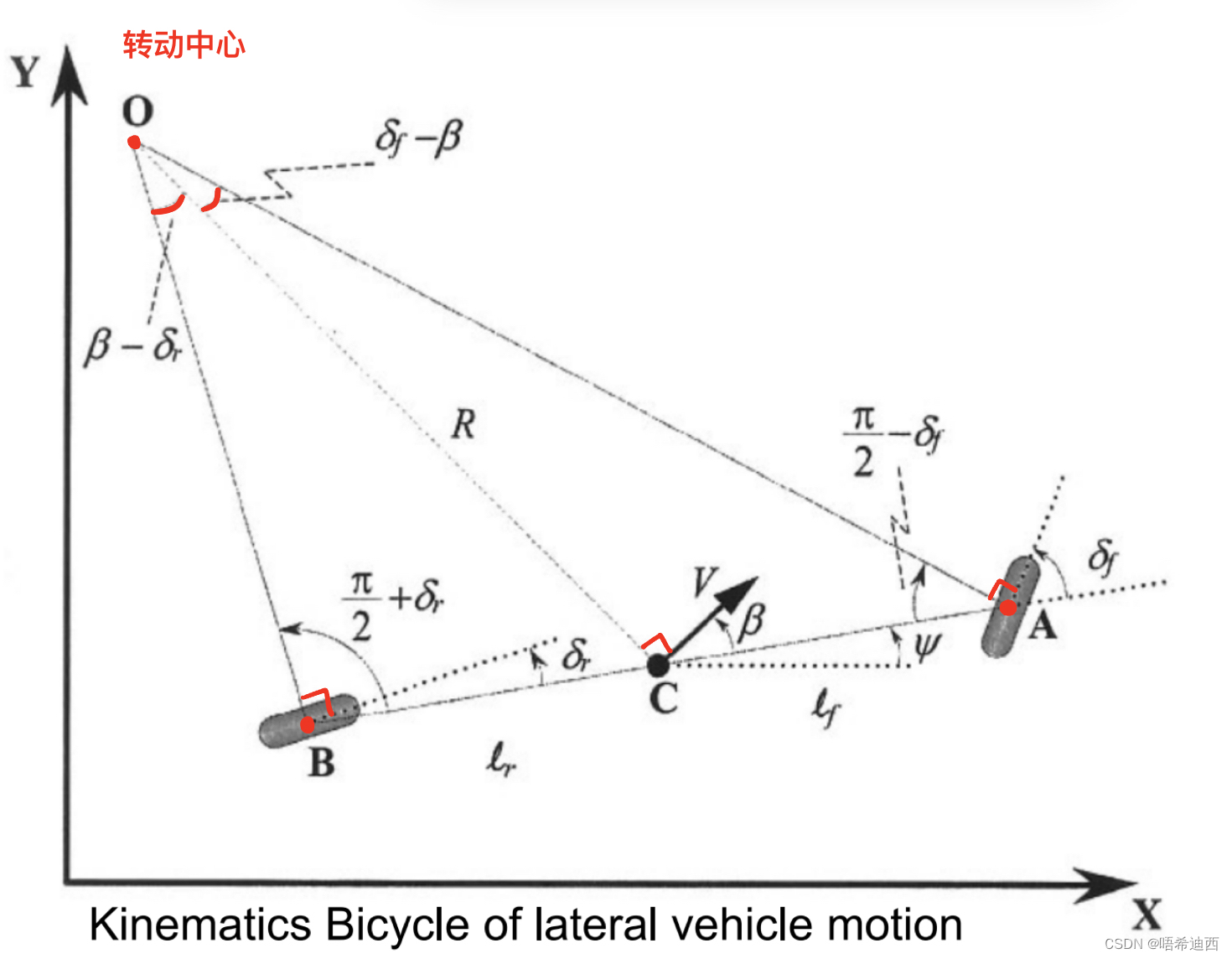
运动学模型推导过程:
注意:有 ,因为一般慢速时质心侧偏角很小,因此记为 0,即
;
最终得到运动学模型:(三个量:X轴车速,Y轴车速,车辆角速度)
a
a
注:
的计算公式是用来代替上述的三个公式中的
变量的,他并不是运动学模型三个方程中的一个;
关于运动学模型的运用:
a
a
- 车辆模型已知量:
- 控制系统输入量:
- 方向盘转角
:用来进行横向控制
- 前轮转角
:给定了方向盘转角
就相当于给定了前轮转角
,因为方向盘转角和前轮转角之间有一个传动比;
- 后轮转角
:一般默认为0;
- 油门/刹车开度:用来进行纵向控制
- 已知状态量:
- 车轴距
- 车速
的大小(但不知道方向,即不知道质心侧偏角
的大小)
- 车辆朝向
(即车辆横摆角)
a
a
- 车辆模型待求量:
- 车直线速度
:带方向的车速,质心侧偏角
用公式计算出来,X轴和Y轴速度用运动学公式计算出来
- 车转向速度
:用运动学公式计算出来
3.1.3 阿克曼转向几何(Ackerman Turning Geometry)
阿克曼转向几何解决的问题:
在此技术出现之前,车辆主要使用单铰链转向技术,转弯时内外轮无法指向同一圆心,两个前轮是平行的,转弯过度容易卡住不动,无法顺滑转弯;
所以阿克曼转向几何的出现是为了解决汽车在转向时,由于左、右转向轮的转向半径不同所造成的左、右转向轮转角不同的问题;根据阿克曼转向几何设计的车辆在沿着弯道转弯时,利用四连杆的相等曲柄(构成一个梯形结构);
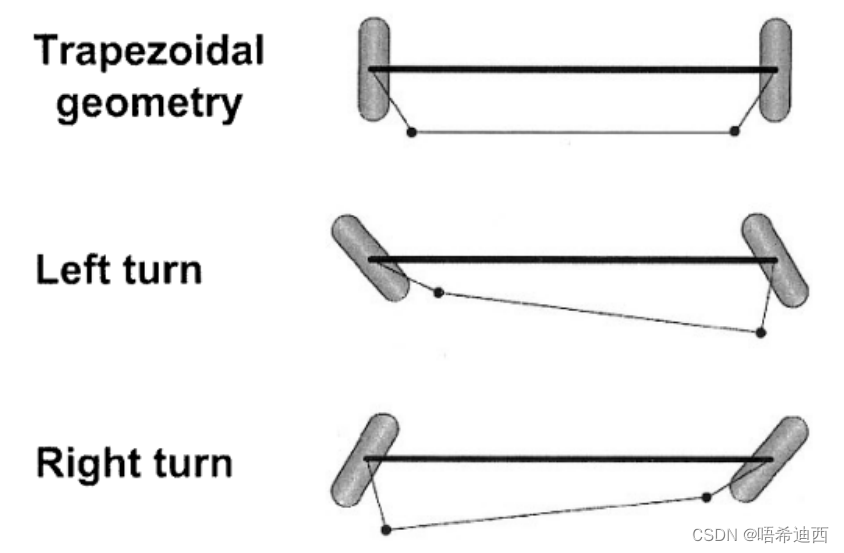
可以使内侧轮的转向角比外侧轮大大约2~4度(内侧轮转向角与外侧轮转向角之间的差被称为阿克曼角),使四个轮子路径的圆心大致交会于后轴的延长线上瞬时转向中心(即同一个圆心);使得汽车在行驶过程中,每个车轮的运动轨迹都必须完全符合它的自然运动轨迹,从而保证轮胎与地面间处于纯滚动而无滑移现象;

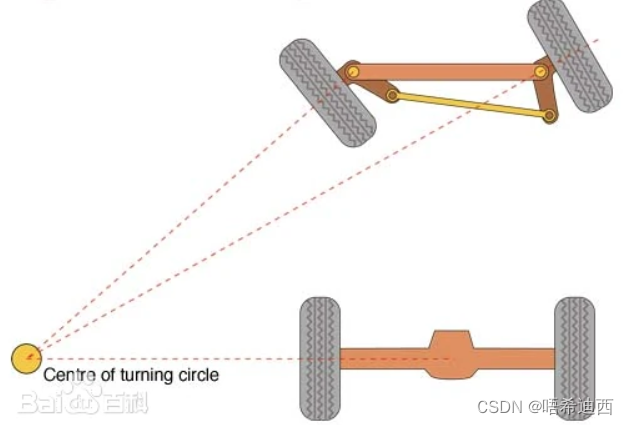

a
a
a
阿克曼转向几何的实际应用:
车辆在转弯时驱动轮应该有不同的轮速,利用阿克曼模型的汽车的驱动方式分为:前驱、后驱和四驱;利用“差速器”这样一个机械结构,将发动机的转速自动分配到两个驱动轮上,使两个驱动轮的速度不同并满足转弯需求;
前驱的差速器显然在前轮上,后驱的差速器在后轮上,四驱的差速器在前后轮均有;
a
a
a
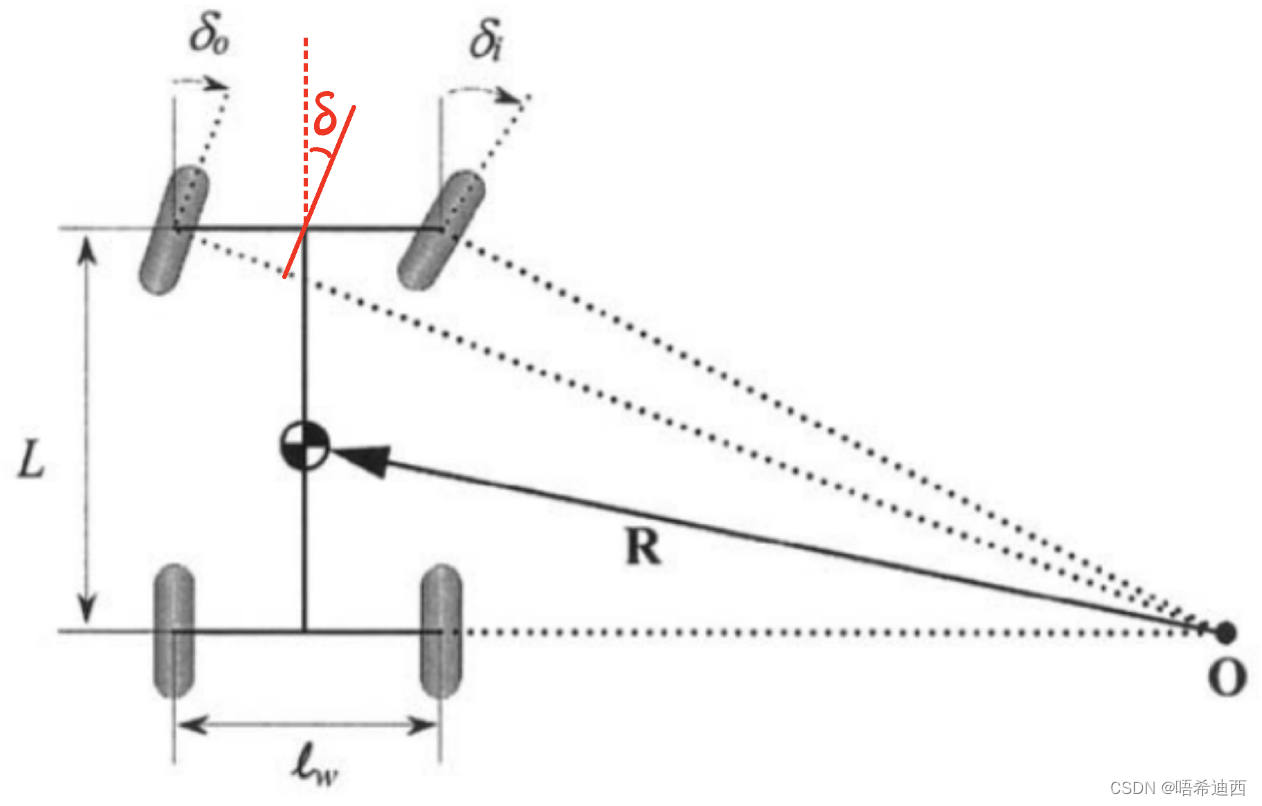
阿克曼转向几何推导:

:即为自行车模型中的前向转角
,其值为
:左前轮转角
:右前轮转角
:车辆转弯半径
:车辆宽度(横向轴距)
:车辆长度(纵向轴距)
a
a
a
注1:车辆的真实转弯半径R是转弯圆心和车辆质心之间的距离,但是这里取的车辆转向半径R是用后轮的转弯半径代替的;
- 原因1:R是远大于车辆的纵向轴距的,所以那一点的偏差可以忽略不计;
- 原因2:阿克曼转向几何要求四个轮子的转向中心位于同一个点,而在阿克曼转向几何的推导中,将后轮视为车辆的转向支点,所以选择后轮的转向半径作为R,同时可知前轮转向半径也为R;
注2:由于车速很慢,可以将后轮转向角视为0度,在后轮前进方向的垂直方向上选择转向圆心;取前轮前进方向的垂直方向与后轮前进方向的垂直方向的交点,作为真正的转向中心;
注3:轮胎的转弯半径
一般是远大于车辆的横向轴距
的;
- 可以认为左前轮和左后轮的转弯半径相同,均为
;
- 可以认为右前轮和右后轮的转弯半径也是相同的,均为
;
推导过程:
a
a
a
总结:
- 阿克曼转向几何重要公式:
- 阿克曼转向几何重要推论:车辆转角
越大,这外轮与内轮的转向角之差越大
- 补充1:转向的时候内侧轮转角大,外侧轮转角小
- 补充2:从阿克曼转向几何的公式可以看出,自行车模型更适合在转角
比较小的时候使用;因为我们要保证车辆模型可以简化为自行车模型用来分析,就要保证两侧轮胎的转角之差不能太大,如果转向比较剧烈,那么内外侧轮胎的转角之差会很大,就难以将两侧轮胎视为同一个轮胎进行简化
a
a
a
a
a
a
3.2 经典控制理论判断系统稳定性
3.2.1 经典控制理论判断控制系统的稳定性
注:系统的稳定性可以分为【内稳定性(李雅普诺夫稳定)】和【外稳定性(BIBO)】;经典控制理论所研究的则是外稳定,而现代控制理论所研究的则是内稳定;
关于控制系统稳定性的描述:如果一个系统受到扰动,偏离了原来的平衡状态,而当扰动消失以后,经过充分长的时间,这个系统又能够以一定的精度恢复到原来的状态,则称系统是稳定的,否则称这个系统是不稳定的;
a
a
举例1:如上图所示的摆,球初始位置是在M点,把它拉到b点放下,球在经过反复折腾后,还是会回到M点,所以这是一个稳定的系统,M点是稳定的平衡点;
a
a
举例2:如果所示的小球,a点是平衡点,因为在a点,受到有限的力后,球会回到a点。但是在b点,受到有限的力后,球回不到b点,则b点不是稳定的点;
线性定常系统稳定的充要条件:特征方程的根具有负实部(系统特征方程式的根就是该系统传递函数的闭环极点)
a
a
解释:因为传递函数的极点
在特征方程中对应的项就是
,只有当
的值小于0时,随着时间t的增大,项
才会不断减小直至为0,这样系统才没有了波动,系统可以收敛到稳定状态;
a
a
注1:所以控制系统稳定的充分必要条件也可说成是闭环传递函数的极点全部具有负实部或者说闭环传递函数的极点全部在s平面的左半平面;
a
注2:但是由于控制系统的微分方程如果是高阶的,那么将特别难解出其根,为了避开解方程,提出了很多可以判断系统稳定性的方法(劳斯判据 / 赫尔维茨判据 / 奈奎斯特判据 / 通过伯德图判断 .... 各种各样的方法);
3.2.2 外稳定的局限性
注1:我们上面提到的通过判断传递函数所有极点的实部是否为负,来判断系统稳定性的方法,判断的就是系统的外稳定性(BIBO);
注2:外稳定具有局限性,因为需要前提条件 -- 系统的初始状态为0;否则一个系统将无法达到外稳定;
说明:
a
该控制系统的极点有两个,一个大于0一个小于0,但是通过对零极点的对消,可以使得系统的传递函数只含有一个小于0的极点,因而系统达到外稳定;
a
a
将传递函数转换为系统特征方程:
a
a
我们发现:如果系统的初始条件不为0,那么系统的
和
项会一直发散,使得系统无法达到稳定状态,所以我们如果想判断系统的外稳定性,就一定要保证系统的初始条件为0;
3.2.3 经典控制理论和经典控制理论的差别
- 关于系统内部状态:
- 经典控制只关心系统的输入与输出,不关心系统运行时的内部状态;从传递函数就可以看出经典控制理论是直接求解“输出 / 输入”的频域表达式,旨在通过输入直接调控输出,关于调控过程中系统的其他状态量毫不关心;
- 而现代控制不仅关注系统的输入输出,还关心系统的内部状态;现代控制理论旨在在使用一阶线性微分方程建立时域表达式,其中的状态量就是系统的各个内部状态的具体表现;
- 关于使用场景:
- 经典控制系统一般局限于单输入单输出、线性定常系统;
- 现代控制理论不仅适用于单输入单输出系统,还可以研究多输入多输出系统;不仅可以分析线性系统,还可以分析非线性系统;不仅可以分析定常系统,还可以分析时变系统;
- 分析方法:
- 经典控制理论主要采用频域分析;
- 现代控制理论主要使用时域分析;
a
a
a
a
a
a
3.3 现代控制理论判断系统稳定性
3.3.1 如何建立状态空间方程
参考视频:【Advanced控制理论】2_状态空间_State Space_哔哩哔哩_bilibili
传递函数和状态空间方程之间的联系:(初始条件为0)
3.3.2 如何判断系统的稳定性
- 如果矩阵
的所有特征值均为负,则该系统是内稳定的;
- 如果传递函数
的所有极点的实部均为负,则该系统是外稳定的;
注意:
- 如果一个系统内稳定,那么他一定外稳定(因为传递函数最差的结果就是没有零极点对消,即传递函数
的所有极点就是矩阵
的所有特征值)
- 如果一个系统外稳定,并不能推出该系统也是内稳定的(因为外稳定很可能是因为零极点对消导致的,矩阵
仍是存在正值的特征值的)
举例:系统是外稳定的,但是不是内稳定的;
3.3.3 系统的能控性和能观性
系统的能控性:对于一个线性定常系统,如果均存在一个输入,对于任意一个状态
的任意时刻的值
,在有限的时间内,可以使状态
到达任意的其他值
,那么我们称这个系统是可控的,否则就是不可控的;(注意是这个系统涉及到的所有的状态变量都是可控的,这个系统才是可控的)
a
a
如何判断系统的能控性:矩阵
是行满秩的;
系统的能观性:对于一个线性定常系统,任何一个状态变量
的初始值
,均可以通过在有限时间内对输入
和输出
的观测,从而推导出来,则称这个系统是能观的;
a
a
如何判断系统的能观性:矩阵
是列满秩的;
a
a
为什么需要判断系统的能观性:因为在实际的应用中很多的系统状态并不能通过直观的测量而得到的,而是需要通过我们观测的值反推计算得到的;
a
a
a
a
a
a
3.4 基于车辆几何模型的横向控制
注:主流的横向控制方法主要有两类,一种是基于几何的方法,另一种是基于模型的方法;
3.4.1 纯追踪法(Pure Pursuit)
注1:纯追踪法(Pure Pursuit)是一种基于几何的追踪方法;
注2:纯追踪法在低速状态下有很好的效果(是因为该方法是基于自行车模型推导出来的,而自行车模型的应用有两个前提 -- 低速+小转向角),他是基于自行车模型和阿克曼转向几何推导出的算法;
回顾阿克曼转向几何:通过阿克曼转向几何,我们可以得到前轮转角
和后轮转弯半径
之间的关系;
a
a
补充:我在上面的推导过程中得到的公式是
而不是
,不过其实这俩公式用哪个都可以;区别仅在于推导过程中对
的处理,不过因为转向角很小的缘故,不管是将
保留还是将其约等于为
都是可以的;
a
a
a
纯追踪法的使用步骤:
- 通过GPS确定车辆的当前位置
- 找到规划的目标路径path中和车辆当前位置距离最近的点(waypoint)
- 以该点为圆心,前视距离
为半径,找出和目标路径path的交点,作为车辆的目标点G(go_point)
- 将目标点G转化到车辆坐标系中,方便进行跟踪
- 通过公式计算车辆的转向角
,并操纵车辆的转向运动
- 隔一段时间更新一次车辆位置和状态
a
a
纯追踪法的目的:以后轮为基点,车的纵向车身为切线,通过控制前轮转角,使得车辆可以沿着一条通过目标点的圆弧行驶;(通过几何关系,仅凭车辆当前位置和获得的下一个目标点G的位置,就可以计算出车辆所需的转向角
)
a
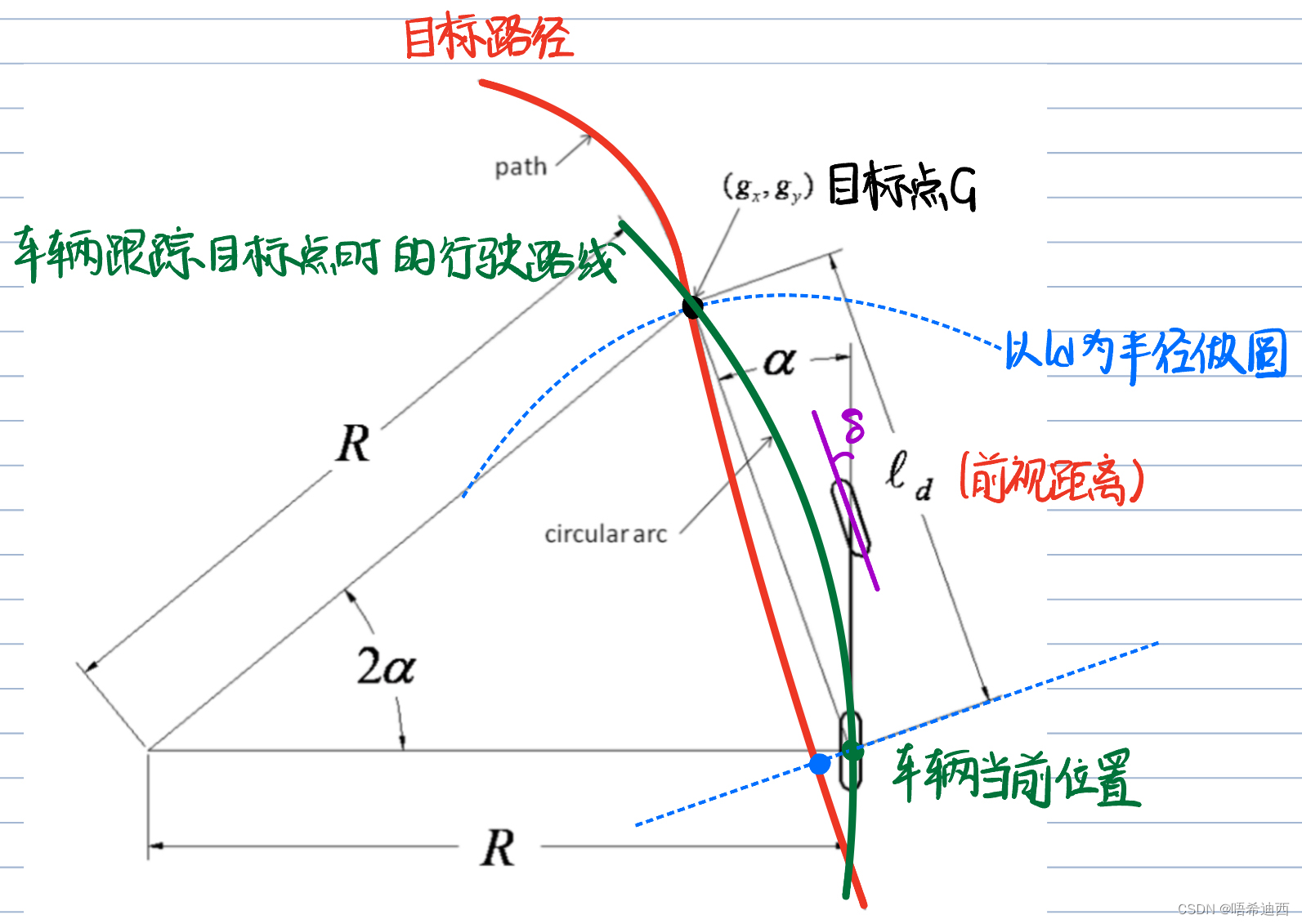
纯追踪法的推导过程:
a
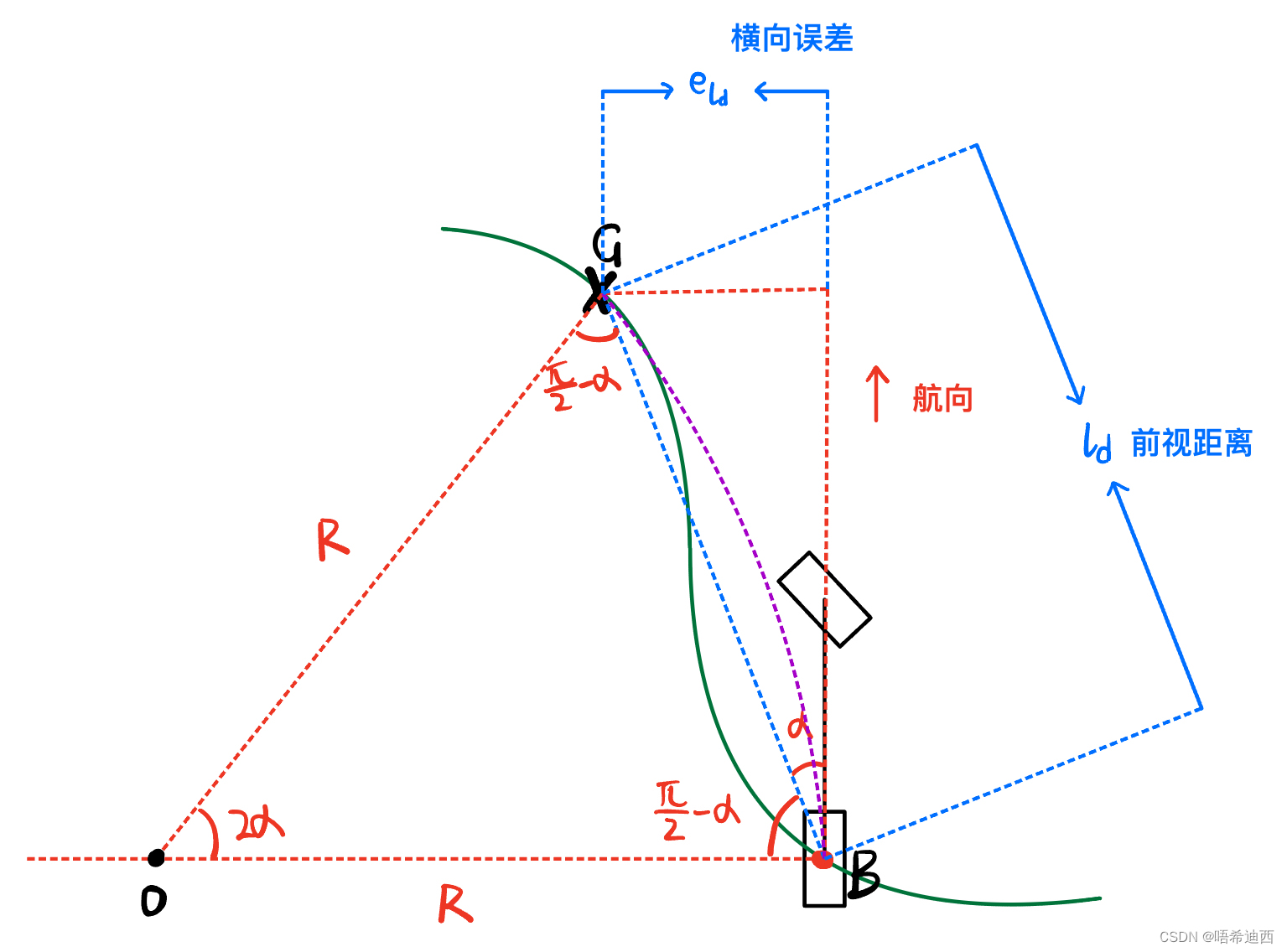
(1)通过几何作图确定目标点G以及转弯半径R:找到目标点G以后,我们可知当前车辆航向和目标点之间的夹角
的大小;同时因为我们的目的是沿一段圆弧走到目标点G,所以OGB是一个等腰三角形,底角的大小为
;通过作图可知车辆的转弯半径为R;
a
(2)在三角形OGB中使用正弦定理:通过几何关系求出车辆转向角
和其他已知信息之间的关系;(公式中的
的含义是:因为车辆一直处在行进阶段,到达一个目标点后就会求出下一个目标点,那么夹角
的值是跟随时间的变化在不断变化的,因此公式中用
代替;同理
)
a
(3)总结:纯跟踪法的转向角计算公式(下面两个都可以);
a
纯跟踪法的缺点:由公式我们可知,影响纯追踪法的性能中最重要的因素是
;这个量会直接影响到我们计算的车轮转角的大小,从而影响车辆对轨迹的追踪能力;
- 如果
较小,我们跟踪车辆轨迹的效果会更好,但是由于会经常更换目标点,会导致系统的稳定性会降低;
- 如果
较大,我们在跟踪车辆轨迹的过程中系统表现的会更稳定,一直沿着一个圆弧行驶,但是对轨迹跟踪的准确性会降低;
纯跟踪算法可以看做是以车辆后轴中心相对于预瞄点的横向位置误差比例控制器,而比例控制器决定了控制品质上限不高;
跟踪算法可以缩小车辆与期望轨迹的位置偏差,但是对角度偏差束手无策,因为数学原理上根本就没有考虑角度偏差(纯跟踪法的目的只是令车辆后轮到达指定目标点即可,但是对车辆的朝向没有要求);
要求轨迹多帧连续性好,因预瞄的特性无法对变化轨迹(尤其是预瞄距离内)进行响应;
a
a
优化:
- 将
修改为
:随着速度增加
就可以越来越大,这样可以令纯跟踪法对不同速度的适应能力变强,但是k的值大小也会影响系统的稳定性/跟踪的精确性;
- 对
附加一个取值范围
:确保
的值不会太小也不会太大;
纯跟踪法的优点:通过纯跟踪法的公式可以看出,公式中没有涉及到目标路径path的相关信息(如曲率等...),说明这个方法对局部规划出的目标路径的连续性要求不高,所以纯跟踪法可以很好的处理不连续的轨迹跟踪问题;
3.4.2 斯坦利控制(Stanley Controller)
注:斯坦利控制(Stanley Controller)和纯追踪法一样,都是一种基于几何的轨迹追踪方法;
注1:斯坦利控制和纯追踪法之间的不同点
- 纯追踪法的参考点选择的是后轮中心;而斯坦利控制选取前轮中心为参考点;
- 纯追踪法需要前视距离
来协助画圆找出目标点G的位置;而斯坦利控制可以直接通过匹配最近的waypoint的方法就可以获得目标点G的位置;
- 纯追踪控制的横向误差
需要通过
求出,即需要借助
才行;但是斯坦利控制只需要直接计算车辆当前位置和匹配的waypoint之间的距离即可,这个距离就是横向误差
;
- 斯坦利控制对于偏差的补偿是相对独立的;而纯追踪控制则是将所有的补偿全部合在一起输出的;
a
a
注2:斯坦利控制器的三个组成部分
- 对导航角误差(heading error)的矫正 --
;
- 对横向误差
(position error / cross error)的矫正 --
;
- 对前轮转角
的范围限制 --
;
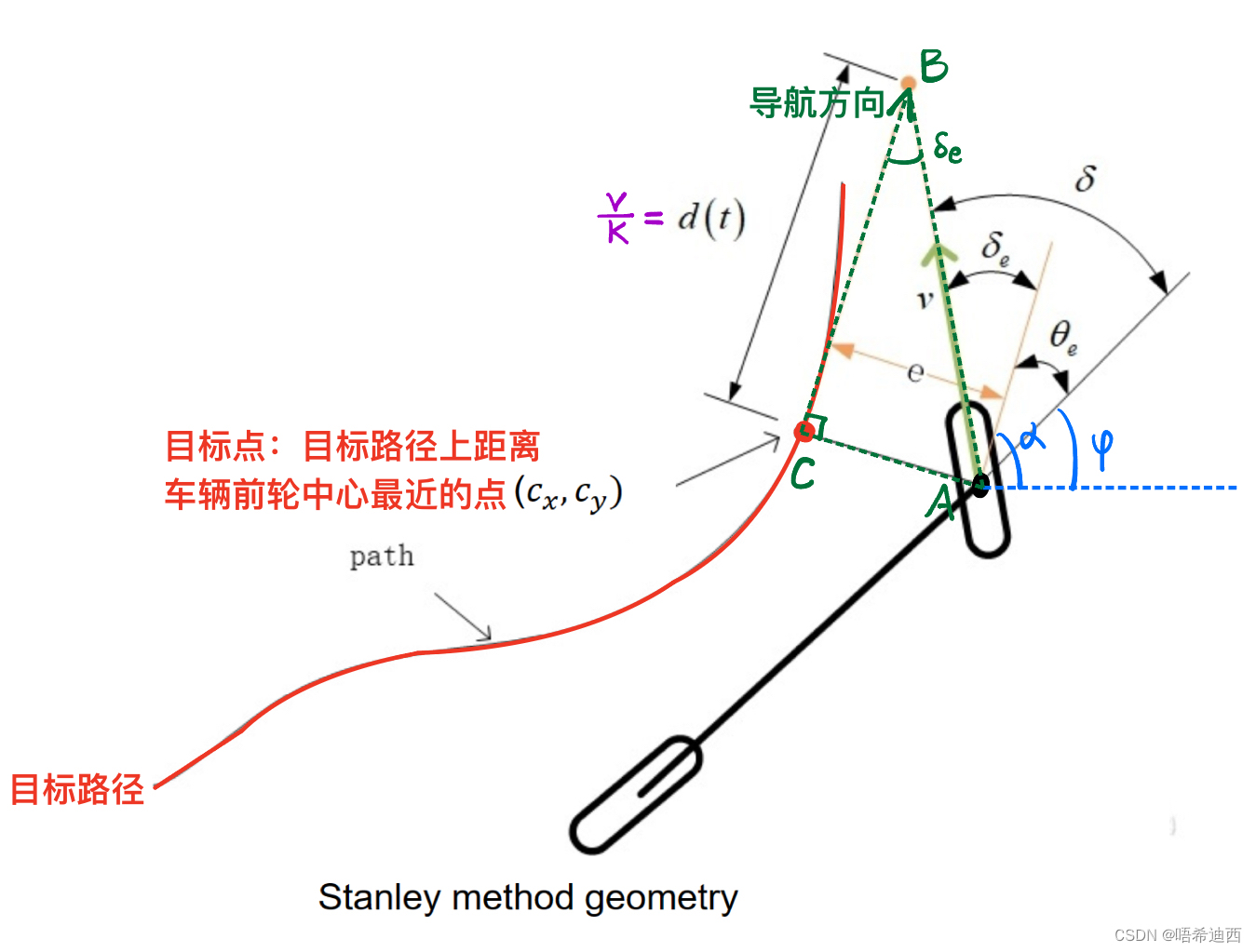
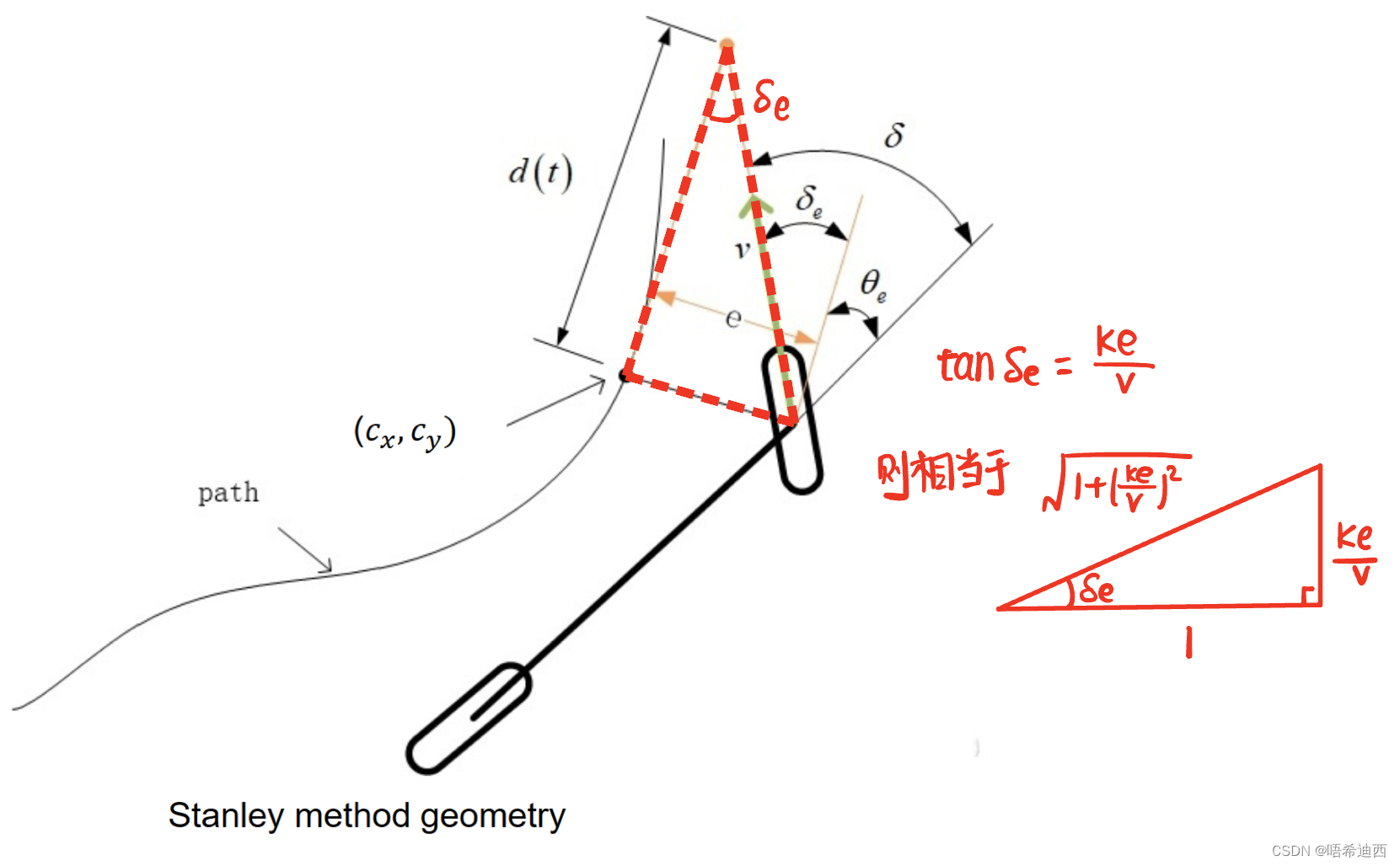
斯坦利控制器推导:
:目标点处的切线方向,即导航方向
:车辆横摆角(低速情况下与车辆的行驶方向相等,即车纵轴指向方向即为车辆真实的行驶方向)
:前轮转角,范围在
之间
:导航角误差(heading error),大小为车辆真实的行驶方向(横摆角)和参考点指定的导航方向(参考点的切线方向)之间的差角,正负在下面另有介绍
:横向误差,大小为车辆前轮中心和参考点之间距离的平方,正负在下面另有介绍
:相当于斯坦利控制中的前视距离(k值是可以根据实验场景的不同来进行调整的)
:横向误差
所造成的转角大小,大小为前轮应当转过的角度
与导航方向之间的夹角,正负则与公式中的横向误差
的正负有关
a
a
斯坦利控制器的最终表达形式(三部分组成):
a
a
总结:斯坦利控制其实就是三部分组成的,分别对不同类型的偏差做出对应的补偿行为;
- 对导航误差的补偿
;
- 对横向误差的补偿
;
- 对前轮转角大小的限制
;
a
补充1:关于车辆前轮转角
的方向问题
a
a
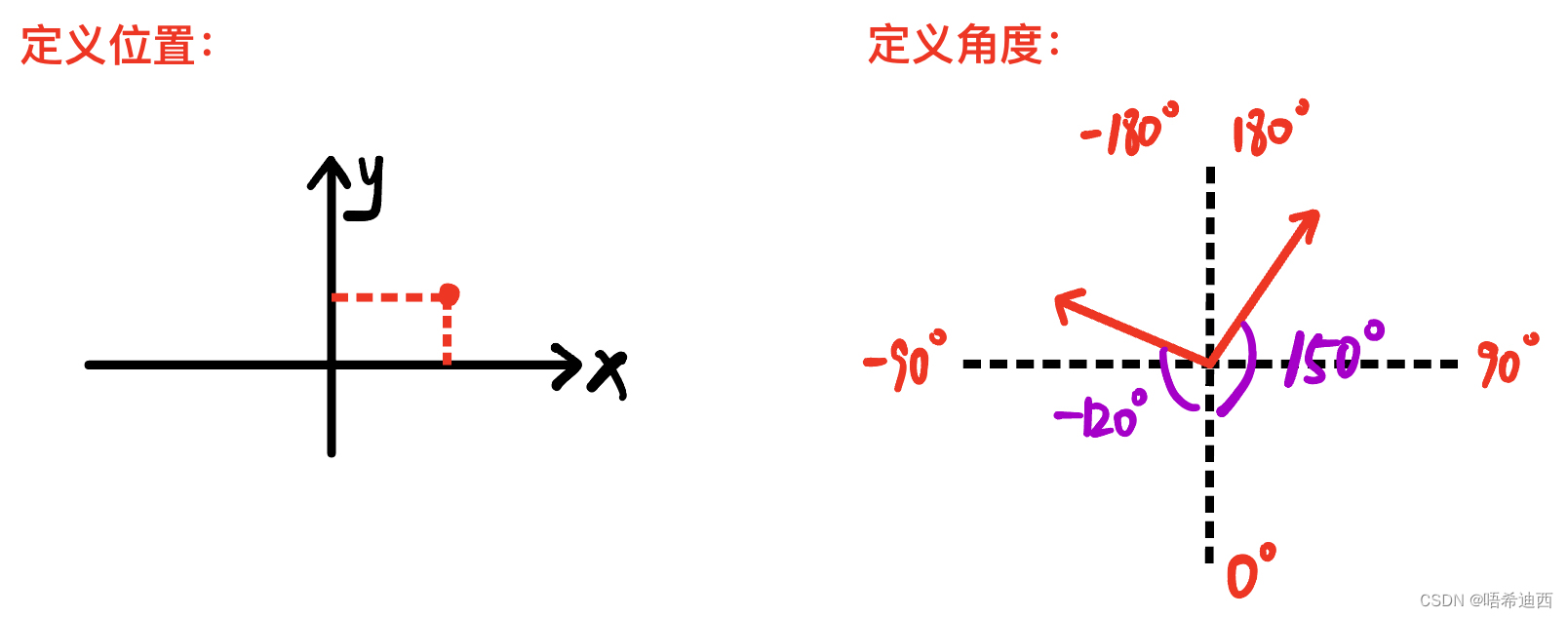
注意:在使用公式进行计算时,我们默认是在全局坐标系下进行的,而全局坐标系是如下图这样定义位置和角度的
a
a
在全局坐标系中:(下面的所有计算和分析都以这个为准)
:左打方向盘
:右打方向盘
a
a
在Carla模拟器中:(如果需要将我们在全局坐标系中计算得出的
和
赋值给模拟器,那就要给他们加上负号,再传递给Carla模拟器)
:右打方向盘
:左打方向盘
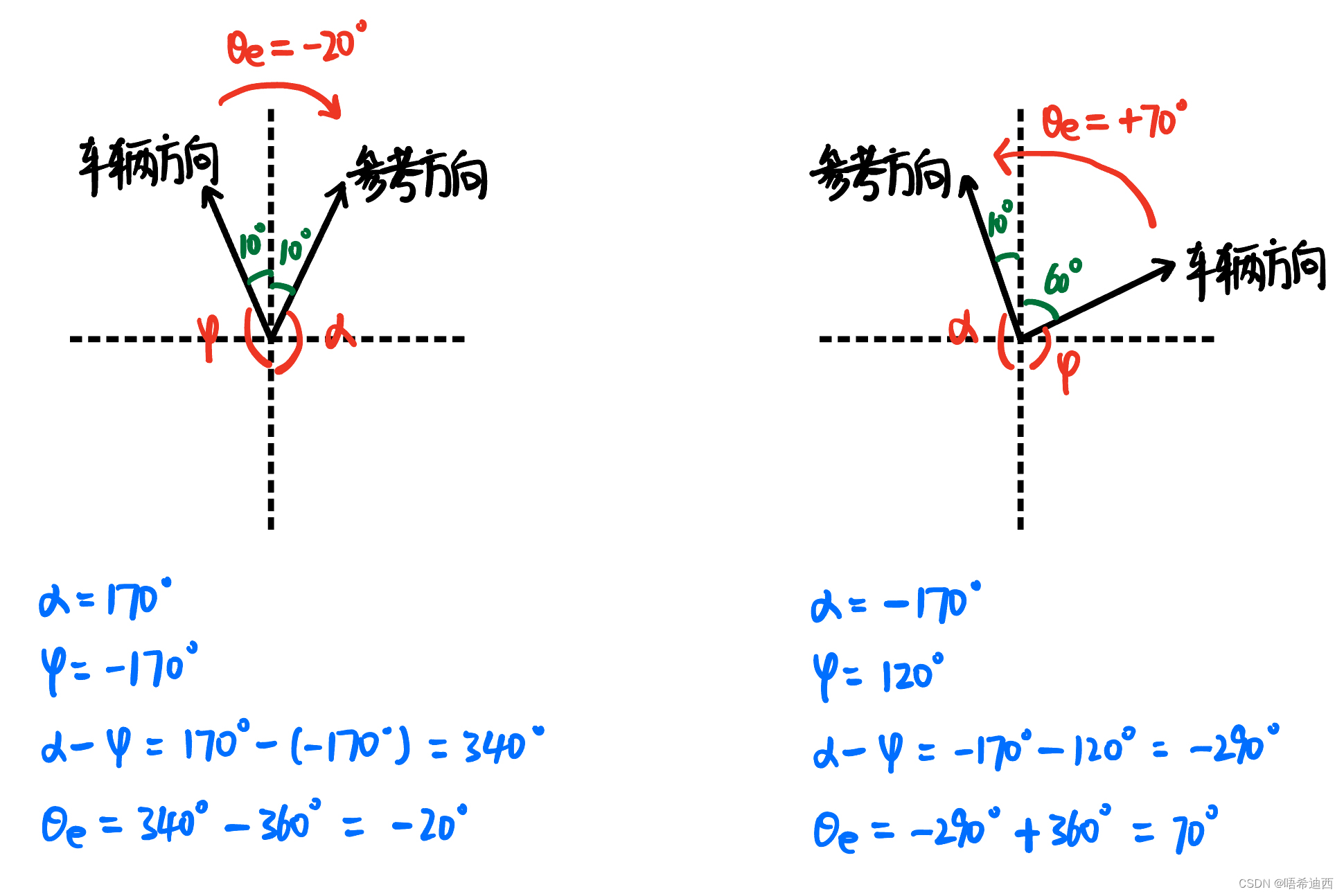
补充2:关于导航角误差
的正负问题
- 注意1:导航角误差的计算公式为
;
- 注意2:导航角误差需要控制在
的区间内;
- 注意3:从车辆状态中读取到的角度都是弧度,同理给Carla模拟器传递值的时候也要传递弧度;
a
a
举例:(在全局坐标系中计算)
a
a
代码示例:
e_theta = nearest_point.heading - theta; //nearest_point.heading:导航角 //theta:车辆朝向角 //将导航角限制到[-pai, pai] if(e_theta > M_PI) e_theta = e_theta - 2 * M_PI; else if(e_theta < -1 * M_PI) e_theta = e_theta + 2 * M_PI; //因为Carla中的方向和全局坐标系的方向相反 e_theta *= -1;
补充3:关于横向误差
的正负问题
- 横向误差的大小:为参考点与车辆前轮中心之间距离的平方;不过我们在实际写代码的时候,使用的是参考点与车辆质心之间距离的平方,因为我们获得的车辆的位置信息(x, y)都是车辆质心在全局坐标系下的坐标;
- 横向误差的正负:不能使用全局坐标系来判断横向误差
的正负,而需要使用车身坐标系来判断;
a
a
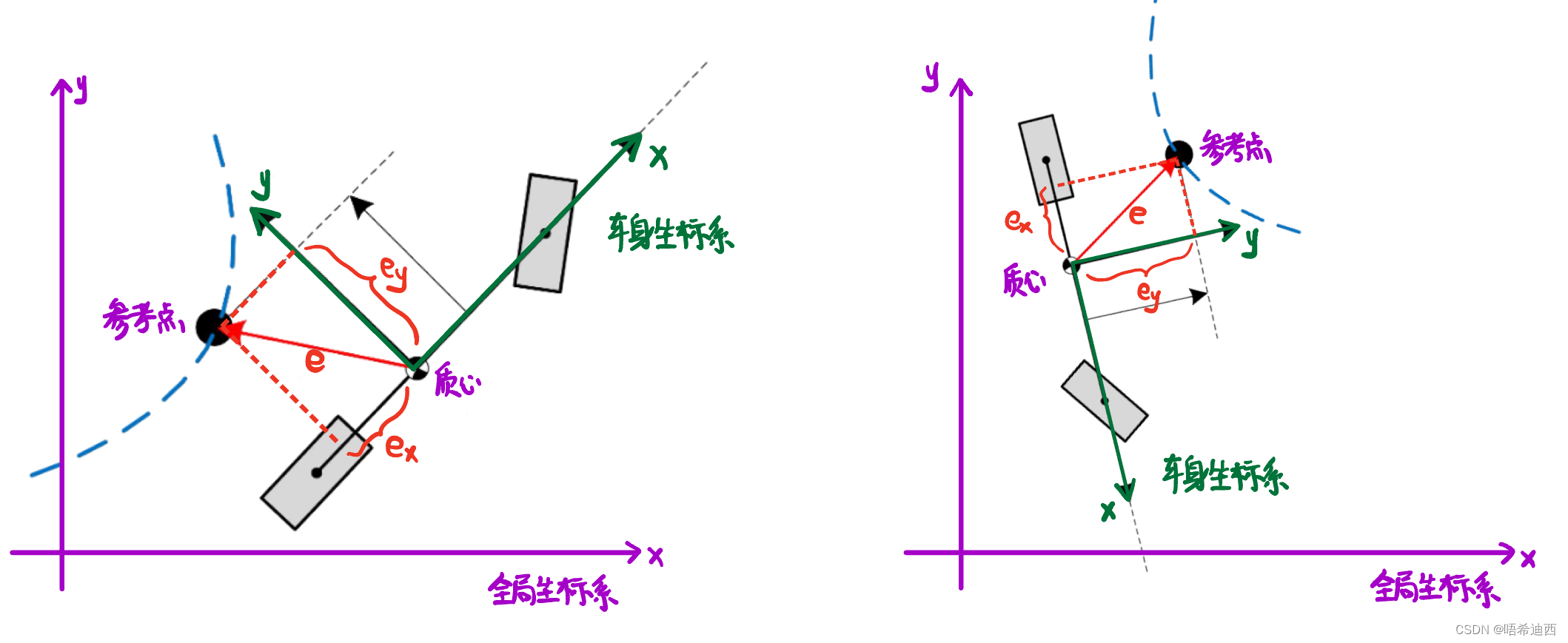
分析1:不能使用全局坐标系判断
的正负,而应该用车辆坐标系来判断,如下两种情况,这两种情况的导航角误差
为0,也就是说前轮转角只由横向误差导致的
决定,即
;
- 如果使用全局坐标系判断正负:第1种情况在全局坐标系下,横向误差
为正(假设
为“质心位置x坐标 - 参考点x坐标”);而第2种情况在全局坐标系下,横向误差
为负;但是由于车辆的行进趋势是要往减小横向误差
的方向进行的,所以这两种情况得到的
虽然正负不同,可是车辆却都要左转,即
,所以不能使用全局坐标系判断横向误差
的正负;
- 如果使用车身坐标系判断正负:判断
的正负,需要借助横向误差
在车身坐标系的
轴上的分量
的正负;因为借助车身坐标系,参考点的位置相对于车身的位置是固定的,那么
的正负就是固定的;
a
a
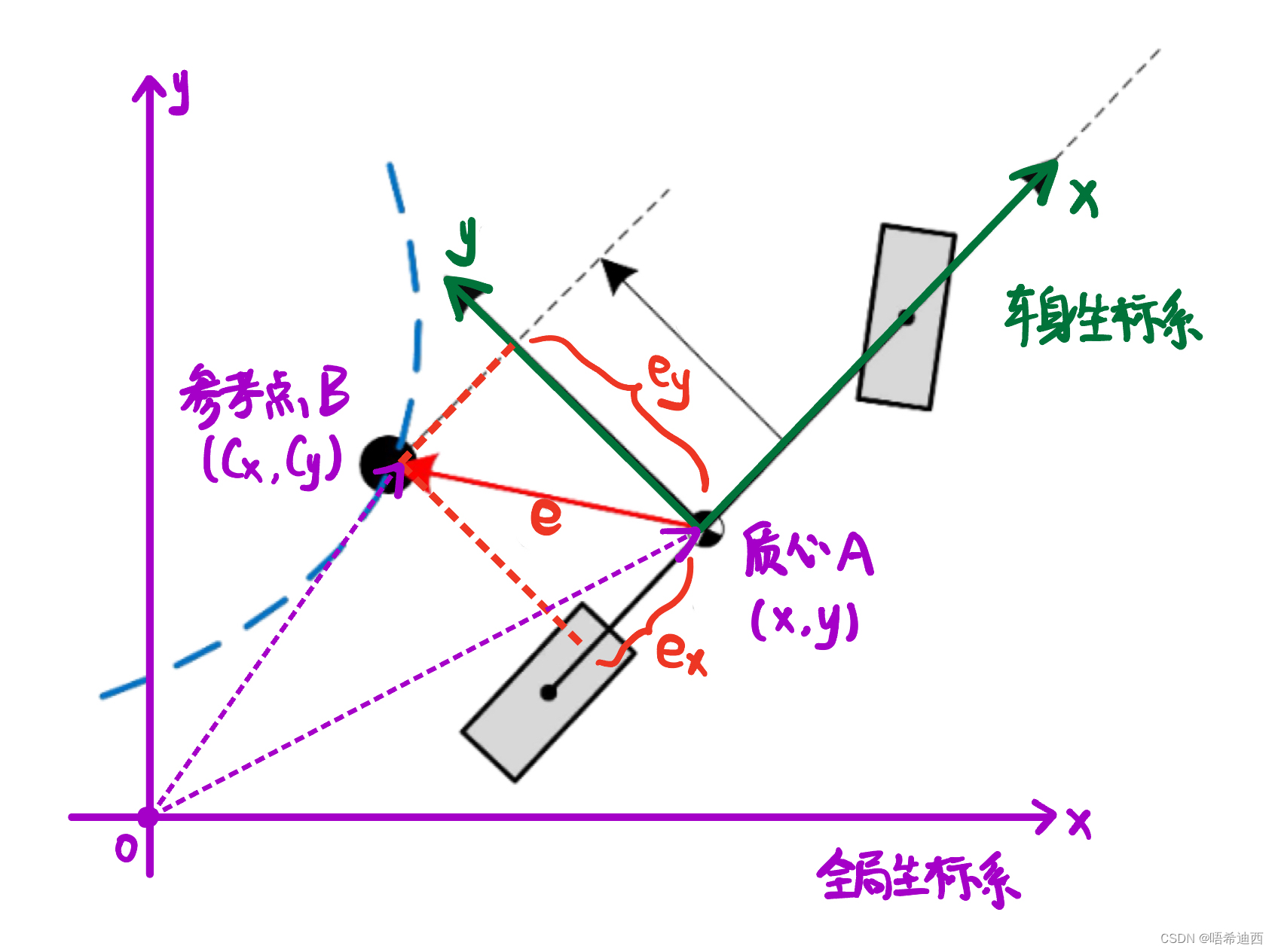
分析2:关于横向误差
的定义,大小和方向
- 定义:全局坐标系下定义为【参考点向量 - 质心向量】
- 大小:在全局坐标系下计算
- 方向:在车身坐标系下计算
为正或为0,则
为正;
为负,则
为负;
a
a
分析3:如何求
的值?我们求出来的横向误差
是全局坐标系中的向量,而我们要求的
则是向量
在车身坐标系中的
轴上的分量;如果我们想求
,则需要求出车身坐标系中横向误差
的表达式;
注意:车身坐标系的xyz轴由右手定则确定
- 大拇指x,食指y,中指z
- 其中x轴指向车辆的纵轴方向,即车辆的前进方向
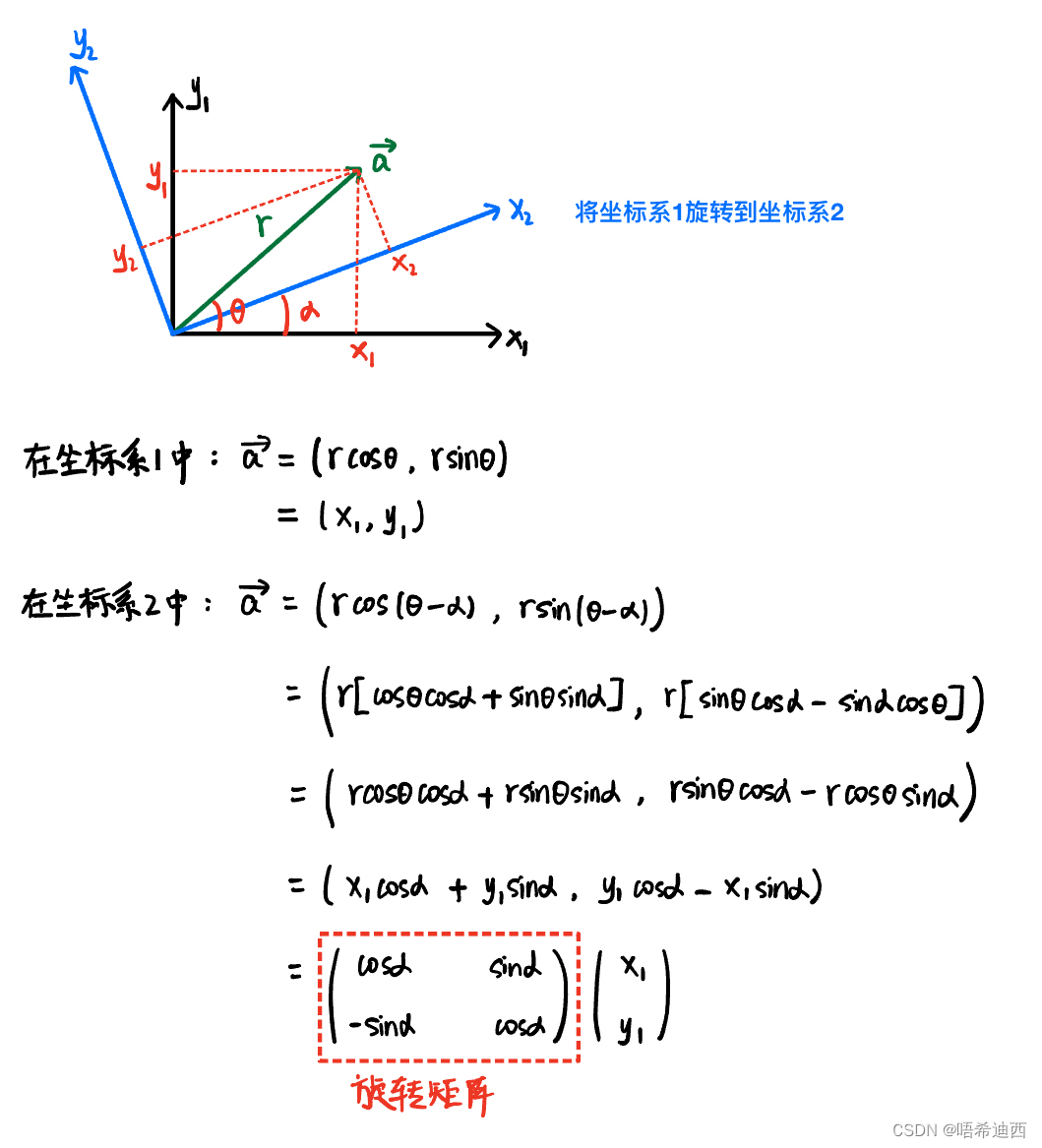
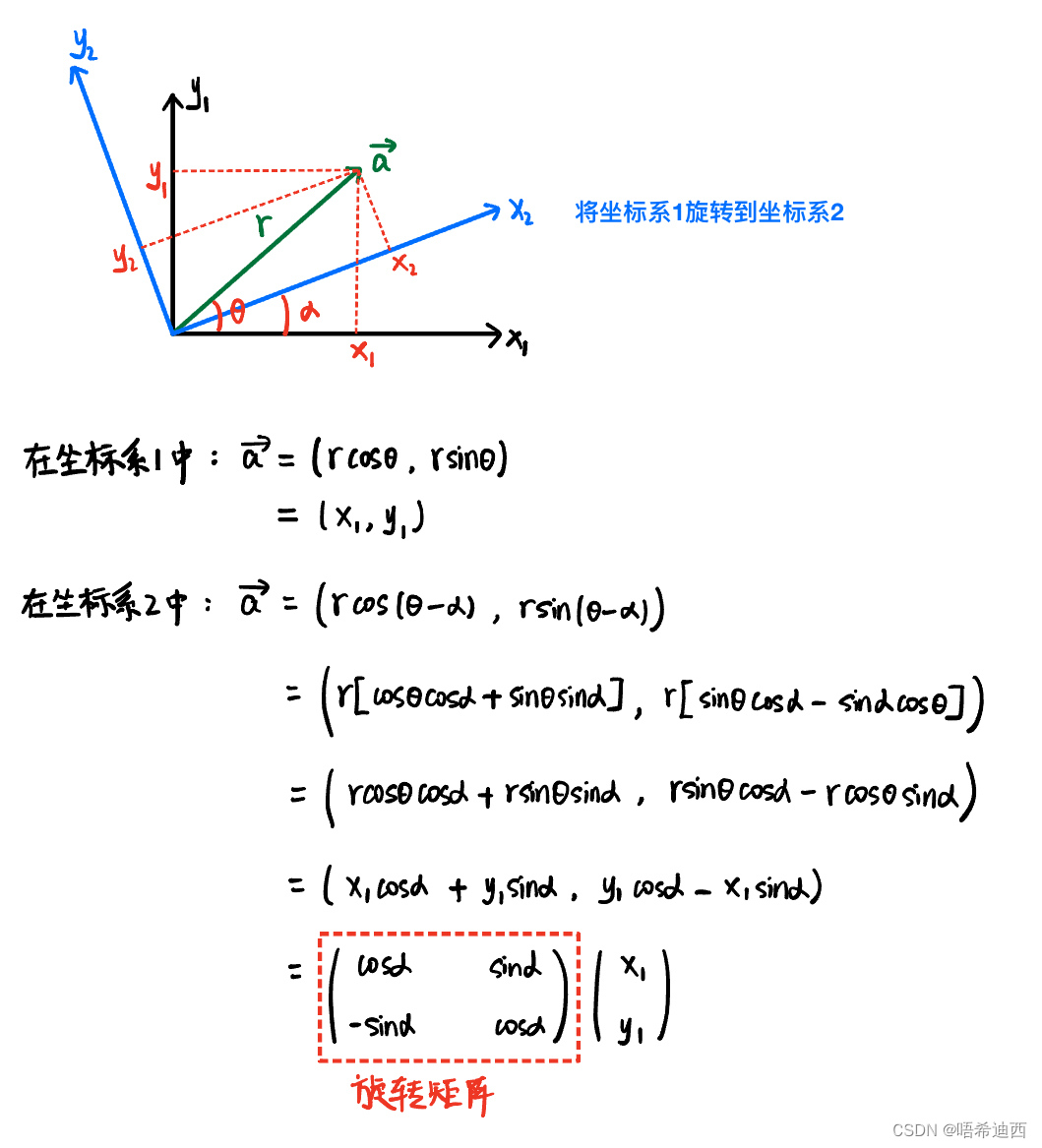
补充:全局坐标系 --> 车身坐标系的旋转矩阵
分析4:计算
的公式为
a
a
总结:(其中的角
即为车辆的朝向角)
- 横向误差的大小:
- 横向误差的方向:
a
a
代码:
//计算横向误差的大小 e_y = dy * dy + dx * dx; //判断横向误差的正负 //注意:后面if判断以后加负号是因为Carla中的方向和全局中的方向是相反的 double judge_e_y = 0; judge_e_y = dy * cos(theta) - dx * sin(theta); if(judge_e_y > 0) e_y = -1 * e_y; else if(judge_e_y < 0) e_y = e_y;
a
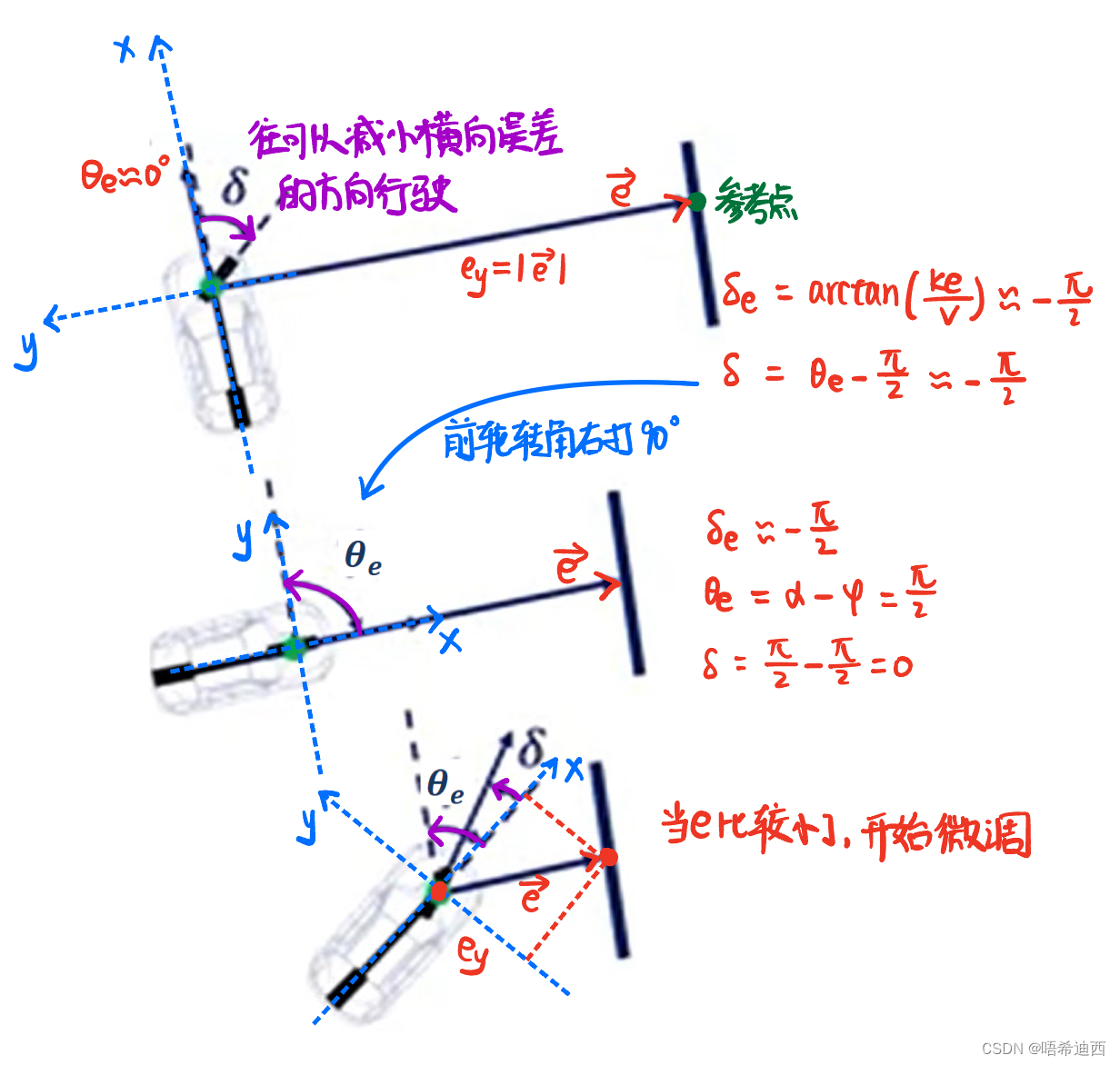
举例1:导航角误差很大时
a
a
举例2:横向误差很大时
a
斯坦利控制的稳定性分析:(针对其横向误差
的变化率进行分析)
a
a
注:直接将横向误差的变化率定义为
- 即直接用车速在横向上的分量表示横向误差的变化率;
- 由于横向误差是随着时间减小的,所以其变化率为负数;
a
a
推导过程:
当横向误差比较小的时候,可以将横向误差变化率的分母视为1,简化公式为:
- 类似于指数衰减,因此是一个稳定的过程;
- K值越大,横向误差的衰减越快;
a
对斯坦利控制器的改进:
(1)针对噪声:在原始斯坦利控制器的横向误差补偿项
的分母上,只有车辆的速度;如果对车辆的速度的测量结果被引入了很大的噪声,那么会导致
的剧烈波动;我们的改进措施为在分母上加上一个常数
;
(2)高速情况:在高速的情况下,直接将导航角误差
求出然后赋值给
,会导致车辆迅速发生偏转,毕竟速度太大了,一打方向盘车就歪这走了很远,所以这样的控制策略针对告诉情况有些激进;我们的改进方法为在求导航角误差
时,在其前面加一个阻尼项(一个PD控制器),以确保高速情况下
可以更缓慢和准确的变化;
(3)几何:纯跟踪法和斯坦利控制都有这个缺陷,因为他们都是根据几何关系推导得到的,而并没有考虑过参考路径(reference path)的曲率等因素;改进方法为引入一个前馈项(直接将曲率前馈即可)来提高车辆跟踪轨迹的能力;
a
a
总结所有的改进:
3.4.3 斯坦利控制代码完整版
头文件定义1:
//注意:存储车辆当前状态的所有信息
struct VehicleState {
double x;
double y;
double heading; //车辆朝向
double kappa; //曲率(切线斜率)
double velocity; //速度
double angular_velocity; //角速度
double acceleration; //加速度
// 规划起点
double planning_init_x;
double planning_init_y;
double roll;
double pitch;
double yaw;
double target_curv; //期望点的曲率
double vx;
double vy;
double vz;
double v;
// added
double start_point_x;
double start_point_y;
double relative_x = 0;
double relative_y = 0;
double relative_distance = 0;
double start_heading;
};
//注意:存储某一个轨迹点的所有信息
struct TrajectoryPoint {
double x;
double y;
double heading; //导航角
double kappa;
double v;
double a;
};
//注意:存储所有的参考轨迹点(即将目标路径上的所有轨迹点都存储下来)
struct TrajectoryData {
std::vector<TrajectoryPoint> trajectory_points;
};
//注意:要发送给Carla模拟平台,对Carla中建模的车辆进行控制的信息
struct ControlCmd {
double steer_target; //前轮转角(横向)
double acc; //加速度(纵向)
};头文件定义2:
class StanleyController {
public:
StanleyController(){};
~StanleyController(){};
void LoadControlConf();
void ComputeControlCmd(const VehicleState &vehicle_state, const TrajectoryData
&planning_published_trajectory, ControlCmd &cmd);
void ComputeLateralErrors(const double x, const double y, const double theta, double &e_y, double &e_theta);
TrajectoryPoint QueryNearestPointByPosition(const double x, const double y);
protected:
std::vector<TrajectoryPoint> trajectory_points_;
double k_y_ = 0.0;
double u_min_ = 0.0;
double u_max_ = 100.0;
double theta_ref_;
double theta_0_;
};主文件:
//PID控制器中的微分环节相当于阻尼,加在航向误差引起的前轮转角上
shenlan::control::PIDController e_theta_pid_controller(1.0, 0.0, 0.4);
//注意:arctan计算出来的是角度,这个函数的作用是将角度变换为弧度
double atan2_to_PI(const double atan2) {
return atan2 * M_PI / 180;
}
//注意:函数作用是返回车辆本身坐标(x, y)和目标点point之间的距离的平方
double PointDistanceSquare(const TrajectoryPoint &point, const double x, const double y) {
const double dx = point.x - x;
const double dy = point.y - y;
return dx * dx + dy * dy;
}
//注意:函数作用是定义参数k,即计算横向误差引起的转向角时要用到的参数k
void StanleyController::LoadControlConf() {
k_y_ = 0.5;
}
///** to-do **/ 计算需要的控制命令, 实现对应的stanley模型,并将获得的控制命令传递给汽车
//提示1:在该函数中你需要调用计算误差
//提示2:控制器中前轮转角的命令是弧度单位,发送给carla的横向控制指令范围是(-1~1)
void StanleyController::ComputeControlCmd(const VehicleState &vehicle_state, const TrajectoryData &planning_published_trajectory, ControlCmd &cmd) {
//(1)Caluate e_y, e_theta(计算横向误差和航向角误差)
trajectory_points_ = planning_published_trajectory.trajectory_points;
double e_y = 0; //横向误差
double e_theta = 0; //航向角误差
ComputeLateralErrors(vehicle_state.x, vehicle_state.y, vehicle_state.heading, e_y, e_theta);
//(2)Caluate delta_e(横向误差带来的转角)
double ks = 1.1; //增大该值系统的震动减小(变得更稳定),但车辆转弯角度减小,导致转弯缓慢;
double velocity_ = vehicle_state.velocity;
double delta_e = atan2( k_y_ * e_y , ks + velocity_ );
//(3)Limit the angle(给航向角误差加一个PD限制器)
double e_theta_pd = e_theta_pid_controller.Control(e_theta, 0.01);
//限制横向误差带来的转角的范围
if(delta_e > M_PI) delta_e = delta_e - 2 * M_PI;
else if(delta_e < -1 * M_PI) delta_e = delta_e + 2 * M_PI;
//限制航向角误差的范围
if(e_theta_pd > M_PI) e_theta_pd = e_theta_pd - 2 * M_PI;
else if(e_theta_pd < -1 * M_PI) e_theta_pd = e_theta_pd + 2 * M_PI;
//(4)Import feedback(在斯坦利控制中引入前馈项)
TrajectoryPoint nearest_point = QueryNearestPointByPosition(vehicle_state.x, vehicle_state.y);
double kappa_ = 0; //曲率
double weight_kappa_ = 2.3; //前馈项为一个正比例函数,该项为其权重
if(isnan(kappa_)) kappa_ = 0;
else kappa_ = nearest_point.kappa;
double delta = e_theta_pd + delta_e + weight_kappa_ * kappa_;
//限制前轮转角的取值范围
if(delta > M_PI) delta = delta - 2 * M_PI;
else if(delta < -1 * M_PI) delta = delta + 2 * M_PI;
//限制前轮转角的机械转动范围
if(delta > atan2_to_PI(90.0)) delta = atan2_to_PI(90.0);
else if(delta < -1 * atan2_to_PI(90.0)) delta = -1 * atan2_to_PI(90.0);
std::cout << "e_theta_pd: " << (e_theta_pd / M_PI) * 180 << std::endl;
std::cout << "delta_e: " << (delta_e / M_PI) * 180 << std::endl;
std::cout << "delta: " << (delta / M_PI) * 180 << std::endl;
cmd.steer_target = delta;
}
///** to-do **/ 计算需要的误差,包括横向误差,朝向误差
//注意:误差计算函数没有传入主车速度,因此返回的位置误差就是误差,不是根据误差计算得到的前轮转角
void StanleyController::ComputeLateralErrors(const double x, const double y, const double theta, double &e_y, double &e_theta) {
TrajectoryPoint nearest_point = QueryNearestPointByPosition(x, y);
double dx = nearest_point.x - x;
double dy = nearest_point.y - y;
//计算横向误差的大小
e_y = dy * dy + dx * dx;
//判断横向误差的正负
//注意:后面if判断以后加负号是因为Carla中的方向和全局中的方向是相反的
double judge_e_y = 0;
judge_e_y = dy * cos(theta) - dx * sin(theta);
if(judge_e_y > 0) e_y = -1 * e_y;
else if(judge_e_y < 0) e_y = e_y;
//计算导航角误差
//注意:Carla中设置的是左打方向盘为负,右打方向盘为正,所以我们算出来的导航角误差应该乘-1
e_theta = -1 * (nearest_point.heading - theta);
//将导航角限制到[-pai, pai]
if(e_theta > M_PI) e_theta = e_theta - 2 * M_PI;
else if(e_theta < -1 * M_PI) e_theta = e_theta + 2 * M_PI;
std::cout << "e_theta: " << e_theta <<"\theading:"<< nearest_point.heading << "\ttheta :" << theta << std::endl;
}
//注意:返回参考路径上和车辆当前位置距离最近的waypoint(目标点),返回的是点结构体类型
TrajectoryPoint StanleyController::QueryNearestPointByPosition(const double x, const double y) {
double d_min = PointDistanceSquare(trajectory_points_.front(), x, y); //得到车辆当前位置距离参考路径的第一个点的距离
size_t index_min = 0; //当前waypoint在trajectory_points_中的索引下标
for (size_t i = 1; i < trajectory_points_.size(); ++i) {
double d_temp = PointDistanceSquare(trajectory_points_[i], x, y);
if (d_temp < d_min) {
d_min = d_temp;
index_min = i;
}
}
cout << " index_min: " << index_min << endl;
cout << "tarjectory.heading: " << trajectory_points_[index_min].heading << endl;
theta_ref_ = trajectory_points_[index_min].heading; //获得距离车辆当前位置最近的路径点的航向角
return trajectory_points_[index_min];
}









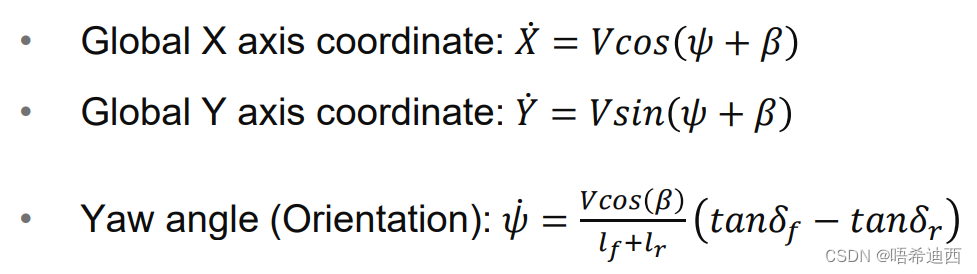
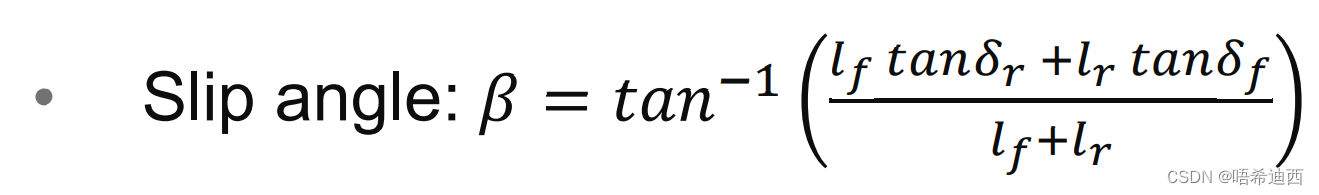












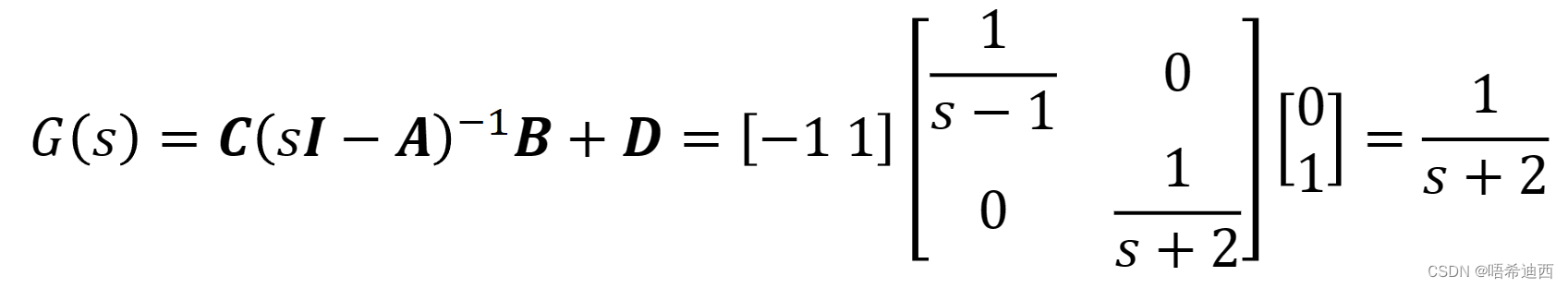




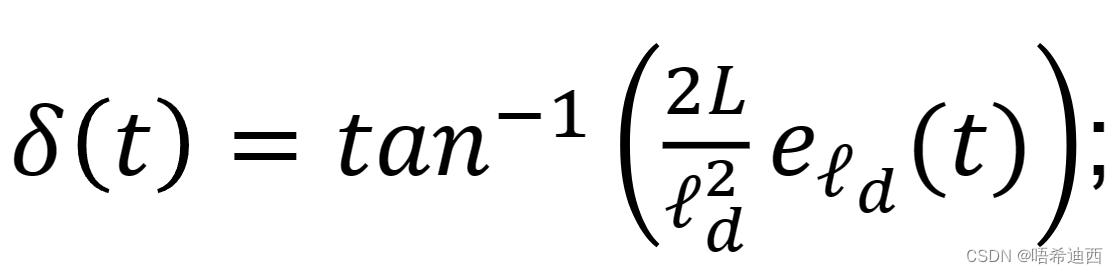







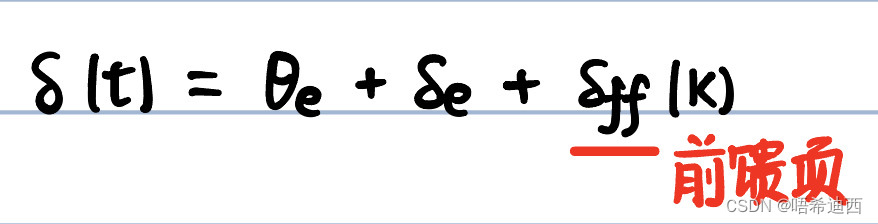


















 5180
5180

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








