一、函数正交性的定义
在数学分析中,正交的概念可以推广到连续函数上。如果函数 f ( x ) f(x) f(x) 和 g ( x ) g(x) g(x) 在某一区间 [ a , b ] [a, b] [a,b] 内正交,则有
∫ a b f ( x ) g ( x ) d x = 0 (1) \int_{a}^{b} f(x)g(x)dx = 0 \quad \tag{1} ∫abf(x)g(x)dx=0(1)
式 ( B . 1.6 ) (B.1.6) (B.1.6) 定义了函数之间正交的性质。我们将在此基础上进一步探讨三角函数的正交性。
二、三角函数系的定义
三角函数系是一个常见的正交函数集合,其形式为
{ 1 , sin x , cos x , sin 2 x , cos 2 x , sin 3 x , cos 3 x , ⋯ , sin n x , cos n x , ⋯ } (2) \{1, \sin x, \cos x, \sin 2x, \cos 2x, \sin 3x, \cos 3x, \cdots, \sin nx, \cos nx, \cdots\} \quad \tag{2} {1,sinx,cosx,sin2x,cos2x,sin3x,cos3x,⋯,sinnx,cosnx,⋯}(2)
这里的 1 1 1 可以理解为 cos 0 x \cos 0x cos0x。由于 sin 0 x = 0 \sin 0x = 0 sin0x=0,因此未包含在该集合中。三角函数系的正交性是指,在区间 x ∈ [ − π , π ] x \in [-\pi, \pi] x∈[−π,π] 内,该集合中的任意两个不同函数的乘积积分为零。
三、三角函数正交性的推导
以下是几种典型的三角函数正交性关系及其推导:
1. sin n x \sin nx sinnx 与 cos n x \cos nx cosnx 的正交性
根据三角函数的正交性定义,考虑 sin n x \sin nx sinnx 和 cos n x \cos nx cosnx 的乘积:
∫ − π π sin n x cos n x d x = 0 (3) \int_{-\pi}^{\pi} \sin nx \cos nx dx = 0 \quad \tag{3} ∫−ππsinnxcosnxdx=0(3)
利用三角函数的积化和差公式:
sin n x cos n x = 1 2 [ sin ( n + m ) x + sin ( n − m ) x ] \sin nx \cos nx = \frac{1}{2}[\sin(n+m)x + \sin(n-m)x] sinnxcosnx=21[sin(n+m)x+sin(n−m)x]
在区间 [ − π , π ] [-\pi, \pi] [−π,π] 内, sin ( n + m ) x \sin(n+m)x sin(n+m)x 和 sin ( n − m ) x \sin(n-m)x sin(n−m)x 的积分均为零,因为它们的积分值等于各自正弦函数的一个周期内的面积。
2. cos n x \cos nx cosnx 与 cos m x \cos mx cosmx 的正交性
对于 cos n x \cos nx cosnx 和 cos m x \cos mx cosmx(其中 n ≠ m n \neq m n=m),我们有:
∫ − π π cos n x cos m x d x = 0 (4) \int_{-\pi}^{\pi} \cos nx \cos mx dx = 0 \quad \tag{4} ∫−ππcosnxcosmxdx=0(4)
同样使用三角函数的积化公式:
cos n x cos m x = 1 2 [ cos ( n + m ) x + cos ( n − m ) x ] \cos nx \cos mx = \frac{1}{2}[\cos(n+m)x + \cos(n-m)x] cosnxcosmx=21[cos(n+m)x+cos(n−m)x]
在 [ − π , π ] [-\pi, \pi] [−π,π] 内, cos ( n + m ) x \cos(n+m)x cos(n+m)x 和 cos ( n − m ) x \cos(n-m)x cos(n−m)x 的积分分别为零。因此, cos n x \cos nx cosnx 与 cos m x \cos mx cosmx 在区间 [ − π , π ] [-\pi, \pi] [−π,π] 内正交。
3. sin m x \sin mx sinmx 与 1 1 1 的正交性
考虑 sin m x \sin mx sinmx 与 1 1 1 的乘积:
∫ − π π sin m x d x = ∫ − π π 1 ⋅ sin m x d x = 0 (5) \int_{-\pi}^{\pi} \sin mx dx = \int_{-\pi}^{\pi} 1 \cdot \sin mx dx = 0 \quad \tag{5} ∫−ππsinmxdx=∫−ππ1⋅sinmxdx=0(5)
由于 sin m x \sin mx sinmx 在 [ − π , π ] [-\pi, \pi] [−π,π] 内的积分是一个完整周期的正弦函数,其正负面积相互抵消,故积分结果为零。
四、正交性的几何意义
函数正交性在几何上可以理解为两个函数在函数空间中的正交投影。在物理学和工程学中,正交函数系常用于信号分解、傅里叶分析等领域。三角函数系作为一种经典的正交函数系,其重要性主要体现在以下方面:
- 傅里叶级数展开:任意一个满足一定条件的周期函数都可以表示为三角函数系的线性组合。
- 信号处理:正交函数系能够有效分解和还原信号,使得信号的分析更加简洁。
- 数值计算:正交性可以简化积分和计算,提高计算效率。
五、MATLAB可视化正交过程
以下是生成动态展示三角函数正交性积分过程的MATLAB代码:
% 参数设置
x = linspace(-pi, pi, 1000);
n = 3; m = 2; % 三角函数系数
sin_nx = sin(n*x);
cos_mx = cos(m*x);
product = sin_nx .* cos_mx; % 函数乘积
cumulative_integral = cumtrapz(x, product); % 预计算累积积分
% 创建动图
figure('Position', [100 100 800 800]);
step = 10; % 帧间隔(控制动图速度)
filename = 'orthogonal_integral.gif';
for i = 1:step:length(x)
% 绘制三个子图
% 1. 正弦函数
subplot(3,1,1);
plot(x, sin_nx, 'r', 'LineWidth', 1.5);
title(['sin(', num2str(n), 'x)']);
xlim([-pi pi]); grid on;
% 2. 余弦函数
subplot(3,1,2);
plot(x, cos_mx, 'b', 'LineWidth', 1.5);
title(['cos(', num2str(m), 'x)']);
xlim([-pi pi]); grid on;
% 3. 乘积及积分过程
subplot(3,1,3);
plot(x, product, 'k', 'LineWidth', 1.5); hold on;
% 绘制积分区域(填充到当前x值)
fill([x(1:i), fliplr(x(1:i))], [product(1:i), zeros(1,i)], 'g',...
'FaceAlpha', 0.3, 'EdgeColor', 'none');
% 显示实时积分值
current_val = cumulative_integral(i);
text(pi/2, max(product)*0.8, sprintf('积分值: %.4f', current_val),...
'FontSize', 12, 'HorizontalAlignment', 'right');
title('乘积函数及积分过程');
xlim([-pi pi]); ylim([min(product)-0.2, max(product)+0.2]);
grid on; hold off;
% 捕获帧并写入GIF
frame = getframe(gcf);
im = frame2im(frame);
[imind, cm] = rgb2ind(im, 256);
if i == 1
imwrite(imind, cm, filename, 'gif', 'Loopcount', inf, 'DelayTime', 0.05);
else
imwrite(imind, cm, filename, 'gif', 'WriteMode', 'append', 'DelayTime', 0.05);
end
end
disp('动图生成完成!');
代码特点说明:
- 动态积分过程:通过绿色填充区域实时展示积分面积的累积过程
- 实时数值显示:在右下角动态更新当前积分值
- 三图联动显示:上方两个子图展示原始函数,下方子图展示乘积和积分过程
- 高效预计算:使用cumtrapz预先计算积分值提升性能
- 可调参数:通过修改step值可控制动画速度(step越小动画越慢)
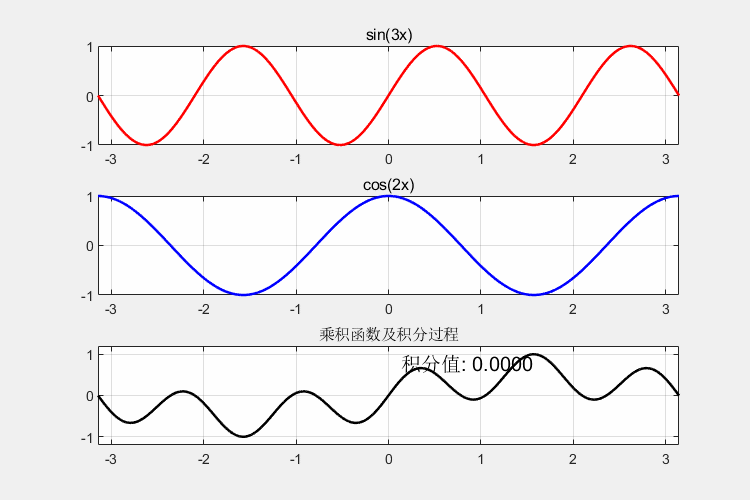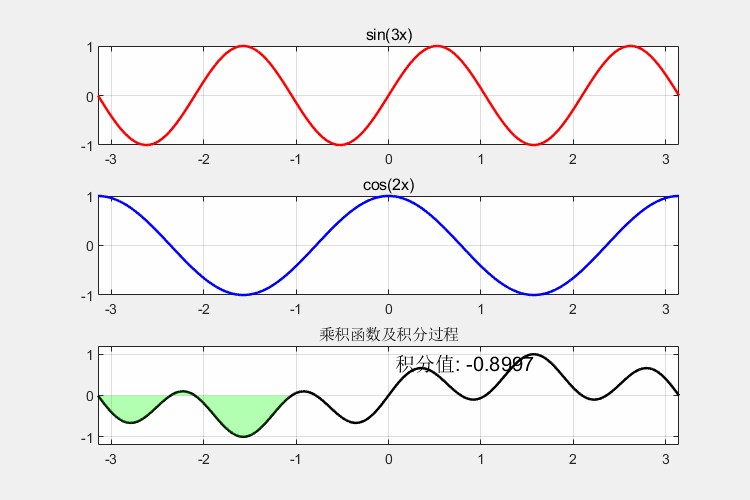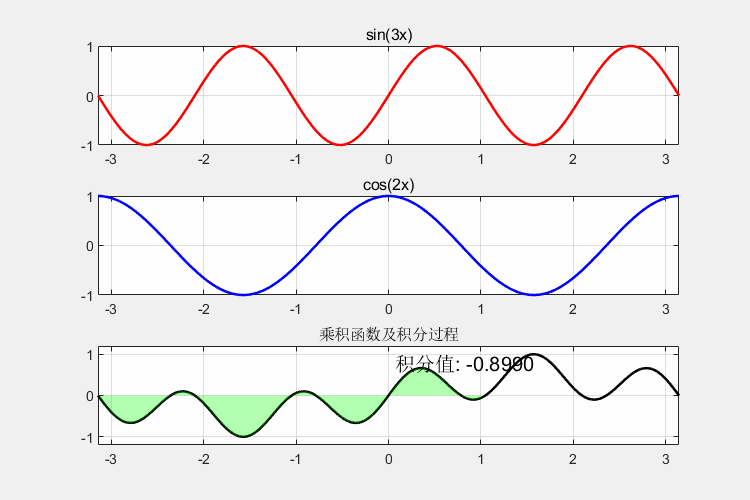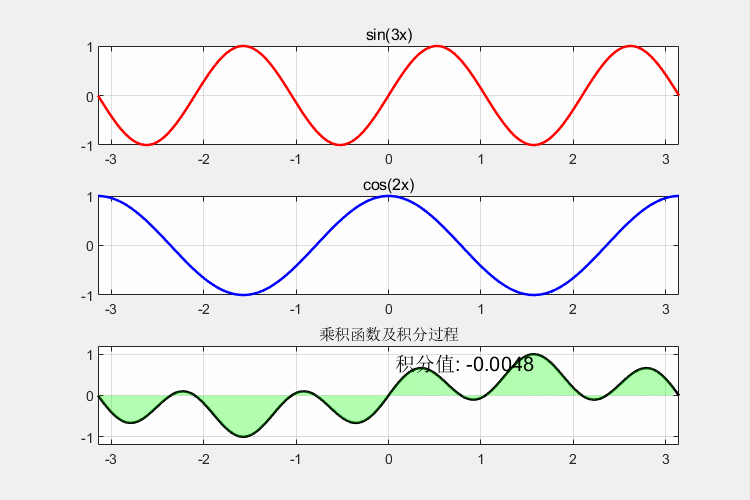
运行后生成的GIF将展示:
- 红色sin(3x)和蓝色cos(2x)的波形
- 黑色乘积曲线下方绿色填充区域的动态增长
- 积分值从0开始变化,最终趋近于0的正交性特征
注:最终积分值理论应为0,由于数值计算误差会显示接近0的小数值(如1e-16量级),这验证了三角函数系的正交性。
六、总结
三角函数正交性是数学分析中的重要性质,其推导基于三角函数的基本公式及其在周期内的积分特性。通过这一性质,我们能够进一步理解正交函数系在理论和应用中的广泛意义,为傅里叶分析和信号处理等领域奠定了基础。


























 1413
1413

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










