关于原神沙漠痕迹效果的完全解析

目录

前言

一、波形构造

1.1、高次幂函数尝试

1.2、导数连续的分段幂函数尝试

1.3、导数不连续的分段幂函数尝试

二、属性遮罩

2.1、归一化半径与时间

2.2、布尔高度混合

2.3、各shader之间的关联

三、法线计算

四、“故障”排查

4.1、自定义导数

4.2、模糊处理

4.3、胶囊形区域求最短距离

五、展望与资源链接

---

前言

——本文基于之前的痕迹效果分析文，针对轨迹的形状与淡化方式做进一步的探讨。(光是这个效果就又踩了半个月坑···）如果本文遇到些不太理解的操作，可以尝试先简单了解上一篇。

——其实倒也不至于说完全解析- -毕竟我目前并不会解包拆源代码这种操作-_-只是效果的大方向上，个人觉得做到了与游戏内基本一致。那么先上一波个人还原的效果。

一、波形构造

——为了实现上面的效果，相对于上次的“笔刷法线高度图”的绘制方式，本文在笔刷的实现上改为了定制化能力偏弱但可控性较强的程序纹理方式（不是我不想用旧方法- -···而是按旧方法走做不来原神里那种向中间聚拢的效果）。更具体的说，是利用函数曲线去构造轨迹的横截面波形。

——不论起伏多复杂的笔刷图，只要它是旋转对称的，那么其高度在数学上就总能表示为

z=f(r)r=x2+y2——的形式。所以我们一上来只需要关注二维情况下的高度函数f(r)的构造即可。而考虑到程序上的性能与便捷性，我们应当尽量用幂函数去构造f(r)。

——先来仔细看看原神里的轨迹横截面形状的变化。

1.1、高次幂函数尝试

——若是考虑衔接的顺滑（即导数连续），这个波形应当有坑底、波峰、外围边界这三个关键的控制点，并且这三个点导数为0。在幂函数的前提下，这至少是个4次函数。若是将坑底的深度、波峰的高度、外围的远近也公开为可独立调整的参数，幂函数的次数更是能达到5次。而求解这个5次函数的6个系数，考虑一般方法则需要一个6x6的系数矩阵求逆并做矩阵乘法。

——且不论矩阵乘法的计算量，单就形状的可控性而言，因为5次函数最多会有4个极值点，所以如上图所示，有一个游离的极值点可能会出现在给定的三个控制点中间，这是我们不希望看到的。

——所以这里我们退而求其次，考虑用分段函数的方法去构造波形。

1.2、导数连续的分段幂函数尝试

——在本人的初次尝试中，我将波形分成了如下三段。

——其中1是二次函数，2、3是三次函数，并且通过计算保证分段点的导数连续。

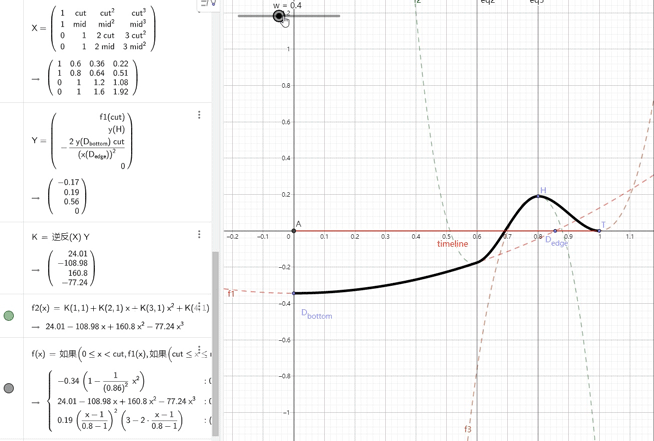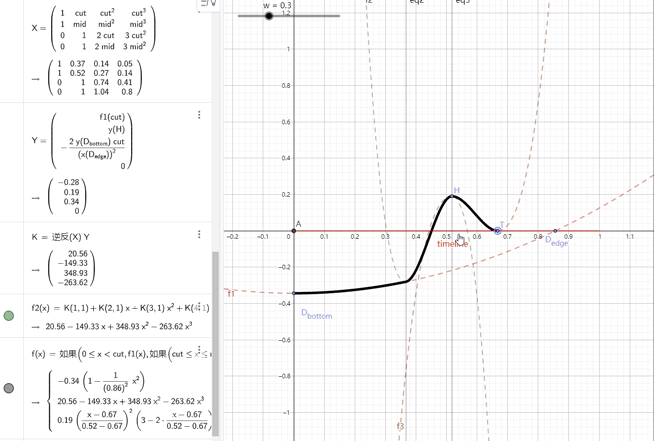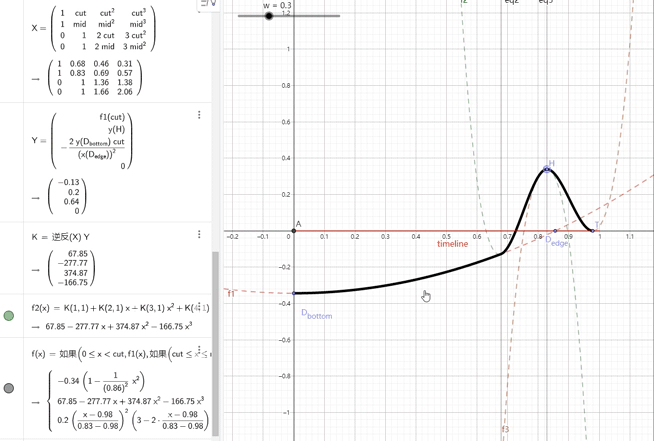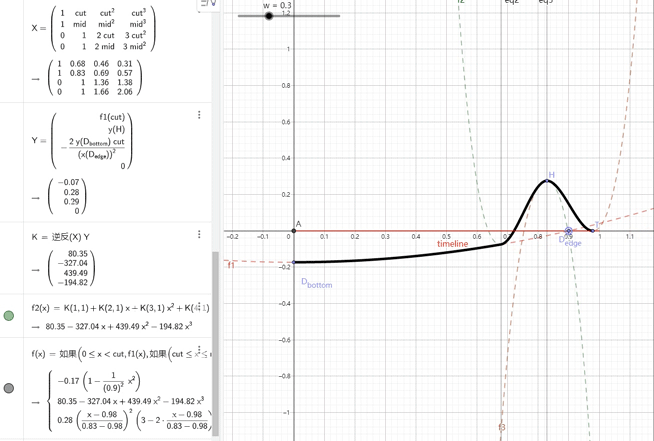
——虽然形状的控制上很像这么回事，但为了计算第二段的三次函数的系数，还是用到了一个4x4的矩阵。

——虽然在shader中算几个矩阵和行列式之类的也完全没问题（而不像我用来画函数的这个geogebra，开的久点函数多点就巨卡···），shader没有矩阵求逆也可以用克莱姆法则求5个行列式来解出4个系数（数学上是等价的），但经个人之前实际踩坑，其实分段点导数连续与否，对于模型的顶点密度来说，哪怕开了曲面细分也基本看不出来，是否连续的视觉感受主要还是靠后面的光照模型计算来体现（关于法线的计算后面会说，这里提前告知并不是用本节的高度函数直接求导算法线）。

——所以，既是为了数学模型尽可能简洁也是为了性能，这里我们再退一步- -不管分段点的导数连续了，直接躺平_(:з)∠)_

1.3、导数不连续的分段幂函数尝试

——最终，我直接用两个开口方向相反的二次函数来拼成我们需要的高度形状。