流形学习【Manifold Learning】

最新推荐文章于 2025-02-24 16:15:00 发布

薛定谔的猫ovo

最新推荐文章于 2025-02-24 16:15:00 发布

阅读量2.6k

点赞数 14

文章标签：流形学习降维

本文链接：https://blog.csdn.net/weixin_44162361/article/details/143844964

版权

1. 什么是流形(manifold)？

流形是局部具有欧几里得空间性质的拓扑空间。换句话说，流形是一个可以在局部范围内近似为欧几里得空间的空间。

欧几里得空间（Euclidean space） 是一类特殊的向量空间，它允许讨论长度、夹角等几何性质。
n维欧几里得空间表示为 $\mathbb{R}^n$ 是由所有n元有序实数元组构成的空间。
- 二维欧几里得空间 $\mathbb{R}^2$ ：由所有形如 $(x, y)$ 的有序对组成，可以表示平面上的所有点。
- 三维欧几里得空间 $\mathbb{R}^3$ ：由所有形如 $(x, y, z)$ 的有序三元组组成，用于描述物理世界中的空间位置。
性质
- 距离：欧几里得空间中两点的距离可以通过欧几里得距离公式计算 $d(\textbf{a},\textbf{b})=\sqrt{\sum_{i=1}^n(a_i-b_i)^2}$
- 角度：两个向量之间的角度可以通过它们之间的点积和模长来计算 $\text{cos}\ \theta = \frac{\textbf{a} \cdot \textbf{b}}{\|\textbf{a}\| \|\textbf{b}\|}$
- 内积空间：欧几里得空间是一个内积空间，其内积定义为两向量的点积

【e.g.】举例来说，地球表面就是一个二维流形的例子。尽管地球表面是一个三维空间的曲面，但是在局部范围内，地球表面看起来是平坦的（三维→二维）。意味着在小的区域内，我们可以使用二维坐标系（如纬度和经度）来描述地球表面上的点。

流形学习的观点：认为我们所能观察到的数据实际上是由一个低维流行映射到高维空间的。由于数据内部特征的限制，一些高维中的数据会产生维度上的冗余，实际上这些数据只要比较低的维度就能唯一的表示。

流形学习是一种机器学习和数据分析的方法，它专注于从高维数据中发现低维的非线性结构。
流形学习的基本假设是，尽管数据可能在高维空间中呈现，但是它们实际上分布在一个低维的流形上。
这个流形是数据的真实结构，它捕捉了数据中的内在关系和模式。

直观上来讲，一个流形就好比是一个d维的空间在一个m维(m>d)的空间中被扭曲之后的结果。【流形并不是一个形状，而是一个空间】

【e.g. 1】例如一个二维平面，将其扭到三维空间中，它就变成了一个流形，当然不扭的时候，它也是一个流形（欧式空间是流形的一种特殊情况）：

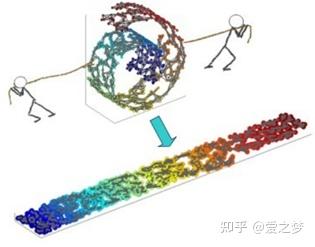
在这里插入图片描述

【e.g. 2】再比如对于球面上的一个点（三维空间中的点），可以用一个三元组来表示其坐标：在这里插入图片描述
但事实上，这个三维的坐标只由两个变量 $\theta$ 和 $\varphi$ 表示的，也可以说成它的自由度是2，正好对应了它是一个二维的流形。

流形学习的目标是从高维观测数据中恢复出对应的低维流形结构。

通常包含以下几个步骤：

数据预处理：包括归一化、去噪等，以确保数据的质量。
流形构造：通过各种算法（如Isomap、局部线性嵌入（LLE）、拉普拉斯特征映射（Laplacian Eigenmaps）等）来构造或近似表示数据的流形结构。
降维：将高维数据映射到低维流形上，以便于可视化、分析或进一步的机器学习任务。
分析与应用：在低维流形上进行数据分析，如聚类、分类、异常检测等。

流形学习在处理非线性数据结构时特别有效，它能够揭示数据背后的复杂关系，而不仅仅是通过线性变换来简化数据。

流形具有在局部与欧式空间同胚（homeomorphism，同胚是拓扑学概念，可以理解为同构，即两个空间存在同构映射关系）的空间，也就是它在局部具有欧式空间的性质，能用欧式距离来进行距离计算。

这就给降维带来了很大的启发，如果低维流形嵌入（embedding）到了高维空间，此时样本在高维空间的分布虽然复杂，但是在局部上仍具有欧式空间的性质，因此可以在局部建立映射关系，然后再设法将局部映射关系推广到全局。

当数据被降维到二维或三维时，就可以进行可视化，因此流形学习也可以被用于可视化。

流形学习方法是模式识别中的基本方法，分为线性流形学习算法和非线性流形学习算法。

非线性流形学习算法：等度量映射（lsomap），拉普拉斯特征映射（Laplacian eigenmaps，LE），局部线性嵌入（Locally-linear embedding，LLE）等
线性流形学习算法：对非线性方法的线性扩展，例如主成分分析（Principal component analysis， PCA），多维尺度变换（Multidimensional scaling， MDS）等

多维尺度分析（Multidimensional Scaling，简称MDS）核心思想：在低维空间中找到数据点的表示，使得这些点在低维空间中的距离尽可能地反映它们在原始高维空间中的相似性或距离。

【e.g.】一个可能的将点从三维空间映射到二维和一维空间的示例(未经优化的映射示例)。

在这里插入图片描述

MDS确保实际成对的距离与映射点的成对距离之间有最小的差异。

默认情况下，MDS中使用的距离度量是欧几里得距离。

在MDS中，存在两种主要的度量方式：

度量MDS：通过计算不同样本之间距离的度量值进行降维。
- 这种方法旨在保持原始数据中的点之间的欧几里德距离或其他度量距离在低维嵌入空间中的相对关系。
- 它试图在嵌入空间中尽可能准确地保持原始数据点之间的距离。
- 在优化过程中尝试最小化原始距离与嵌入距离之间的误差。
非度量MDS：仅考虑距离的排序信息。
- 在这种情况下，我们只知道原始数据点之间的相对排序关系，而不知道确切的距离或度量。
- 通过保持点的排序关系来在低维空间中嵌入数据。
- 它使用的度量是一种序关系度量，例如排名。

因此，在MDS中，“metric” 参数用于指定使用哪种类型的度量方式。如果设置为True，表示使用度量 MDS，而如果设置为False，表示使用非度量 MDS。度量方式的选择会影响嵌入结果和优化过程。