第一章 地下水数值模拟_数学模型

在不考虑水的密度变化的条件下，孔隙介质中地下水在三维空间的流动可以用下面的偏微分方程来表示：\frac{\partial }{\partial x}(Kxx \frac{\partial h}{\partial x})+\frac{\partial }{\partial y}(Kyy \frac{\partial h}{\partial y})+\frac{\partial }{\partial z}(Kzz \frac{\partial h}{\partial z})-W=Ss \frac{\partial h}{\partial t}

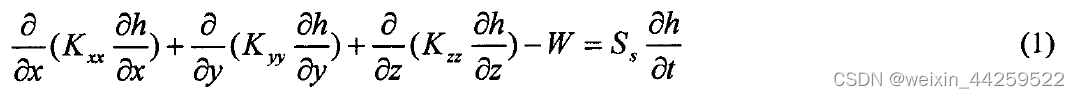其中:
Kxx，Kyy和Kzz为渗透系数在z、y和z方向上的分量。在这里，我们假定渗透系数的主轴方向与坐标轴的方向一致，量纲为(LT-1);
h：水头(L);
W︰单位体积流量(T-1)，用以代表流进汇或来自源的水量;

Ss︰孔隙介质的贮水率(L-1);
t︰时间（T)。

这个偏微分方程描述了地下水在孔隙介质中的三维流动，其中包含了渗透系数的各个方向分量 \( K_{xx} \)、\( K_{yy} \)、\( K_{zz} \)、水头 \( h \)、单位体积流量 \( W \)、孔隙介质的贮水率 \( Ss \) 和时间 \( t \)。

这个方程可以解释为以下几个方面的描述：

1. 扩散项：
   - 第一项表示 \( x \) 方向上的扩散，其流量受到 \( x \) 方向上渗透系数 \( K_{xx} \) 和水头 \( h \) 的影响。
   - 第二项表示 \( y \) 方向上的扩散，其流量受到 \( y \) 方向上渗透系数 \( K_{yy} \) 和水头 \( h \) 的影响。
   - 第三项表示 \( z \) 方向上的扩散，其流量受到 \( z \) 方向上渗透系数 \( K_{zz} \) 和水头 \( h \) 的影响。

2. 源项和汇项：
   - \( W \) 表示单位体积流量，可以代表水流进汇或来自源的水量，其影响被孔隙介质的贮水率 \( Ss \) 和时间 \( t \) 调节。

3. 时间变化项：
   - 最后一项表示水头 \( h \) 随时间 \( t \) 的变化率，描述了地下水位随时间的演变。

这个方程是一个三维空间中的偏微分方程，通过数值求解方法（如有限差分法、有限元法等），可以求解地下水位 \( h \) 在空间和时间上的分布情况，从而分析地下水在孔隙介质中的流动行为。

一般来说，Ss，Kxx，Kyy和Kzz都可能为空间的函数，而W可能不仅随空间变化，还可能随时间发生变化。公式(1)描述了在三维空间中，当渗透系数主轴和坐标系方向一致时，地下水在孔隙介质中的流动。有关这个公式的导出，读者可以在许多教科书中找到(如Rushton和Redshaw, 1979)。

公式(1)加上相应的初始条件和边界条件，便构成了一个描述地下水流动体系的数学模型。从解析解的角度上说，该数学模型的解就是一个描述水头值分布的代数表达式。在所定义的空间和时间范围内，所求得的水头h应满足边界条件和初始条件。但除了某些简单的情况，公式⑴的解析解一般很难求得。因此，各种各样的数值法被用来求得公式(1)的近似解。其中一种就是有限差分法。

是的，地下水流动的数学模型通常由偏微分方程（如公式（1）所示）以及相应的初始条件和边界条件组成。这个数学模型描述了地下水在空间和时间上的行为，通过求解这个模型，可以得到地下水位 \( h \) 在整个空间和时间范围内的分布情况。

通常情况下，这样的偏微分方程很难获得解析解，因此需要借助数值方法来求解。有限差分法是一种常用的数值方法之一，用于近似求解偏微分方程的解。它将求解区域离散化为网格，然后通过近似偏微分方程中的各个项，将偏微分方程转化为代数方程组，进而通过迭代求解这个方程组来得到近似解。

在应用有限差分法求解地下水流动问题时，通常需要考虑以下几个方面：

1. **网格划分：** 将求解区域划分为网格，确定网格的大小和形状。
2. **离散化方程：** 将偏微分方程中的各个项离散化，通常使用中心差分、向前差分或向后差分等方法。
3. **边界条件：** 确定边界条件，描述了地下水流动系统与外界的交互。边界条件可以是水头值、水流量或其他物理量。
4. **初始条件：** 确定初始时刻地下水位的分布情况。
5. **求解方程组：** 将离散化后的偏微分方程转化为代数方程组，然后通过迭代或直接求解方法求解这个方程组，得到地下水位的近似解。

通过这样的数值方法，可以得到地下水流动系统的近似解，进而进行地下水资源管理、地下水工程设计等工作。

在有限差分法求解过程中，连续的时间和空间被划分成为一系列离散的点。在这些点上，连续的偏导数也由水头差分公式来取代。将所求的未知点联合起来，这些有限差分式构成了一个线性方程组；然后对这个线性方程组进行联立求解。这样获得的解就是水头在各个离散点上的近似解。数值解虽然不能给出描述水头随时间和空间变化的代数表达式，但它可以用来解决大量的实际问题。

是的，有限差分法在求解地下水流动问题时将连续的时间和空间离散化为一系列离散的点，并使用水头差分公式来代替连续的偏导数。通过在离散点上构建有限差分方程，可以将偏微分方程转化为一个线性方程组。这个线性方程组可以用来描述地下水位在离散点上的近似解，然后通过联立求解的方法获得这些近似解。

在求解地下水流动问题时，通常需要执行以下步骤：

1. **网格划分：** 将求解区域划分为网格，确定网格的大小和形状，以及时间步长。
  
2. **离散化方程：** 在每个离散点上使用水头差分公式来代替偏导数，将偏微分方程离散化为一系列有限差分方程。

3. **建立线性方程组：** 将离散化的方程组合并成一个大的线性方程组，其中未知量是各个离散点上的水头。

4. **求解线性方程组：** 使用数值方法（如迭代法、直接法等）求解这个线性方程组，得到各个离散点上的水头近似解。

5. **后处理：** 对获得的近似解进行后处理，包括可视化、分析、验证等，以评估解的质量和适用性。

通过这样的数值方法，可以获得地下水在空间和时间上的近似解，用于解决地下水资源管理、地下水工程设计以及其他实际问题。虽然数值解无法给出水头随时间和空间变化的解析表达式，但它们可以为实际问题的求解提供有效的工具。

我们可以运用有限差分计算的方法对公式(⑴)以及相应的边界和初始条件求解。为了便于讨论，我们通过物理概念对有限差分法进行介绍。
 

离散化的概念
 

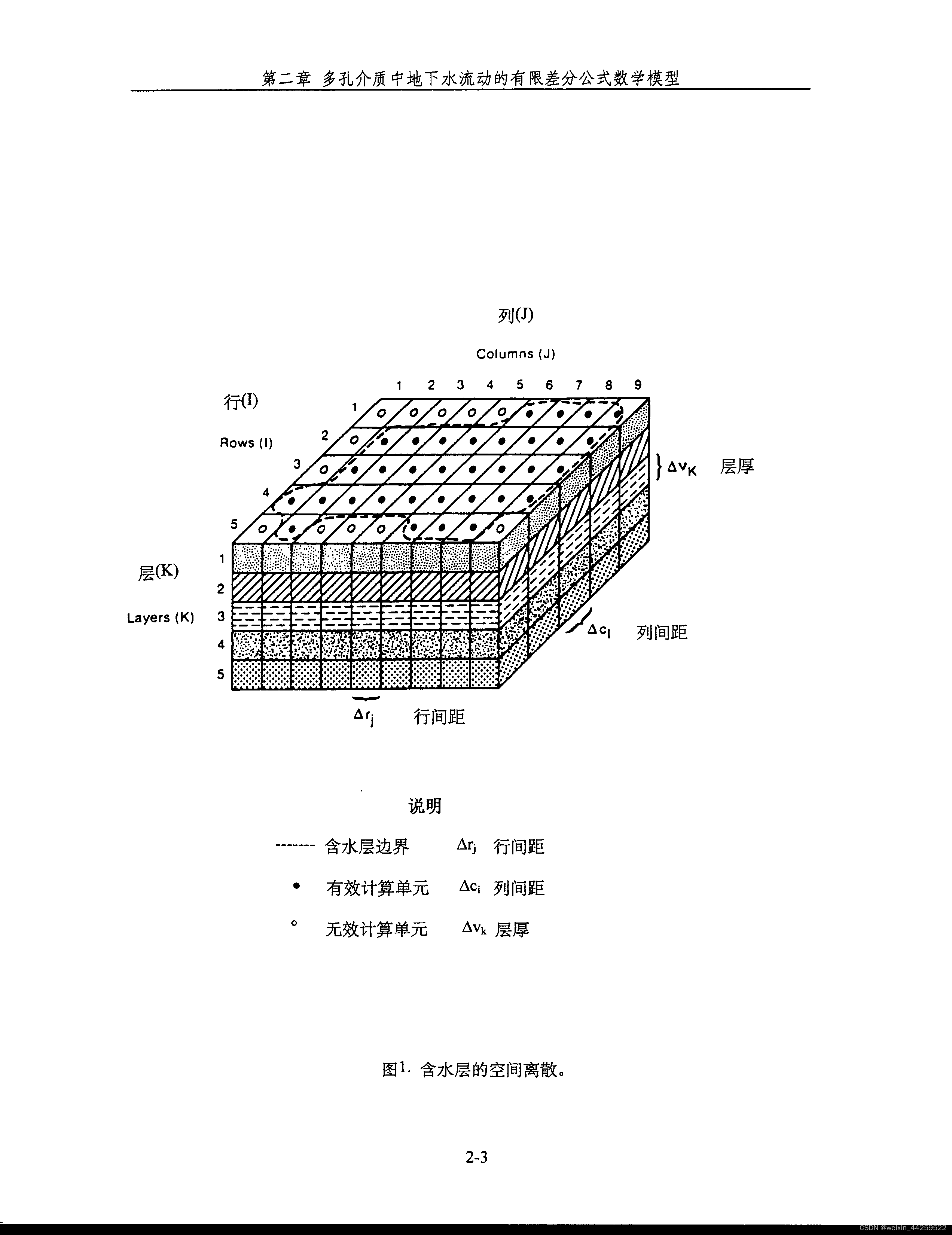
如图1所示，我们将一个三维含水层系统划分为一个三维的网格系统，整个含水层被剖分为若干层，每一层又剖分为若干行和若干列。这样，含水层就可以由许多剖分成的小长方体所表示。这些剖分出来的小长方体称为计算单元(Cell)。有时这些计算单元也称为元素或格点。[译注:在本书中，我们统一使用计算单元这个名称。]每个计算单元的位置可以用该计算单元所在的行号i)，列号j和层号(k)来表示。假定一个含水层可以剖分为“nlay”层，而每一层又剖分为“nrow”行和“ncol”列，则i称为行下标，j称为列下标,k称为层下标。显然，我们有

i- 1,2,..., nrow

j=1,2,..., ncol

k = 1,2,..., nlay

例如，在图1中所示的含水层系统被剖分为5层，5行和9列。在剖分过程中，我们一般尽量使模型的分层与实际含水层的水平分层一致。因此，在一个笛卡尔坐标系中，下标k通常沿竖直方向z而变化。在MODFLOW中，一个模型的第一层（即k=1）规定为最顶层，所以k的值随着高程降低而增加。MODFLOW还规定行的延伸方向与x轴平行，列的延伸方向与y轴平行。因此，下标（j）随x值的增加而增加，而行下标（i）随y值降低而增加。图1所示的标号就是依据这些规定所绘出的。值得注意的是，MODFLOW仅要求一个模型的行与列相互正交，而并不要求用户定义实际x-y-z坐标系。事实上，MODFLOW中所有计算并不需要知道计算单元（i，j，k）在空间坐标中的绝对坐标（x,y,z）。

按照图1所示的规定，某列j中的一个计算单元沿行方向上的宽度由Δrj所表示。某行i中的一个计算单元沿列方向上的宽度由Δci;所表示。层k中的计算单元的厚度则由Δvk所表示。在理论上，位于同一层中的所有计算单元应具有相同的厚度。但在实际工作中，同层计算单元的厚度也常常不样，以反映含水层厚度在空间中的变化。按上述定义，计算单元(4,8,3)的体积应为Δr8Δc4Δv3。

每个剖分出来的小长方体的中心位置称为节点。一个计算单元的水头实际上由水头在该节点的值所表示。正如图2所示，在一个二维平面上，有限差分法的计算可以分为两大类:单元中心法和结点中心法。不论采用哪种方法，整个含水层均由两组正交的平行线剖分为一系列单元。在单元中心法中，这些平行线构成了计算单元的边界。而在结点中心法中，结点位于这两组正交直线的交点上，计算单元的边界则位于两个相邻结点中线的位置上。无论采用哪种方法，在计算单元的划分过程中，应尽量保持每个计算单元中的水文地质参数为常数。
 

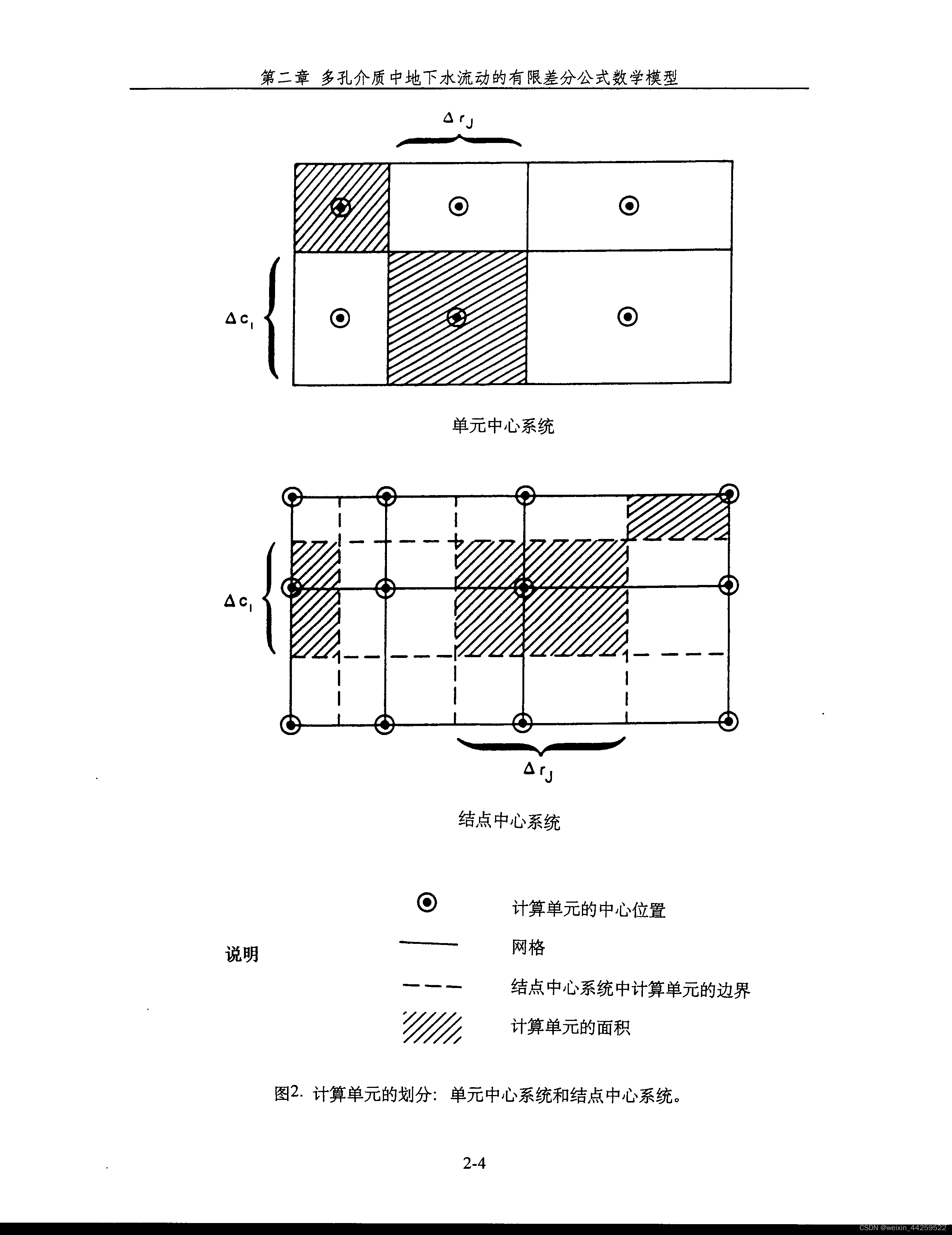
这两种剖分方法各有优缺点。二者之间的差别主要在于渗流边界的处理上。在单元中心法中，渗流边界总是位于计算单元的边线上。而在结点中心法中，渗流边界则与计算单元的中心位置相吻合。一般来说，在比较复杂的计算机程序中，由于对边界的数学处理比较容易，故多采用单元中心法。在MODFLOW中，也采用了单元中心法。然而，下面有关有限差分公式的推导，则适用于这两种方法。
由于所计算的水头值，既是空间的函数，也是时间的函数。因此，我们不仅得将含水层进行空间上的离散，同时也得对时间进行离散。
 

有限差分公式
 

地下水运动的有限差分公式实际上是根据地下水流动的连续性方程进行的。按照连续性方程，流入和流出某个计算单元的水流之差应等于该单元中贮水量的变化。当地下水的密度不变时，连续性方程可以简单地表示为:

公式(2)中的右侧项表示在单位时间内，当水头变化为Δh时含水层的贮水量变化。在这个公式中，仅表示了由于地下水的流人而引起的贮水量的增加。同理，如果流出的地下水量大于流入的地下水量，则含水层的贮水量应为减少。

迭代求解
 

差分方程的求解形式

计算单元的类型和边界条件的处理
 

有关垂向离散的讨论