第7章 有限差分法和有限元法的应用

7.1 解题过程
应用数值法解决实际问题,大致的工作步骤如下:
第一步 首先要明确模拟的目的,需要解决什么问题,以便确定模拟类型,选择适当
的模型(二维区域模型,二维剖面模型,准三维模型,三维模型)和相应的基本方程。
第二步 根据计算地区的地质、水文地质条件,计算问题的性质、要求、取水工程的类
型、布局等因素合理地确定所要计算渗流区的范围和边界性质,并圈定有越流区的范围
建立相应的概念模型和数学模型，
第三步 进行相应的网格设计和合理剖分。所谓合理剖分就是指剖分后形成的单元
应是正则单元,有限差分的网格最好用等距差分。有关正则单元的概念以后会专门谈。
第四步有限差分网格一般用(i,j,k)去标注格点/结点在行、列、层内的位置。有限
元法则要对每个结点、每个单元依次进行编号,还要任选一个直角坐标系,定出所有结点
的坐标值(x,y,z)和组成每个单元的所有结点的结点号(一般按逆时针方向顺序读数)
结点编号因为和最终形成的带宽有关,所以以后还要专门谈。单元编号除非程序中有特
殊要求，一般可以随意编。

对于非稳定流问题,两种数值方法都要确定时间步长和总的计算时段数。
第五步 确定参数值和有关资料(包括初值、边值、含水层厚度等),并转换到相应的
格点或结点、单元上。这些数据都要根据计算要求和源程序中输人这些数据的先后顺序
和格式要求-一整理好。
第六步 运行源程序,最终形成相应的差分方程组或线性代数方程组,解这些方程组
求出所有模拟时段各结点/格点的水头值或浓度(温度)值。
第七步
上述模拟结果与观测数据比较,误差是否足够小?如果是否定的,则要对参
数进行调整。重复第六、第七步,直至误差足够小,获得满意的结果为止。这样就完成了
模型的识别,从而初步确信模型能再现野外的水流/浓度状态。
第八步 运用经过识别的模型和参数原封不动地用来预报另一时间段的水流状态或
浓度(温度)分布状态,并与另一批野外观测资料对比,误差也要足够地小,从而完成模型
的检验;否则,需要重新进行模型的识别和检验。
第九步
考虑进行敏感度(灵敏度)分析。
第十步 根据模拟目的计算流量或其他需要计算的量、进行预报,输出模拟结果
第十一步 编写报告。
上述步骤中,第一、二、三、四、五步通常是人工完成的(如果条件允许采用规则网格
则四、五、六步有可能部分或全部由计算机自动完成),计算机及有关外部设施则可作为一种辅助工具。此因包括圈定计算区范围、确定边界性质等在内的建立概念模型,网格设计
等都必须根据具体条件作出某种正确的判断,所以尽管这些过程部分可以自动化,但目前
还不能完全靠计算机来实现。第六、七、八、九、十、十一步则通过适当的源程序连同第四、
五步整理的原始数据输入计算机后,由计算机分步完成。源程序可以自己编制,也可以选
择购买合适的现成商业软件,如MODFLOW、AQUIFEM-1等。如果从事某项专门目的
的研究因商业软件一般难以满足要求,必须自己编写源程序。

7.2 概念模型和网格设计
7.2.1
概念模型的建立
明确模拟目的后,首要任务就是建立概念模型。概念模型是地下水系统的一种近似
的形象化表示。其目的是为了简化野外实际问题,便于对该地下水系统进行分析,建立数
学模型,组织有关数据。虽然理论上,概念模型愈接近野外实际情况,数值模型就愈精确
可是一丝不差地再现野外地下水系统事实上是不可能的,简化是必要的。但它必须保持
原系统的基本特征,即所有主要的水文地质条件,以便能成为原系统的替代物,充分再现
原系统的特征。数值模拟的失败经常和概念模型有错或不能正确反映原系统的基本特征
有关,所以建立概念模型要非常小心。它常用立体图或剖面图来表示。建立与水流模型
有关的概念模型一般需要下列资料:
1)自然地理、地质资料。包括:①该地下水系统所在地区的地质图、剖面图、钻孔柱
状图和地形图:②)潜水含水层底板、承压含水层与相对隔水层(弱透水层)顶、底板等高线
图:③含水层厚度资料或等厚线图:④)岩溶(喀斯特)发育规律和不同水平的岩溶率;⑤显
示河流、湖泊沉积物范围、厚度的图件和资料。

2)水文地质资料。①所有含水层的等水位线图和等水压线图,显示各含水层间水力
联系,相对隔水层(弱透水层)缺失地段位置、范围的资料;②地下水水头、地表水水位和流
量的历时观测资料和观测孔、水文站的位置;③显示含水层、弱透水层渗透系数或导水系
数以及贮水系数(或贮水率)分布的平面图、剖面图;④河流、湖泊沉积物的分布及其渗透
系数的资料;⑤蒸发-蒸腾速率、地下水补给速率(或降水量、入渗补给系数)和地面水-地
下水交换速率的时(间)空(间)分布资料,抽(注)水井、矿井位置及其抽水流量的时空分布
资料,地下水天然排泄流量时空分布资料;⑥取水工程、疏于工程的设计布局、设计流量
或允许降深、疏干问题中需要疏千的范围、要求降深、疏干时间等。
对于地下水污染等水质问题则还需要地下水、河/湖水和降水中溶质浓度的历时观测
资料、弥散度、污染源等的资料。
建立概念模型的第一步就是识别模型边界、圈定计算区。这一步很重要,因为它不仅
影响计算工作量,更重要的还在于它影响数学模型建立得正确与否。计算区应尽可能是
-个比较完整的水文地质单元,以便在计算中能正确地反映该地区的水文地质特征。所
以应尽可能把地下水系统的天然水文地质边界作为模型边界。有时由于种种原因难以做
到这点,只能根据计算区的地质、水文地质条件,计算问题的性质、要求,取水工程的类型、布局等因素合理地选取比天然边界所圈定的区域要小的范围作为计算区。不论何种情
况,在构建概念模型时都要对地下水系统的真实水文地质边界进行识别。建立概念模型
需要做的工作主要有下列三步:①确立含水岩组;②进行均衡估算;③确立含水系统。

确定含水岩组是建立概念模型的重要
步。含水岩组由水文地质性质相似的若干地
质单元组成。地质上的几个岩层可以组成一
个含水岩组,地质上的一个岩层也可以分为
几个含水层和相对隔水层。华北石炭系太原
组由石英砂岩、页岩夹多层灰岩和煤层组成，
厚60~150m。显然，一般不能把太原组作为
一个计算单位。要把几层灰岩分出来作为几
个含水层,其余则作为若干个相对隔水层来
处理。例如焦作煤田部分矿区,中奥陶统灰
岩中的地下水通过断裂补给太原组第八、第
二(L、L2)灰岩中的地下水,成为矿井突水水
源,所以L、L灰岩单独作为模拟目的层对
评价某些矿区的涌水量问题来说是非常必要
的(图7.1)。反过来。在一些小比例尺的大
区域模拟中,往往把华北的整个寒武一奥陶
系当成一个含水岩组,加以模拟。所以需要
因地因情况而异来确定含水岩组。地质资料
不足,会给划分含水岩组带来困难,这时沉积
相的知识可以帮助我们了解沉积环境,如古
河道在哪儿?以恢复沉积历史，正确划分含
水岩组。

为了正确划分含水岩组有时需要其他方
面的一些资料,如巨厚砂岩如果仅仅根据地
层界限来划分模拟目的层有时会得出不恰当
的结果。此时电测井的资料有助于划分含水岩组,如图7.2直接根据电测井曲线划分含水岩组,而没有考虑地层界限。有时区域水位
资料也可以帮助我们在厚的砂、黏土互层序列中识别具有相同水文地质性质的层位,划分
模拟目的层(图7.3)。当钻孔穿过1800~2600ftФ的厚层砂层时,出水了。水位埋深较
上、下层的水位埋深大,反映出这儿有一个渗透性大的带,其上下都是渗透性较差的介质
所以在概念模型中有必要专门设一层来代表这个带。从而根据4组不同的水位资料确定
了4个层。
确定含水岩组时还要考虑研究区范围的大小,图件比例尺。如果范围大、比例尺小，就要把水文地质性质相近的相邻地层单位合并为一个含水岩组。如整个柳林泉域面积超
过 7000km,仅仅泉域内含水层的分布面积也有2700km左右,作为研究柳林泉域的区
域水流模型,在这种情况下已没有必要来区分奥陶系、寒武系中的各个层组,如前述合并
为一个寒武-奥陶系裂隙-岩溶含水岩组是恰当的。显然在这种情况下,需要详尽掌握当
地的地层、岩性及其渗透性的资料。

 

含水岩组组成了概念模型的骨架,但仅有含水岩组还是不够的,还必须根据水文地质
资料来分析该地下水系统的补给、径流、排泄条件,地下水流向、补给区、排泄区的位置以
及含水层和地表水间的关系,掌握地下水的来龙去脉,以便形成清晰的地下水流动系统。
在这项分析中,除了应用传统的水文地质方法外,灵活应用有关知识也非常重要。分析水
流系统时,需要综合分析所掌握的有关降水、蒸发、地表径流以及地下水水头、水化学资
料。地下水水位(头)资料可以帮助我们确定地下水流向、补给区和排泄区的位置以及地
下水和地表水之间的关系、各个含水层地下水之间的关系。有时正确应用水化学资料有
助于推断水流方向、判断水的来源和补给量,甚至有助于区分局部的、中间的和区域的地
下水流动系统。

7.2.2 模型类型选择
常用的模型有:二维区域模型、准三维模型、剖面模型和三维模型。
二维区域模型适用于研究承压含水层、越流含水层、潜水含水层和承压-无压含水层
用于承压含水层时,需要给出每个单元或结点/格点上的导水系数和贮水系数值。如果是
各向异性含水层则z方向和y方向的导水系数(T=K_M和T„=KM)是不同的
用于越流系统时,模型并不特别表示出弱透水层(相对隔水层)和供给越流水源的含水层
而是用在主含水层的方程中加一项越流项

来表示,式中:K,和m'分别为弱透水层的垂向渗透系数和厚度;H为主含水层的水头;
H,为供水源含水层(或河流)的水头。越流系统的供水源可以是另-个承压含水层或潜
水含水层或地表水体。模拟时通常假设这个水头H,是不变的,如果发生变化,那就不能
采用这类模型了,必须单独给作为供给水源的含水层建立方程。这类模型的另一个假设
就是没有水从弱透水层的贮存中释放出来。Trescott等(1976)认为弱透水层内水的短暂
释放仅仅出现在时间t,=S'm'/2K.内(式中,S'为弱透水层的贮水系数)。显然忽略了这
种释放会给解带来误差,为此Trescott等给越流项加了一个修正项。显然,三维模型可
以更好地模拟这种影响。
二维区域模型用于潜水含水层时,要应用Dupuit 假设,假设在z方向水头没有变化
需要的数据有:渗透系数、给水度、厚度和含水层底板标高。如果不用Dupuit 假设,则要
用剖面模型或三维模型。用于天然条件下可能出现、或在承压含水层中过量抽水后可能
形成的承压-无压含水层时，上述各类数据就都需要了。
准三维模型可以用来模拟由多个含水层和弱透水层组成的含水系统。在这里和在
维区域模型一样,弱透水层的作用并不明显地表示出来,即不考虑弱透水层本身的弹性释
水,只考虑弱透水层内的垂向流动,即上下含水层间由于存在水头差通过弱透水层发生的
垂向水量交换。此时弱透水层的作用仅用代表两含水层间垂向水流运动的越流项来
拟。为此要求含水层和弱透水层的渗透系数差两个数量级或两个数量级以上,此时忽略
弱透水层内水平运动给模拟目的层内水头造成的误差小于5%(Neuman&Witherspoon，1969)。如果两者渗透系数的差小于两个数量级,就不宜采用这类模型,应改用三
维模型。准三维模型需要准备各结点/格点或单元的下列数据:上部潜水含水层的渗透系
数、给水度和底板标高,下部各含水层的导水系数(T_和T)、贮水系数,弱透水层的垂
向渗透系数和厚度。
三维模型能很好地刻画地下水的实际流动情况。
二维剖面模型能反映垂向水流的运
动情况,但应注意二维剖面模型无法刻画井的流量,因而无法在有井的情况下的使用这种
模型,从而大大限制了它的应用范围。当垂向水头梯度的变化重要时,潜水含水层要用剖
面二维模型或三维模型来模拟,在这种情况下,潜水面和渗出面(如果存在的话)要作为边
界的一部分。无论有限差分法还是有限元法都能模拟剖面上的含水层,但处理潜水面和
渗出面的移动,有限元法要比有限差分法容易得多。需要考虑弱透水层释水时,则要用三
维模型。三维模型需要的数据除了必须给出每层的参数外,基本上和二维区域模型相似
即各层的顶、底板高程、渗透系数、贮水率。但要注意一些数据如水头应该是三维的,即需
要有同一地点不同深度的水头观测资料。剖面模型需要的数据和三维模型类似。
具体选用哪种模型要综合考虑所研究问题的性质、具体模拟要求,当地地质、水文地
质条件,所掌握的数据资料,特别是长期观测资料以及模拟经费和时间。能用二维区域模
型解决、满足模拟要求的问题千万不要贸然采用三维模型,因为后者不仅需要大量三维观
测数据(水头、浓度等)和资料,一般难以满足,而且工作量大,耗费的机时和经费多,如果
没有足够的资料,模拟结果很可能不一定理想。至于一般的地下水资源评价问题用二维
区域模型或准三维模型就足够了。

7.2.3 网格设计与剖分
数值模拟中,连续的研究区将为由结点和有关的有限差分网格或有限个单元组成的
离散域所代替。选择什么样的模型将决定网格的维数,选择何种数值方法(有限差分法或
有限元法等)将决定网格的结构。
1.网格类型
如前述,有限差分法有两种网格:结点法和格点法。两者差别只在对第二类边界条件
的处理上。网格布置时,由于边界形状不规则会使一部分结点位于边界以外,成为界外结
点。这些界外结点也要占用内存,所以应使这类结点尽可能地少。采用结点法时,应小心
地使结点直接落在边界上。采用格点法则应使第二类边界位于网格边上,第一类边界位
于格点上。国外许多软件如MODFLOW用的就是格点法,PLASM虽然用了格点法,但
它可视用户需要转换为结点法。有限元法在网格设计上允许有更大的灵活性。所用基函
数的性质决定了单元是线性的,或二次的、三次的。通常采用线性单元。AQUIFEM-1软
件用的就是线性三角形单元。有些软件可以混合采用三角形和四边形单元。
2.模拟目的层
概念模型可以帮助我们确定模拟的目的层是一个,还是几个。显然,一个含水岩组的情况只要一个目的层。在有多个含水岩组的情况下,模拟目的层的选定就和模拟的目的、
要求、地质、水文地质条件有关了。模拟目的层确定以后,模型的类型也就选定了。
需要注意,准三维模型假设含水层是水平的,因此倾斜地层只有当地层倾角很小时
才能用水平模拟目的层来代表这些倾斜地层,否则还是用三维模型为好。为了让读者了
解国外准三维模型的应用,有必要介绍一下Phillips用准三维模型模拟Delaware 州倾角
不大的倾斜含水岩组的情形(图7.4)。地下水从潜水含水层1向下补给三个含水层。潜
水含水层对含水层2的补给由含水层1的给定水头的结点和含水层1和2之间的越流系
数值来计算。潜水含水层与其他二个含水层3和4的关系则用和含水层2、3左侧二个矩
形阴影区的与含水层1中水头相当的给定水头及越流性质来模拟。这些阴影区的三个边
为零流量边界,第四条边界则通过越流项和含水层3和4联系起来。在准三维模型中如何处理含水层或弱透水层(隔水层)的尖灭,可以考虑采用图7.5介绍的方法。

3.网格定向
模拟各向异性介质时,在平面上应使x,y轴和渗透系数的主方向平行，即与K，
K平行。当模型有z轴时还要和K_平行。但实际上有时做不到,如图7.6所示,垂向
坐标轴和地层层面并不垂直。此时通常用的一种方法是假设地层倾角小到足以假设
主方向近似地与纵轴平行。如果不可能做到这一点,且各向异性的影响又很重要,那解决
办法只有在控制方程中写出渗透系数的各个对角线分量了。有限元法要做到这一点比较
容易。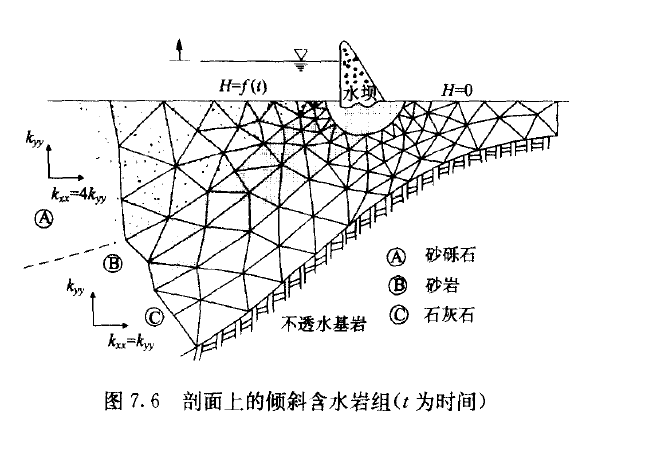

有限元法能尽可能较精确地反映边界的形状。有限差分法经过特殊处理后虽然也能
模拟复杂的不规则边界,但要注意一般商用软件中并不包含这些方法。因此在这种情况
下,宁可采用有限元法了,因为它比修改一个有限差分法软件要方便得多。
最后应指出,选取边界时应使它远离影响区、特别是抽水中心,以便抽水的影响达不
到所选定的边界。如不注意这点必然会给模拟结果带来很大的误差,很多模拟预测与后
来的实际结果相差很大,主要原因就在这里。如果能做到这点,那网格对边界形状的精确
拟合对模拟结果来说就不是决定性的了(Anderson&Woessner,1992)。