关于ACF以及PACF在时间序列分析中的应用---ARIMA滞后项阶数确定(附代码）

原理背景

在时间序列建模中，我们常用到的一个模型就是ARIMA，但是在使用该模型时，一个问题就是如何确定AR,MA中的p和q,即滞后项的级数。这时，一般我们会采用ACF(auto-correlation function) 以及PACF(partial auto-correlation function)来确定。

关于ACF以及PACF的理解，这里推荐一篇非常棒的英文博客:
Significance of ACF and PACF Plots In Time Series Analysis

然后这里我就文章的内容做一些说明。

0.假设我们已经通过差分(difference)得到了一个平稳(stationary)时间序列。

1.首先，我们先来看一下AR(auto regressive process)部分级数p的确定。我们会使用PACF,为什么不使用ACF来确定呢？原因就是在ACF中即使是非常滞后的项也可能显示很高的相关性，因为该滞后项可以通过影响靠前的滞后项间接影响当前时间节点的数值。为了排除这种影响，我们引入PACF，对于滞后项xt-m,其与xt的PACF相关系数为剔除前面所有滞后项xt-1,xt-2,xt-3,…xt-(m-1)之后的值。也就是说，该值能更加精准的反映出该滞后项自身对当前时间节点的影响，因此用PACF来确定AR滞后项级数会比ACF更有说服力。

2.然后我们来考虑MA(moving average process)。也就是说我们假定我们的目标序列是一个由随机扰动滞后项形成的序列。

这时，我们不应该选择使用PACF来确定滞后项的级数。为什么呢？因为对于这样的序列，不存在说某个单独的滞后项(随机扰动)会直接影响当前时间节点的值，而这恰恰是PACF能得到的，因此在这里PACF就失去了它的价值。因此在这里我们会选择使用ACF作为级数的确定标准。

实例

下面是一个基于R语言的应用实例。

library(forecast)
year=trunc(time(AirPassengers))
month=cycle(AirPassengers)
dataset=cbind(year, month, AirPassengers)
data=data.frame(dataset)

Tseries=ts(data$AirPassengers,frequency=12,start=c(1949,1))

#train/test sets
train=window(Tseries,start=c(1949,1),end=c(1959,12))
test=window(Tseries,start=c(1960,1),end=c(1960,12))

#acf to original time series
Acf(train,lag.max=36)
#pacf to original time series
Pacf(train,lag.max=36)

#从acf的拖尾结果可以看出，该时间序列非平稳，因此我们需要对其差分处理
#这里同时考虑差分以及季节差分（消除季节的周期性）

#我们需要先确定差分次数
N_DIFF=ndiffs(train)
N_SEAS_DIFF=nsdiffs(train)
DIFFS=data.frame(N_DIFF,N_SEAS_DIFF)

#差分后序列的Acf&Pacf
#根据前面的最佳差分次数的结果,普通差分（外层,lag=1）与季节差分（内层，lag=12）各进行一次
#这里对train做log的意义在于将Multiplicative model 转化为 addative model,方便差分
Acf(diff(diff(log(train),12),1),lag.max=36)
Pacf(diff(diff(log(train), 12),1), lag.max=36)


#接下来,尝试不同的模型
air_arima_1=Arima(train, lambda=0, order=c(0,1,0), seasonal=c(0,1,0))
air_arima_2=Arima(train, lambda=0, order=c(1,1,0), seasonal=c(0,1,0))
air_arima_3=Arima(train, lambda=0, order=c(0,1,0), seasonal=c(1,1,0))
air_arima_4=Arima(train, lambda=0, order=c(0,1,1), seasonal=c(0,1,0))
air_arima_5=Arima(train, lambda=0, order=c(0,1,0), seasonal=c(0,1,1))
air_arima_6=Arima(train, lambda=0, order=c(0,1,1), seasonal=c(0,1,1))
air_arima_7=Arima(train, lambda=0, order=c(1,1,1), seasonal=c(0,1,1))
air_arima_8=Arima(train, lambda=0, order=c(0,1,1), seasonal=c(1,1,1))
air_arima_9=Arima(train, lambda=0, order=c(1,1,1), seasonal=c(1,1,1))
air_arima_auto=auto.arima(train, lambda=-0)

#aic
aic_corr=rbind(air_arima_1$aicc , air_arima_2$aicc , air_arima_3$aicc , air_arima_4$aicc , air_arima_5$aicc , air_arima_6$aicc, air_arima_7$aicc, air_arima_8$aicc, air_arima_9$aicc, air_arima_auto$aicc )
rownames(aic_corr)=list("arima_1", "arima_2", "arima_3", "arima_4", "arima_5", "arima_6",  "arima_7", "arima_8", "arima_9", "arima_auto")


#order info
arima_orders=rbind(air_arima_1$arma , air_arima_2$arma , air_arima_3$arma , air_arima_4$arma , air_arima_5$arma , air_arima_6$arma, air_arima_7$arma, air_arima_8$arma, air_arima_9$arma, air_arima_auto$arma)
arima_orders=arima_orders[,c(1,6,2,3,7,4,5)]

results=data.frame(aic_corr,arima_orders)
results

#forecast
air_arima_1_fc=forecast(air_arima_1, h=12)
air_arima_2_fc=forecast(air_arima_2, h=12)
air_arima_3_fc=forecast(air_arima_3, h=12)
air_arima_4_fc=forecast(air_arima_4, h=12)
air_arima_5_fc=forecast(air_arima_5, h=12)
air_arima_6_fc=forecast(air_arima_6, h=12)
air_arima_7_fc=forecast(air_arima_7, h=12)
air_arima_8_fc=forecast(air_arima_8, h=12)
air_arima_9_fc=forecast(air_arima_9, h=12)
air_arima_auto_fc=forecast(air_arima_auto, h=12)

#compute accuracy
acc_arima_1=accuracy(air_arima_1_fc ,test)
acc_arima_2=accuracy(air_arima_2_fc ,test)
acc_arima_3=accuracy(air_arima_3_fc ,test)
acc_arima_4=accuracy(air_arima_4_fc ,test)
acc_arima_5=accuracy(air_arima_5_fc ,test)
acc_arima_6=accuracy(air_arima_6_fc ,test)
acc_arima_7=accuracy(air_arima_4_fc ,test)
acc_arima_8=accuracy(air_arima_5_fc ,test)
acc_arima_9=accuracy(air_arima_6_fc ,test)
acc_arima_auto=accuracy(air_arima_auto_fc ,test)
performance=rbind(acc_arima_1 , acc_arima_2 , acc_arima_3 , acc_arima_4 , acc_arima_5 , acc_arima_6, acc_arima_7 , acc_arima_8 , acc_arima_9, acc_arima_auto )

rownames(performance)=list("Arima_1 Train","Arima_1 Test", "Arima_2 Train","Arima_2 Test", "Arima_3 Train","Arima_3 Test", "Arima_4 Train","Arima_4 Test", "Arima_5 Train", "Arima_5 Test", "Arima_6 Train", "Arima_6 Test",
                              "Arima_7 Train","Arima_7 Test", "Arima_8 Train", "Arima_8 Test", "Arima_9 Train", "Arima_9 Test","Arima Auto Train", "Arima Auto Test")

performance=performance[,1:6]

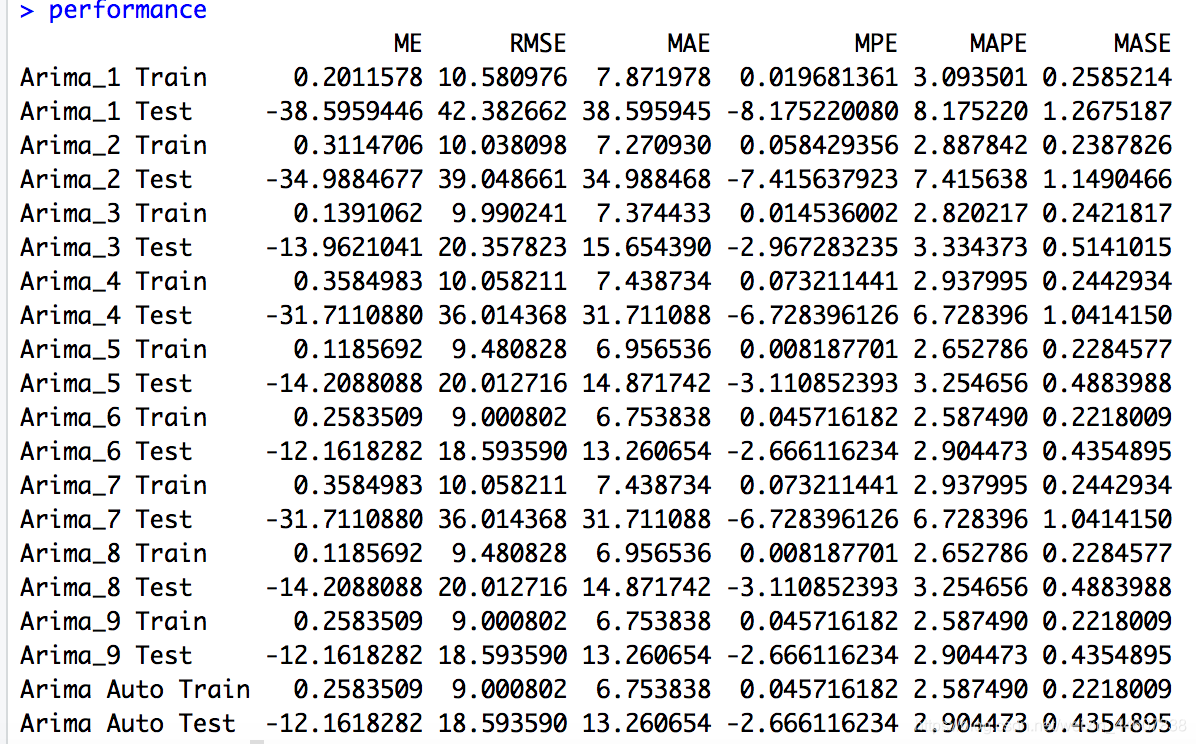
下面是不同order次数下的模型在训练集以及测试集上的表现。