FITS: MODELING TIME SERIES WITH 10k PARAME- TERS

系列文章目录

---

---

ABSTRACT

在本文中，我们介绍了 FITS，一种轻量级但功能强大的时间序列分析模型。 与直接处理原始时域数据的现有模型不同，FITS 的运行原理是可以通过复杂频域中的插值来操纵时间序列，从而实现与时间序列预测和异常检测任务的最先进模型相当的性能。 值得注意的是，FITS 通过大约 10k 参数的精简配置来实现这一目标，使其非常适合边缘设备，并为广泛的应用铺平了道路。 代码可用：https://github.com/VEWOXIC/FITS。

---

一、引言

时间序列分析在从医疗保健设备到智能工厂的众多领域中发挥着关键作用。 在这些领域中，通常依赖智能传感器等边缘设备，这些设备由计算和内存资源有限的 MCU 驱动。 时间序列数据以其固有的复杂性和动态性为标志，通常呈现时域内稀疏且分散的信息。 为了有效利用这些数据，最近的研究提出了复杂的模型和方法（Zhou et al., 2021；Liu et al., 2022a；Zeng et al., 2023；Nie et al., 2023；Zhang et al., 2022）。 然而，这些模型的计算和内存成本使得它们不适合资源受限的边缘设备。

另一方面，时间序列数据的频域表示可以更紧凑、更有效地描述固有模式。 虽然现有研究确实已经利用频域进行时间序列分析——FEDformer（Zhou et al., 2022a）使用频谱数据丰富其特征，而 TimesNet（Wu et al., 2023）利用高振幅频率通过以下方式进行特征提取： CNN——频域紧凑性的综合利用在很大程度上仍未被探索。 具体来说，没有利用频域使用复数来捕获幅度和相位信息的能力，导致持续依赖计算密集型模型来提取时间特征。

在本研究中，我们将时间序列分析任务（例如预测和重建）重新解释为复杂频域内的插值练习。 本质上，我们通过对所提供的片段的频率表示进行插值来生成扩展的时间序列片段。 具体来说，对于预测，我们可以通过简单地通过频率插值扩展给定的回顾窗口来获得预测结果； 为了重建，我们通过内插其下采样对应部分的频率表示来恢复原始片段。 基于这一见解，我们引入了 FITS（频率插值时间序列分析基线）。 FITS 的核心是复值线性层，经过精心设计，用于学习幅度缩放和相移，从而促进复频域内的插值。

值得注意的是，虽然 FITS 在频域中进行插值，但它基本上仍然是时域模型，集成了 rFFT（Brigham & Morrow，1967）操作。 也就是说，我们使用 rFFT 将输入段变换到复频域进行频率插值。 然后，该内插频率数据被映射回时域，从而形成一个可供监控的细长段。 这种创新设计使 FITS 具有高度适应性，可以无缝地融入大量下游时域任务，例如预测和异常检测。

除了其流线型线性架构外，FITS 还包含一个低通滤波器。 这确保了紧凑的表示，同时保留了基本信息。 尽管很简单，FITS 始终实现最先进的 (SOTA) 性能。 值得注意的是，在大多数情况下，FITS 用少于 10k 的参数实现了这一壮举。 这使得它比轻量级时间线性模型 DLinear（Zeng 等人，2023）紧凑 50 倍，比其他主流模型小约 10,000 倍。 鉴于其内存和计算效率，FITS 成为部署的理想选择，甚至可以直接在边缘设备上进行训练，无论是用于预测还是异常检测。

总之，我们的贡献可以概括如下：

• 我们推出了 FITS，一种用于时间序列分析的超轻量级模型，拥有 5k∼10k 范围内的适度参数数量。
• FITS 通过采用复值神经网络提供了一种开创性的时间序列分析方法。 这可以同时捕获幅度和相位信息，为更全面、更有效地表示时间序列数据铺平道路。
• 尽管比大多数主流模型小几个数量级，FITS 在一系列时间序列分析任务中始终如一地提供顶级性能。

2 RELATED WORK AND MOTIVATION

2.1 FREQUENCY-AWARE TIME SERIES ANALYSIS MODELS

时间序列分析的最新进展见证了频域信息的利用来捕获和解释潜在的模式。 FNet（Lee-Thorp 等人，2022）利用纯粹的基于注意力的架构来有效地捕获仅在频域中的时间依赖性和模式，从而消除了对卷积层或循环层的需要。 另一方面，FEDFormer (Zhou et al., 2022a) 和 FiLM (Zhou et al., 2022b) 将频率信息作为补充特征，以增强模型捕获长期周期性模式的能力并加快计算速度。

另一条工作旨在捕获数据固有的周期性。 例如，DLinear（Zeng et al., 2023）采用单个线性层从时域中提取主要周期性，并超越了一系列基于深度特征提取的方法。 最近，TimesNet（Wu et al., 2023）通过识别多个主导频率而不是依赖单个主导周期性，取得了最先进的结果。 具体来说，他们使用快速傅里叶变换（FFT）来找到能量最大的频率，并根据其周期将原始的一维时间序列重塑为二维图像。

然而，这些方法仍然依赖于特征工程来识别主导周期集。 基于能量选择该组可能仅考虑主导周期及其谐波，从而限制了捕获的信息。 此外，这些方法仍然被认为效率低下并且容易过度拟合。

2.2 DIVIDE AND CONQUER THE FREQUENCY COMPONENTS频率分量的划分

将时间序列视为信号使我们能够将其分解为正弦分量的线性组合，而不会丢失任何信息。 每个分量都具有独特的频率、初始相位和幅度。 直接对原始时间序列进行预测可能具有挑战性，但预测每个频率分量相对简单，因为我们只需要根据时移对正弦波应用相位偏差。 随后，我们将这些移位的正弦波线性组合以获得预测结果。

这种方法有效地保留了给定回溯窗口的频率特征，同时保持回溯窗口和预测范围之间的语义一致性。 具体来说，得到的预测值以合理的时间偏移保持原始时间序列的频率特征，确保保持语义一致性。

然而，在时域中预测每个正弦分量可能很麻烦，因为正弦分量被视为一系列数据点。 为了解决这个问题，我们建议在复频域中进行这种操作，这提供了更紧凑和信息丰富的表示，如下所述。

3 METHOD

3.1 PRELIMINARY: FFT AND COMPLEX FREQUENCY DOMAIN

快速傅里叶变换（FFT，（Brigham & Morrow，1967））可有效计算复数序列的离散傅里叶变换 (DFT)。 DFT 将离散时间信号从时域变换到复频域。 在时间序列分析中，当处理真实输入信号时，通常会使用真实 FFT (rFFT)。 它将 N 个实数的输入压缩为 N/2+1 个复数序列，表示复频域中的信号。

Complex Frequency Domain

在傅里叶分析中，复频域是信号的表示，其中每个频率分量都用复数来表征。 这个复数捕获了分量的幅度和相位，提供了全面的描述。 频率分量的幅度表示原始时域信号中该分量的幅度或强度。 相反，相位表示该组件引入的时间偏移或延迟。 在数学上，与频率分量相关的复数可以表示为具有给定幅度和相位的复指数元素：

其中 $X(f)$是与频率 f 处的频率分量相关的复数，$\left|\begin{array}{c}X(f)\end{array}\right|$ 是分量的幅度，θ(f) 是分量的相位。 如图1（a）所示，在复平面中，复指数元素可以可视化为长度等于幅度、角度等于相位的向量：

因此，复频域中的复数提供了一种简洁而优雅的方式来表示傅里叶变换中每个频率分量的幅度和相位。

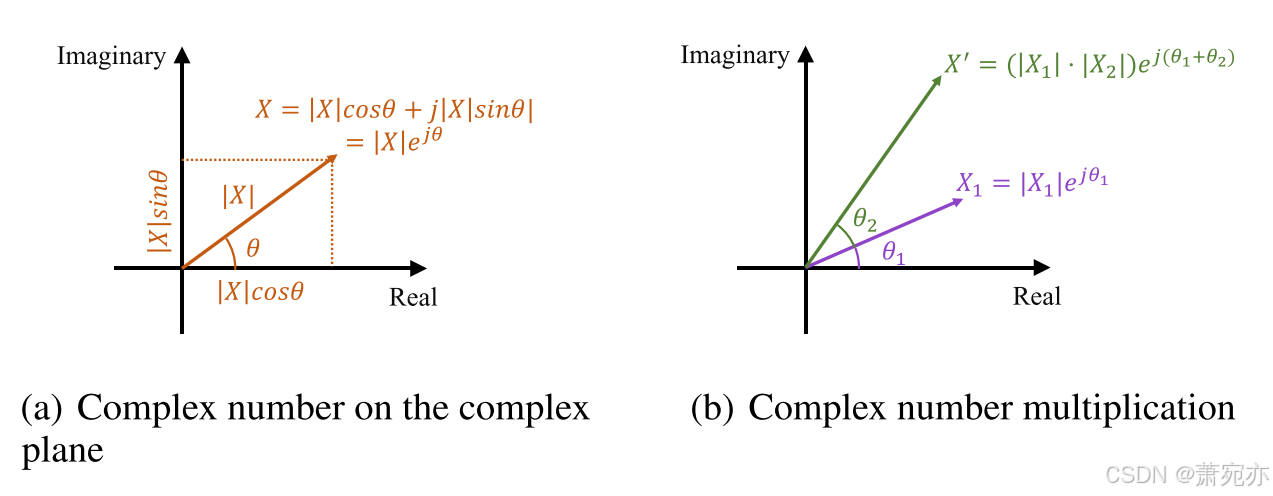
图 1：复数可视化和乘法说明

时移和相移。 信号的时移对应于频域中的相移。 特别是在复频域，我们可以通过将单位复指数元素乘以相应的相位来表示这种相移。 从数学上讲，如果我们将信号 x(t) 在时间上向前移动恒定量 τ，得到信号 $x(t-\tau )$，则傅里叶变换由下式给出：

移位后的信号仍具有 |X(f)| 的幅度，而相位${\theta }_{\tau }(f)=\theta (f)-2\pi f\tau$显示与时间移位呈线性关系的移位。

综上所述，幅度缩放和相移可以同时表示为复数的乘法，如图1（b）所示。

3.2 FITS PIPELINE

由于较长的时间序列在其频率表示中提供了更高的频率分辨率，我们训练 FITS 通过对输入时间序列段的频率表示进行插值来扩展时间序列段。 我们使用单层复值线性层来学习这种插值，这样它就可以在插值过程中学习幅度缩放和相移作为复数的乘法。 如图2所示，我们使用rFFT将时间序列段投影到复频域。 插值后，频率表示通过逆 rFFT (irFFT) 投影回来。

图 2：FITS 流程，重点是预测任务。 最初，时间序列被归一化为零均值，然后通过 rFFT 进行频域投影。 LPF 之后，单个复值线性层对频率进行插值。 然后，零填充和 irFFT 将其恢复到时域，而 iRIN 最终反转归一化。 除了重建监督损失之外，重建任务遵循相同的流程。 详细内容请查看附录。

然而，这些分段的平均值将导致其复杂频率表示中出现非常大的 0 频率分量。 为了解决这个问题，我们将其通过可逆实例标准化 (RIN)（Kim 等人，2022）以获得零均值实例。 因此，归一化复数频率表示现在的长度为 N/2，其中 N 表示时间序列的原始长度。

此外，FITS 还集成了低通滤波器 (LPF)，以进一步减小其模型尺寸。 LPF 有效地消除了高于指定截止频率的高频分量，压缩模型表示，同时保留基本的时间序列信息。 尽管在频域中运行，但 FITS 在时域中使用标准损失函数进行监督，例如实数到复数逆快速傅立叶变换 (irFFT) 后的均方误差 (MSE)。 这允许针对各种下游时间序列任务进行多功能监督。

在预测任务中，我们生成回溯窗口以及范围，如图 2 所示。这使我们能够为预测和回溯提供监督，鼓励模型准确地重建回溯窗口。 我们的消融研究表明，结合反向预测和预测监督可以在某些情况下提高性能。

对于重建任务，我们根据特定的下采样率对原始时间序列段进行下采样。 随后，采用 FITS 进行频率插值，使下采样片段重建回其原始形式。 因此，使用重建损失应用直接监督来确保忠实的重建。 重建任务也遵循图2中的流程，用重建损失代替监督。

3.3 KEY MECHANISMS OF FITS

复频率线性插值。 为了控制模型的输出长度，我们引入了一个插值率，表示为 η，它表示模型的输出长度 $L_o$与其对应的输入长度 $L_i$的比率。 频率插值对归一化的复频率表示进行操作，其长度是原始时间序列的一半。 重要的是，该插值率也可以应用于频域，如下式所示：

根据该公式，在任意频率f下，将原始信号中的频带1∼f线性投影到输出信号中的频带1∼ηf。 因此，我们将复值线性层的输入长度定义为 L，将插值输出长度定义为 ηL。 值得注意的是，当应用低通滤波器 (LPF) 时，L 的值对应于 LPF 的截止频率 (COF)。 执行频率插值后，复数频率表示被零填充到 Lo/2 的长度，其中 Lo 表示所需的输出长度。 在应用 irFFT 之前，引入一个额外的零作为表示的零频率分量。

低通滤波器 (LPF)。 将 LPF 合并到 FITS 中的主要目标是压缩模型的体积，同时保留基本信息。 LPF 通过丢弃高于指定截止频率 (COF) 的频率分量来实现此目的，从而获得更简洁的频域表示。 LPF保留时间序列中的相关信息，同时丢弃超出模型学习能力的成分。 这确保了原始时间序列有意义的内容的很大一部分被保留。 如图 3 所示，即使仅保留原始频域表示的四分之一，滤波后的波形也表现出最小的失真。 此外，LPF 滤除的高频分量通常包含噪声，这本质上与有效的时间序列建模无关。

图 3：从 ETTh1 数据集“OT”通道中选择的时间序列段的波形（第一行）和幅度谱（第二行），涵盖第 1500 个数据点到第 1980 个数据点。 该段的长度为 480，其主周期为 24，对应于基频 20。蓝线表示未应用滤波器的波形/频谱，而橙色线表示应用滤波器的波形/频谱。 滤波器截止频率是根据原始时间序列的谐波来选择的。

选择合适的截止频率 (COF) 仍然是一个不小的挑战。 为了解决这个问题，我们提出了一种基于主频率谐波含量的方法。 谐波是主频率的整数倍，在塑造时间序列波形方面发挥着重要作用。 通过将截止频率与这些谐波对齐，我们可以保留与信号结构和周期性相关的相关频率分量。 这种方法利用频率之间的固有关系来提取有意义的信息，同时抑制噪声和不相关的高频分量。 COF对不同谐波波形的影响如图3所示。我们在实验结果中进一步阐述了COF的影响。

重量共享。 FITS 通过共享权重（Zeng 等人，2023）来处理多变量任务，平衡性能和效率。 实际上，当源自同一物理系统时，通道通常共享一个公共基频，例如电器的 50/60Hz 或城市交通的日常基频。 我们实验中使用的大多数数据集都属于这一类。 对于确实包含不同基频通道的数据集，我们可以根据基频对这些通道进行聚类，并为每个聚类训练单独的 FITS 模型。

4 EXPERIMENTS FOR FORECASTING

4.1 FORECASTING AS FREQUENCY INTERPOLATION

通常，预测范围比给定的回溯窗口短，因此直接插值法不适合。 相反，我们将预测任务制定为将长度为 L 的回顾窗口插值到长度为 L+H 的回顾窗口和预测范围的组合。 这种设计使我们能够在培训期间提供更多的监督。 通过这种方法，我们不仅可以监督预测范围，还可以监督回溯窗口上的回溯任务。 我们的实验结果表明，这种独特的训练策略有助于提高 FITS 的表现。 预测任务的插值率计算公式为：

其中 L 代表回顾窗口的长度，H 代表预测范围的长度。

4.2 EXPERIMENT SETTINGS

数据集。 我们实验中使用的所有数据集都是广泛使用且公开的现实世界数据集，包括交通、电力、天气、ETT（Zhou et al., 2021）。 我们在附录中总结了这些数据集的特征。 除了这些用于长期时间序列预测的数据集外，我们还使用 M4 数据集来测试短期预测性能。 基线。 与最先进的时间序列预测模型相比，评估 FITS 的性能，包括 PatchTST (Nie et al., 2023)、TimesNet (Wu et al., 2023)、FEDFormer (Zhou et al., 2022a) ）和 LTSF-Linear（Zeng 等人，2023），我们使用官方实现 1 提供的代码和脚本重新运行所有实验。我们报告与 NBeats（Oreshkin 等人，2019）、NHits（Challu 等人）的比较 ., 2023）以及附录中其他基于变压器的方法。 评估指标。 我们遵循之前的工作（Zhou et al., 2022a；Zeng et al., 2023；Zhang et al., 2022），使用均方误差（MSE）作为核心指标来比较预测性能。 此外，为了评估短期预测，我们遵循 TimesNet（Wu 等人，2023）对称平均绝对百分比误差（SMAPE）。 实施细节。 我们对90、180、360、720的回溯窗口和唯一的超参数截止频率进行网格搜索。 进一步的实验还表明，在大多数情况下，较长的回顾窗口可以带来更好的性能。 为了避免信息泄漏，我们根据验证集的性能选择超参数。 我们将 FITS 的结果报告为随机选择的随机种子的 5 次运行的平均值和标准差。

4.3 COMPARISONS WITH SOTAS

Competitive Performance with High Efficiency
我们在表中展示了长期预测的实验结果。 1 和选项卡。 2. M4数据集的短期预测结果见附录。 值得注意的是，我们的 FITS 在所有实验中始终实现了可比甚至卓越的性能。 标签。 图 3 显示了在电力数据集上使用 96 的回顾窗口和 720 的预测范围的各种 TSF 模型的可训练参数和 MAC 2 的数量。 该表清楚地表明了 FITS 与其他模型相比的卓越效率。 在列出的模型中，参数数量从数百万到数千不等。 值得注意的是，TimesNet 和 Pyraformer 等大型模型需要的参数数量惊人，分别为 300.6M 和 241.4M。 同样，Informer、Autoformer 和 FEDformer 等流行模型的参数计数范围为 13.61M 到 20.68M。 即使是轻量级且最先进的模型 PatchTST 的参数数量也超过 100 万个。 相比之下，FITS 是一种高效模型，参数数量极少，因而脱颖而出。 与这些较大的模型相比，FITS 仅具有 4.5K 至 16K 参数，即可实现相当甚至更优越的性能。 值得强调的是，与第二小的模型 D线性（具有 139.7K 个参数）相比，FITS 需要的参数明显更少。 例如，当考虑 720 个回顾窗口和 720 个预测范围时，D线性模型需要超过 100 万个参数，而 FITS 只需 10k-50k 个参数即可实现类似的性能。

该分析展示了 FITS 的卓越效率。 尽管尺寸较小，但 FITS 始终取得有竞争力的结果，使其成为时间序列分析任务的有吸引​​力的选择。 FITS 表明，通过大幅减少参数占用量来实现最先进或接近最先进的性能是可能的，使其成为资源受限环境的理想选择。

Case Study on ETTh2 Dataset

我们使用 ETTh2 数据集对 FITS 的性能进行了全面的案例研究，进一步凸显了回溯窗口和截止频率对模型性能的影响。 我们在附录中提供了有关其他数据集的案例研究。 在我们的实验中，我们观察到增加回顾窗口通常会提高性能，而增加截止频率的效果很小。

标签。 图 4 显示了使用不同回溯窗口大小和截止频率获得的性能结果。 较大的回顾窗口往往会产生更好的整体性能。 另一方面，增加截止频率只会带来边际性能改进。 然而，值得注意的是，更高的截止频率是以增加计算资源为代价的，如表 1 所示。 5.

考虑到这些观察结果，我们发现利用较长的回顾窗口与低截止频率相结合，可以以最小的计算成本实现接近最先进的性能。 例如，当采用 720 回溯窗口并将截止频率设置为二次谐波时，FITS 优于其他方法。 值得注意的是，FITS 凭借仅约 10k 的参数数量就实现了最先进的性能。 此外，通过将回顾窗口减少到 360，FITS 通过将截止频率设置为二次谐波，已经实现了接近最先进的性能，从而将模型的参数数量进一步减少到 5k 以下 （如表5所示）。

这些结果强调了 FITS 的轻量级性质，使其非常适合在计算资源有限的边缘设备上进行部署和训练。 通过仔细选择回溯窗口和截止频率，FITS 可以在保持计算效率的同时实现出色的性能，使其成为现实应用程序的有吸引力的选择。

5 EXPERIMENT FOR ANOMALY DETECTION

5.1 RECONSTRUCTION AS FREQUENCY INTERPOLATION

如前所述，我们用自监督重建方法来处理异常检测任务。 具体来说，我们对输入进行 N 次等距采样，并训练插值率为 ηRec = N 的 FITS 网络对其进行上采样。 详情请参阅附录 A。

5.2 EXPERIMENT SETTINGS

数据集。 我们使用五个常用的基准数据集：SMD（服务器机器数据集（Su et al., 2019））、PSM（轮询服务器指标（Abdulaal et al., 2021））、SWaT（安全水处理（Mathur & Tippenhauer, 2016）） ）、MSL（火星科学实验室漫游车）和 SMAP（土壤湿度主动被动卫星）（Hundman 等，2018）。 我们在附录 F. 基线中报告了合成数据集（Lai 等人，2021）的性能。 我们将 FITS 与 TimesNet (Wu et al., 2023)、Anomaly Transformer (Xu et al., 2022)、THOC (Shen et al., 2020)、Omnianomaly (Su et al., 2019)、DGHL (Su et al., 2019) 等模型进行比较。 Challu 等人，2022b)。 继TimesNet（Wu et al., 2023）之后，我们还将异常检测性能与其他模型进行了比较（Zeng et al., 2023；Zhang et al., 2022；Woo et al., 2022；Zhou et al., 2022a） 。 评估指标。 继之前的工作（Xu et al., 2022；Shen et al., 2020；Wu et al., 2023）之后，我们使用 Precision、Recall 和 F1-score 作为指标。

实施细节。 我们使用 200 的窗口大小，并将时间序列段下采样 4 倍，作为训练 FITS 的输入来重建原始段。 我们遵循 Anomaly Transformer (Xu et al., 2022) 的方法，其中超过特定​​重建损失阈值的时间点被归类为异常。 阈值是根据验证集上获得的最高 F1 分数选择的。 为了处理连续异常段，我们采用了广泛使用的调整策略（Su et al., 2019; Xu et al., 2018; Shen et al., 2020），考虑到特定连续异常段内的所有异常在以下情况下均被正确检测到： 识别出一个异常时间点。 这种方法符合现实世界的应用，其中异常时间点通常会引发对整个细分市场的关注。

5.3 COMPARISONS WITH SOTAS

在表 6 中，FITS 在各种数据集上都取得了出色的结果。 特别是在 SMD 和 SWaT 数据集上，FITS 实现了近乎完美的 F1 分数，分别约为 99.95% 和 98.9%，展示了其在异常检测和分类方面的精度。 相比之下，TimesNet、Anomaly Transformer 和 Stationary Transformer 等模型在这些数据集上的性能很难与 FITS 相匹配。 然而，FITS 在 SMAP 和 MSL 数据集上的性能相对较低。 这些数据集由于其二进制事件数据性质而提出了挑战，FITS 的频域表示可能无法有效捕获这些数据。 在这种情况下，时域建模是更可取的，因为原始数据格式足够紧凑。 因此，专门为异常检测而设计的模型（例如 THOC 和 Omni Anomaly）在这些数据集上获得了更高的 F1 分数。 为了进行更全面的评估，可以在附录中找到波形可视化和详细分析，从而更深入地了解 FITS 在不同异常检测场景中的优势和局限性。 值得注意的是，报告的结果是在参数范围为 1-4K 和 MAC（乘法累加运算）为 10-137K 的情况下实现的，这将在附录中进一步详细说明。

虽然正在使用的数据集很有用，但必须承认它们的局限性（Lai 等人，2021）中所述。 特别是在（Lai 等人，2021）的合成数据集上，FITS 展示了无可挑剔的检测能力，获得了完美的 100% F1 分数。 详细的细分，读者可以参考附录F中的表格。该数据集将单频正弦波与复杂引入的异常模式结合在一起，这对时域识别提出了挑战。 然而，FITS 利用频域，能够熟练地识别这些异常，特别是那些引入意外频率分量的异常。 此外，FITS 拥有令人印象深刻的亚毫秒级推理速度——与较大模型或通信开销的典型延迟相比，这是一个显着的区别。 这一速度凸显了 FITS 作为快速发现关键错误的急救工具的适用性。 当作为初步过滤器与专门用于详细检测的 AD 算法配对时，组合系统成为面对各种异常情况时稳健性和快速响应能力的典范。

6 CONCLUSIONS AND FUTURE WORK

在本文中，我们提出了用于时间序列分析的 FITS，这是一种具有 10k 参数的低成本模型，其性能可以与通常大几个数量级的最先进模型相媲美。 作为未来的工作，我们计划在更真实的场景中评估 FITS 并提高其可解释性。 此外，我们还旨在探索频域大规模复值神经网络，例如复值 Transformer。

---