《人工智能》实验二——搜索技术（八数码问题）

最新推荐文章于 2023-03-09 11:29:18 发布
最新推荐文章于 2023-03-09 11:29:18 发布
阅读量8.5k 收藏 133
点赞数 20
分类专栏： 人工智能实验 文章标签： 人工智能
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_45884316/article/details/120978957
版权

在这里插入图片描述

  • 必须记住下一步还可以走哪些点——OPEN表（记录还没有扩展的点）
  • 必须记住哪些点走过了——CLOSED表（记录已经扩展的点
    在这里插入图片描述

在这里插入图片描述

广度优先搜索

在应用BFS算法进行八数码问题搜索时需要open和closed两个表。首先将初始状态加入open队列，然后进行出队操作并放入closed中，对出队的状态进行扩展（所谓扩展也就是找出其上下左右移动后的状态），将扩展出的状态加入队列，然后继续循环出队-扩展-入队的操作，直到找到解为止。
在这里插入图片描述

import copy
#棋盘的类，实现移动和扩展状态
class grid:
    def __init__(self,stat):
        self.pre=None
        self.target=[[1,2,3],[8,0,4],[7,6,5]]
        self.stat=stat
        self.find0()
        self.update()
    #更新深度和距离和
    def update(self):
        self.fH()
        self.fG()
    #G是深度，也就是走的步数
    def fG(self):
        if(self.pre!=None):
            self.G=self.pre.G+1
        else:
            self.G=0
    #H是和目标状态距离之和，可以用来判断是否达到最优解
    def fH(self):
        self.H=0
        for i in range(3):
            for j in range(3):
                targetX=self.target[i][j]
                nowP=self.findx(targetX)
                self.H+=abs(nowP[0]-i)+abs(nowP[1]-j)
    #查看当前状态
    def see(self):
        print("depth：",self.G)
        for i in range(3):
             print(self.stat[i])
        print("-"*10)
    #查看找到的解是如何从头移动的
    def seeAns(self):
        ans=[]
        ans.append(self)
        p=self.pre
        while(p):
            ans.append(p)
            p=p.pre
        ans.reverse()
        for i in ans:
            i.see()
    #找到数字x的位置，返回其坐标
    def findx(self,x):
        for i in range(3):
            if(x in self.stat[i]):
                j=self.stat[i].index(x)
                return [i,j]
    #找到0，也就是空白格的位置
    def find0(self):
            self.zero=self.findx(0)
    #对当前状态进行所有可能的扩展，返回一个扩展状态的列表
    def expand(self):
        i=self.zero[0]
        j=self.zero[1]
        gridList=[]

        if(j==2 or j==1):
            gridList.append(self.left())
        if(i==2 or i==1):
            gridList.append(self.up())
        if(i==0 or i==1):
            gridList.append(self.down())
        if(j==0 or j==1):
            gridList.append(self.right())

        return gridList


    #deepcopy多维列表的复制，防止指针赋值将原列表改变
    #move只能移动行或列，即row和col必有一个为0
    #对当前状态进行移动
    def move(self,row,col):
        newStat=copy.deepcopy(self.stat)
        tmp=self.stat[self.zero[0]+row][self.zero[1]+col]
        newStat[self.zero[0]][self.zero[1]]=tmp
        newStat[self.zero[0]+row][self.zero[1]+col]=0
        return newStat

    def up(self):
        return self.move(-1,0)

    def down(self):
        return self.move(1,0)

    def left(self):
        return self.move(0,-1)

    def right(self):
        return self.move(0,1)


#计算逆序数之和
def N(nums):
    N=0
    for i in range(len(nums)):
        if(nums[i]!=0):
            for j in range(i):
                if(nums[j]>nums[i]):
                    N+=1
    return N

#根据逆序数之和判断所给八数码是否可解
def judge(src,target):
    N1=N(src)
    N2=N(target)
    if(N1%2==N2%2):
        return True
    else:
        return False

#初始化状态
startStat=[[2,8,3],[1,0,4],[7,6,5]]
g=grid(startStat)
if(judge(startStat,g.target)!=True):
    print("所给八数码无解，请检查输入")
    exit(1)

visited=[]
queue=[g]
time=0
while(queue):
    time+=1
    v=queue.pop(0)
    #判断是否找到解
    if(v.H==0):
        print("found and times:",time,"moves:",v.G)
        #查看找到的解是如何从头移动的
        v.seeAns()
        break
    else:
        #对当前状态进行扩展
        visited.append(v.stat)
        expandStats=v.expand()
        for stat in expandStats:
            tmpG=grid(stat)
            tmpG.pre=v
            tmpG.update()
            if(stat not in visited):
                queue.append(tmpG)

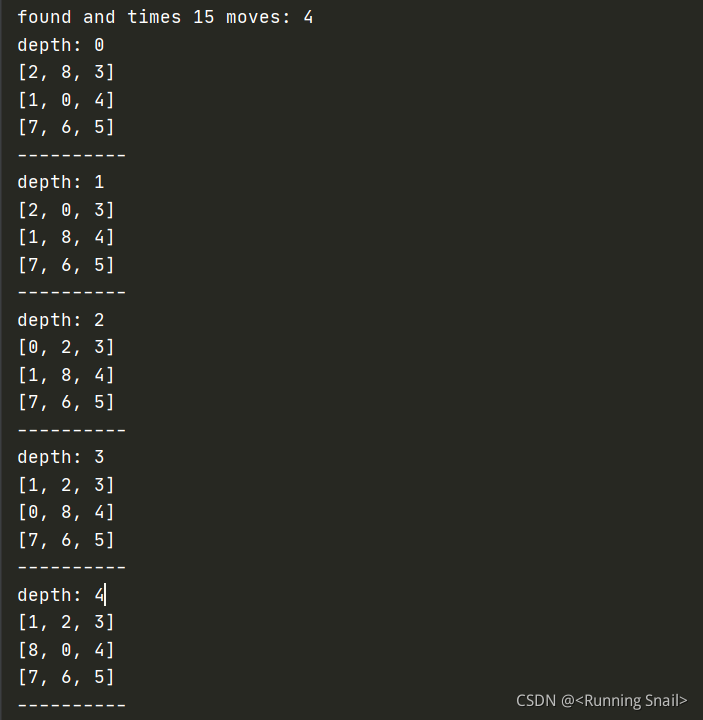
在这里插入图片描述

深度优先搜索

在这里插入图片描述

# -*- coding: utf-8 -*-

'''
深度优先搜索实现
'''


import copy
#棋盘的类，实现移动和扩展状态
class grid:
    def __init__(self, stat):
        self.pre = None
        self.target = [[1, 2, 3], [8, 0, 4], [7, 6, 5]]
        self.stat = stat
        self.find0()
        self.update()
    #更新深度和距离和
    def update(self):
        self.fH()
        self.fG()

    # G是深度，也就是走的步数
    def fG(self):
        if (self.pre != None):
            self.G = self.pre.G + 1
        else:
            self.G = 0

    # H是和目标状态距离之和，可以用来判断是否找到解
    def fH(self):

        self.H = 0
        for i in range(3):
            for j in range(3):
                targetX = self.target[i][j]
                nowP = self.findx(targetX)
                self.H += abs(nowP[0] - i) + abs(nowP[1] - j)

    #以三行三列的形式输出当前状态
    def see(self):
        print("depth:", self.G)
        for i in range(3):
            print(self.stat[i])
        print("-" * 10)

    # 查看找到的解是如何从头移动的
    def seeAns(self):
        ans = []
        ans.append(self)
        p = self.pre
        while (p):
            ans.append(p)
            p = p.pre
        ans.reverse()
        for i in ans:
            i.see()
    #找到数字x的位置
    def findx(self, x):
        for i in range(3):
            if (x in self.stat[i]):
                j = self.stat[i].index(x)
                return [i, j]
    #找到0的位置，也就是空白格的位置
    def find0(self):
        self.zero = self.findx(0)

    #对当前状态进行扩展，也就是上下左右移动，返回的列表中是状态的二维列表，不是对象
    def expand(self):
        i = self.zero[0]
        j = self.zero[1]
        gridList = []
        if (j == 2 or j == 1):
            gridList.append(self.left())
        if (i == 2 or i == 1):
            gridList.append(self.up())
        if (i == 0 or i == 1):
            gridList.append(self.down())
        if (j == 0 or j == 1):
            gridList.append(self.right())
        return gridList

    # deepcopy多维列表的复制，防止指针赋值将原列表改变
    # move只能移动行或列，即row和col必有一个为0
    #对当前状态进行移动的函数
    def move(self, row, col):
        newStat = copy.deepcopy(self.stat)
        tmp = self.stat[self.zero[0] + row][self.zero[1] + col]
        newStat[self.zero[0]][self.zero[1]] = tmp
        newStat[self.zero[0] + row][self.zero[1] + col] = 0
        return newStat

    def up(self):
        return self.move(-1, 0)

    def down(self):
        return self.move(1, 0)

    def left(self):
        return self.move(0, -1)

    def right(self):
        return self.move(0, 1)

# 判断状态g是否在状态集合中，g是对象，gList是对象列表
#返回的结果是一个列表，第一个值是真假，如果是真则第二个值是g在gList中的位置索引
def isin(g, gList):
    gstat = g.stat
    statList = []
    for i in gList:
        statList.append(i.stat)
    if (gstat in statList):
        res = [True, statList.index(gstat)]
    else:
        res = [False, 0]
    return res

#计算逆序数之和
def N(nums):
    N=0
    for i in range(len(nums)):
        if(nums[i]!=0):
            for j in range(i):
                if(nums[j]>nums[i]):
                    N+=1
    return N

#根据逆序数之和判断所给八数码是否可解
def judge(src,target):
    N1=N(src)
    N2=N(target)
    if(N1%2==N2%2):
        return True
    else:
        return False

#初始状态
startStat = [[2, 8, 3], [1, 0, 4], [7, 6, 5]]
g = grid(startStat)
#判断所给的八数码受否有解
if(judge(startStat,g.target)!=True):
    print("所给八数码无解，请检查输入")
    exit(1)
#visited储存的是已经扩展过的节点
visited = []
time = 0
#用递归的方式进行DFS遍历
def DFSUtil(v, visited):
    global time
    #判断是否达到深度界限
    if (v.G > 4):
        return
    time+=1
    #判断是否已经找到解
    if (v.H == 0):
        print("found and times", time, "moves:", v.G)
        v.seeAns()
        exit(1)

    #对当前节点进行扩展
    visited.append(v.stat)
    expandStats = v.expand()
    w = []
    for stat in expandStats:
        tmpG = grid(stat)
        tmpG.pre = v
        tmpG.update()
        if (stat not in visited):
            w.append(tmpG)
    for vadj in w:
        DFSUtil(vadj, visited)
    #visited查重只对一条路，不是全局的，每条路开始时都为空
    #因为如果全局查重，会导致例如某条路在第100层找到的状态，在另一条路是第2层找到也会被当做重复
    #进而导致明明可能会找到解的路被放弃
    visited.pop()

DFSUtil(g, visited)
#如果找到解程序会在中途退出，走到下面这一步证明没有找到解
print("在当前深度下没有找到解，请尝试增加搜索深度")

在这里插入图片描述

3. 启发式搜索

特点：重排OPEN表，选择最有希望的节点加以扩展。

引入估价函数(evaluation function)来估计节点位于解路径上的“希望”，函数值越小“希望”越大 搜索过程中按照估价函数的大小对OPEN表排序, 每次选择估价函数值最小的节点作为下一步考察的节点

3.1 有序搜索

选择OPEN表上具有最小f 值的节点作为下一个要扩展的节点。

在这里插入图片描述
对应到八数码问题：
f ( x ) = g ( x ) + h ( x ) f (x) = g (x) + h (x) f(x)=g(x)+h(x)

  • g (x)：从初始状态到x需要进行的移动操作的次数
  • h (x)：所有棋子与目标位置的曼哈顿距离之和
    • 曼哈顿距离：两点之间水平距离和垂直距离之和 仍满足估价函数的限制条件
'''
有序搜索
'''


import copy
import numpy as np
from datetime import datetime


# 字符串列表化
def string_to_ls(str):
    return [i.split(' ') for i in str.split(',')]


# 获取位置
def get_loacl(arr, target):
    # r, c = np.where(arr == target)
    # return r, c
    for i in arr:
        for j in i:
            if j == target:
                return arr.index(i), i.index(j)


# 获取可以和0交换位置的元素
def get_elements(arr):
    r, c = get_loacl(arr, '0')
    elements = []
    if r > 0:
        elements.append(arr[r - 1][c])  # 上面的元素
    if r < 2:
        elements.append(arr[r + 1][c])  # 下边的元素
    if c > 0:
        elements.append(arr[r][c - 1])  # 左面的元素
    if c < 2:
        elements.append(arr[r][c + 1])  # 右面的元素
    return elements


def get_child(arr, e):
    # 深拷贝与浅拷贝！!
    arr_new = copy.deepcopy(arr)
    r, c = get_loacl(arr_new, '0')
    r1, c1 = get_loacl(arr_new, e)
    arr_new[r][c], arr_new[r1][c1] = arr_new[r1][c1], arr_new[r][c]
    return arr_new


# 哈密尔顿距离
def get_distance(arr1, arr2):
    distance = []
    for i in arr1:
        for j in i:
            loc1 = get_loacl(arr1, j)
            loc2 = get_loacl(arr2, j)
            distance.append(abs(loc1[0] - loc2[0]) + abs(loc1[1] - loc2[1]))
    return sum(distance)


def is_goal(arr, goal):
    return arr == goal


class state:
    def __init__(self, state, deep, parent, distance):
        # state是一个3x3的ls矩阵
        self.state = state
        self.deep = deep
        self.parent = parent
        self.distance = distance

    def chidren(self):
        chidren = []
        for i in get_elements(self.state):
            child = state(state=get_child(self.state, i),
                          deep=self.deep + 1,
                          parent=self,
                          distance=self.deep + 1 + get_distance(self.state, goal_arr))
            chidren.append(child)
        return chidren


# 打印求解路径
def print_path(n):
    if n.parent == None:
        return
    else:
        print('↑')
        print(np.array(n.parent.state))
        print_path(n.parent)


if __name__ == '__main__':
    # initial = '0 1 3,4 2 5,7 8 6'
    # goal = '4 1 3,7 0 5,8 2 6'
    initial = '4 0 1,6 8 5,7 3 2'
    goal = '5 8 2,1 0 4,6 3 7'
    initial_arr = string_to_ls(initial)
    goal_arr = string_to_ls(goal)
    initial_arr = state(initial_arr, deep=0, parent=None, distance=get_distance(initial_arr, goal_arr))
    start = datetime.now()
    open = [initial_arr]
    close = []
    # limit = eval(input('请输入要搜索的深度：'))
    limit = 19
    while len(open) > 0:
        open_tb = [i.state for i in open]
        close_tb = [i.state for i in close]
        n = open.pop(0)
        close.append(n)
        if is_goal(n.state, goal_arr):
            print(np.array(n.state))
            print_path(n)
            print('--' * 20)
            print('成功搜索到路径，求解过程如上')
            break
        else:
            if n.deep < limit:
                for i in n.chidren():
                    if i.state not in open_tb:
                        if i.state not in close_tb:
                            open.insert(0, i)
                            open.sort(key=lambda x: x.distance)
    else:
        print('该深度下无解')

    end = datetime.now()
    print('--' * 20)
    print('限制深度为：{}\t搜寻深度为：{}\n启发式A算法搜索步数为：{}'.format(limit, close[-1].deep, len(close) - 2))
    print('--' * 20)
    print('搜索耗时:', end - start)

在这里插入图片描述

3.2 A*算法

估价函数的定义
对节点n定义 f ∗ ( n ) = g ∗ ( n ) + h ∗ ( n ) f ^*(n)=g^ *(n)+h^*(n) f∗(n)=g∗(n)+h∗(n),表示从S开始约束通过节点n的一条最佳路径的代价。希望估价函数f 定义为：f(n)=g(n)+h(n)，g是g的估计 ，h是h的估计

A算法的定义
定义1 在GRAPHSEARCH过程中，如果第8步的重排OPEN表是依据f(x)=g(x)+h(x)进行的，则称该过程为A算法。
定义2 在A算法中，如果对所有的x存在h(x)≤h(x),则称h(x)为h*(x)的下界，它表示某种偏于保守的估计。
定义3 采用h*(x)的下界h(x)为启发函数的A算法，称为A算法。当h=0时， A算法就变为有序搜索算法。

在这里插入图片描述

import copy
#棋盘的类，实现移动和扩展状态
class grid:
    def __init__(self,stat):
        self.pre=None
        #目标状态
        self.target=[[1,2,3],[8,0,4],[7,6,5]]
        #stat是一个二维列表
        self.stat=stat
        self.find0()
        self.update()
    #更新启发函数的相关信息
    def update(self):
        self.fH()
        self.fG()
        self.fF()

    #G是深度，也就是走的步数
    def fG(self):
        if(self.pre!=None):
            self.G=self.pre.G+1
        else:
            self.G=0

    #H是和目标状态距离之和
    def fH(self):
        self.H=0
        for i in range(3):
            for j in range(3):
                targetX=self.target[i][j]
                nowP=self.findx(targetX)
                #曼哈顿距离之和
                self.H+=abs(nowP[0]-i)+abs(nowP[1]-j)

    #F是启发函数，F=G+H
    def fF(self):
        self.F=self.G+self.H

    #以三行三列的形式输出当前状态
    def see(self):
        for i in range(3):
             print(self.stat[i])
        print("F=",self.F,"G=",self.G,"H=",self.H)
        print("-"*10)

    #查看找到的解是如何从头移动的
    def seeAns(self):
        ans=[]
        ans.append(self)
        p=self.pre
        while(p):
            ans.append(p)
            p=p.pre
        ans.reverse()
        for i in ans:
            i.see()

    #找到数字x的位置
    def findx(self,x):
        for i in range(3):
            if(x in self.stat[i]):
                j=self.stat[i].index(x)
                return [i,j]

    #找到0，也就是空白格的位置
    def find0(self):
            self.zero=self.findx(0)

    #扩展当前状态，也就是上下左右移动。返回的是一个状态列表，也就是包含stat的列表
    def expand(self):
        i=self.zero[0]
        j=self.zero[1]
        gridList=[]
        if(j==2 or j==1):
            gridList.append(self.left())
        if(i==2 or i==1):
            gridList.append(self.up())
        if(i==0 or i==1):
            gridList.append(self.down())
        if(j==0 or j==1):
            gridList.append(self.right())
        return gridList


    #deepcopy多维列表的复制，防止指针赋值将原列表改变
    #move只能移动行或列，即row和col必有一个为0
    #向某个方向移动
    def move(self,row,col):
        newStat=copy.deepcopy(self.stat)
        tmp=self.stat[self.zero[0]+row][self.zero[1]+col]
        newStat[self.zero[0]][self.zero[1]]=tmp
        newStat[self.zero[0]+row][self.zero[1]+col]=0
        return newStat

    def up(self):
        return self.move(-1,0)

    def down(self):
        return self.move(1,0)

    def left(self):
        return self.move(0,-1)

    def right(self):
        return self.move(0,1)

#判断状态g是否在状态集合中，g是对象，gList是对象列表
#返回的结果是一个列表，第一个值是真假，如果是真则第二个值是g在gList中的位置索引
def isin(g,gList):
    gstat=g.stat
    statList=[]
    for i in gList:
        statList.append(i.stat)
    if(gstat in statList):
        res=[True,statList.index(gstat)]
    else:
        res=[False,0]
    return res

#计算逆序数之和
def N(nums):
    N=0
    for i in range(len(nums)):
        if(nums[i]!=0):
            for j in range(i):
                if(nums[j]>nums[i]):
                    N+=1
    return N

#根据逆序数之和判断所给八数码是否可解
def judge(src,target):
    N1=N(src)
    N2=N(target)
    if(N1%2==N2%2):
        return True
    else:
        return False

#Astar算法的函数
def Astar(startStat):
    #open和closed存的是grid对象
    open=[]
    closed=[]
    #初始化状态
    g=grid(startStat)
    #检查是否有解
    if(judge(startStat,g.target)!=True):
        print("所给八数码无解，请检查输入")
        exit(1)

    open.append(g)
    #time变量用于记录遍历次数
    time=0
    #当open表非空时进行遍历
    while(open):
        #根据启发函数值对open进行排序，默认升序
        open.sort(key=lambda G:G.F)
        #找出启发函数值最小的进行扩展
        minFStat=open[0]
        #检查是否找到解，如果找到则从头输出移动步骤
        if(minFStat.H==0):
            print("found and times:",time,"moves:",minFStat.G)
            minFStat.seeAns()
            break

        #走到这里证明还没有找到解，对启发函数值最小的进行扩展
        open.pop(0)
        closed.append(minFStat)
        expandStats=minFStat.expand()
        #遍历扩展出来的状态
        for stat in expandStats:
            #将扩展出来的状态（二维列表）实例化为grid对象
            tmpG=grid(stat)
            #指针指向父节点
            tmpG.pre=minFStat
            #初始化时没有pre，所以G初始化时都是0
            #在设置pre之后应该更新G和F
            tmpG.update()
            #查看扩展出的状态是否已经存在与open或closed中
            findstat=isin(tmpG,open)
            findstat2=isin(tmpG,closed)
            #在closed中,判断是否更新
            if(findstat2[0]==True and tmpG.F<closed[findstat2[1]].F):
                closed[findstat2[1]]=tmpG
                open.append(tmpG)
                time+=1
            #在open中，判断是否更新
            if(findstat[0]==True and tmpG.F<open[findstat[1]].F):
                open[findstat[1]]=tmpG
                time+=1
            #tmpG状态不在open中，也不在closed中
            if(findstat[0]==False and findstat2[0]==False):
                open.append(tmpG)
                time+=1

stat=[[2, 8, 3], [1, 0 ,4], [7, 6, 5]]
Astar(stat)

在这里插入图片描述

https://github.com/roadwide/AI-Homework

https://blog.csdn.net/Juuunn/article/details/109439359

八数码问题
bugster的博客
06-04 2635
状态空间法表示 ①建立一个只含有初始节点s0的搜索图g，把s0放入open表中 ②建立closed表，且置为空表 ③判断open表是否为空表，若为空，则问题无解，退出...
人工智能导论（5-9）-TYUT
weixin_51603782的博客
05-06 8534
考前复习
人工智能----八数码难题解决 原理及算法实现
热门推荐
墨轩
11-25 1万+
1．启发式搜索算法A 启发式搜索算法A，一般简称为A算法，是一种典型的启发式搜索算法。其基本思想是：定义一个评价函数f，对当前的搜索状态进行评估，找出一个最有希望的节点来扩展。 评价函数的形式如下： f(n)＝g(n)＋h(n) 其中n是被评价的节点。 f(n)、g(n)和h(n)各自表述什么含义呢？我们先来定义下面几个函数的含义，它们与f(n)、g(n)和h(n)的差别是都带有一个“*...
人工智能实验——八数码问题网页可视化
07-07
在本项目中，我们主要探讨的是“人工智能实验——八数码问题网页可视化”。八数码问题，又称滑块拼图，是一个经典的计算机科学问题，它属于图灵完全问题，且与人工智能中的搜索算法紧密相关。这个实验的目标是通过...
AI实验1——八数码问题
weixin_45607056的博客
10-25 2951
AI实验1——八数码问题 一、实验目的与要求 实验目的： 1 . 熟悉状态空间表示法； 2．掌握深度优先、广度优先和等代价无信息搜索算法； 3．掌握启发式函数设计，实现面向实际问题的A*搜索算法； 二、实验内容与方法 实验内容： 利用无信息搜索算法实现八数码难题求解； 设计启发式信息函数，利用A*搜索实现八数码难题求解； 三、实验步骤与过程 1,问题分析 在八数码难题中，我们使用状态空间表示法，将八数码矩阵（即矩阵的状态）设置为一个节点类（Node），各个节点之间通过操作集（Operater）[‘U
新实验三 人工智能之八数码问题 A星算法.rar
01-19
《人工智能之八数码问题与A*算法解析》 在信息技术高速发展的今天，人工智能（AI）已经深入到我们生活的各个领域。作为AI中的一个重要课题，八数码问题（又称滑动拼图游戏）是一个经典的搜索问题，它能很好地展示...
人工智能实验三-15数码问题实现
最新发布
03-30
人工智能实验三——15数码问题实现 1实验内容 15数码问题实现: 1、任选语言，采用A*算法实现问题求解，并给出具体的移动步骤 2、尝试设计不同的启发式函数h，并分析对结果的影响 2 实验目的 通过人工智能实验，...
代价树的广度优先搜索 带有open表和closed表的显示
04-24
代价树的广度优先搜索 带有open表和closed表的显示
图搜索与问题求解 图搜索与问题求解
03-11
3.1 状态图搜索 3.2 状态图搜索问题求解 3.3 与或图搜索 3.4 与或图搜索问题求解
人工智能 八数码问题
07-29
人工智能中基本问题，利用VC解决八数码问题。利用了宽度优先搜索和广度优先搜索。
用深度优先、广度优先算法解决八数码问题
09-29
网上大部分解决8数码问题都只采用宽度优先算法。我在宽度优先的基础上，设计出深度优先算法。并制作出界面，方便输入、输出。希望能对学习相关内容的同志有所帮助
八数码问题实验报告1
08-03
本实验主要涉及的是在人工智能领域中的一种经典问题——八数码问题，使用C++编程语言实现A*算法进行求解。A*算法是一种启发式搜索算法，它结合了实际走过的代价（g(n)）和预估到目标的代价（h(n)），形成综合评价...
人工智能-求解八数码问题
lbx0815的博客
07-02 2904
2.3 算法伪代码首先定义两个表，open表用于存放已经生成，且已用启发式函数进行过估计或评价，但尚未产生它们的后继节点的那些结点，这些结点也称未考察结点；closed表用于存放已经生成，且已考察过的结点。设S0为初态，Sg为目标状态。具体过程如下：(1) 把S0放入open表，记为f=h，令closed为空表；(2)重复下列过程，直至找到目标结点为止。若open为空表，则失败；(3)选取open...
A/A*算法解决八数码问题（C++实现）
weixin_44735393的博客
01-17 6920
@A算法解决八数码问题 一、实验原理 1.状态图搜索 1.1搜索树：搜索过程中经过的节点和边按原图的连接关系构成一个树型的有向图，称为搜索树。 1.2搜索方式 树式搜索：记录搜索过程中所经过的所有节点和边 1.3路径的获得 树式搜索：反向求解 2.搜索算法 2.1 CLOSED表和OPEN表 closed表对树式搜索来说存储的是正在成长的搜索树，对线式搜索来说存储的是不断伸长的折线，本身就是所求的...
八数码难题——启发算法
hongshanqu的博客
03-09 1106
因为每个节点都有一个启发值属性，需把启发值和节点一同放入open表，所以管理open表的方式略有不同，这里定义了一个新的expand_new函数管理open。还有，open表也不再按先进先出或后进先出的原则弹出节点，而是按启发值大小弹出节点。此外还需要定义一个按启发值大小弹出节点的新函数pop。启发算法和盲目搜索算法，同样需要open表和closed表，最大的不同之处是：每个节点有一个启发值，然后优先搜索启发值小的节点。代码在前面盲目搜索（带路径的）的基础编写，加入启发函数部分。需要移动 25 步,
八数码问题的人工智能实验分析与代码实现
文件信息表明，该资源是一份针对人工智能领域中的经典搜索问题——八数码问题的实验性代码和研究论文。通过对八数码问题的解决，可以深入理解搜索算法的原理及其在解决人工智能问题中的应用。同时，该研究可能为搜索...
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值