引言
\qquad 生活中有很多物理现象都是连续的,例如温度随时间的变化、汽车位移随时间的变化。其实数学中的连续性与之类似。这一节就来研究一下数学中的连续。
连续性定义
定义 1 如果 lim x → a f ( x ) = f ( a ) \lim_{x \rightarrow a}f(x) = f(a) limx→af(x)=f(a),函数 f f f在 x = a x = a x=a处连续。
从上面的定义,可以看出函数 f f f要在 a a a处连续,需要满足三个条件:
- f ( a ) f(a) f(a)存在(即 a a a在函数 f f f的定义域内)
- lim x → a f ( x ) \lim_{x \rightarrow a}f(x) limx→af(x)存在
- lim x → a f ( x ) = f ( a ) \lim_{x \rightarrow a}f(x) = f(a) limx→af(x)=f(a)
从几何角度上来说,如果一个函数的图像在某个区间内没有间断,那么这个函数在该区间内就是连续的。
例一:根据定义 1再结合函数的图像,说明函数在哪些点上不连续。
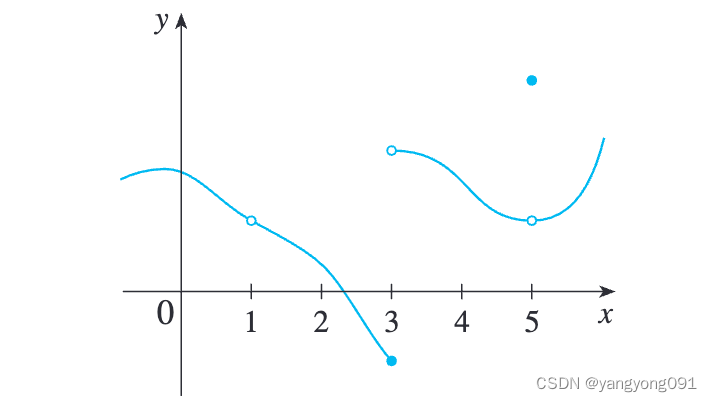
解:
- 函数在 x = 1 x = 1 x=1处不连续,因为 f ( 1 ) f(1) f(1)不存在;
- 函数在 x = 3 x = 3 x=3处不连续,因为 lim x → 3 f ( x ) \lim_{x \rightarrow 3}f(x) limx→3f(x)不存在;
- 函数在 x = 5 x = 5 x=5处不连续,因为 lim x → 5 f ( x ) ≠ f ( 5 ) \lim_{x \rightarrow 5}f(x) \neq f(5) limx→5f(x)=f(5)。
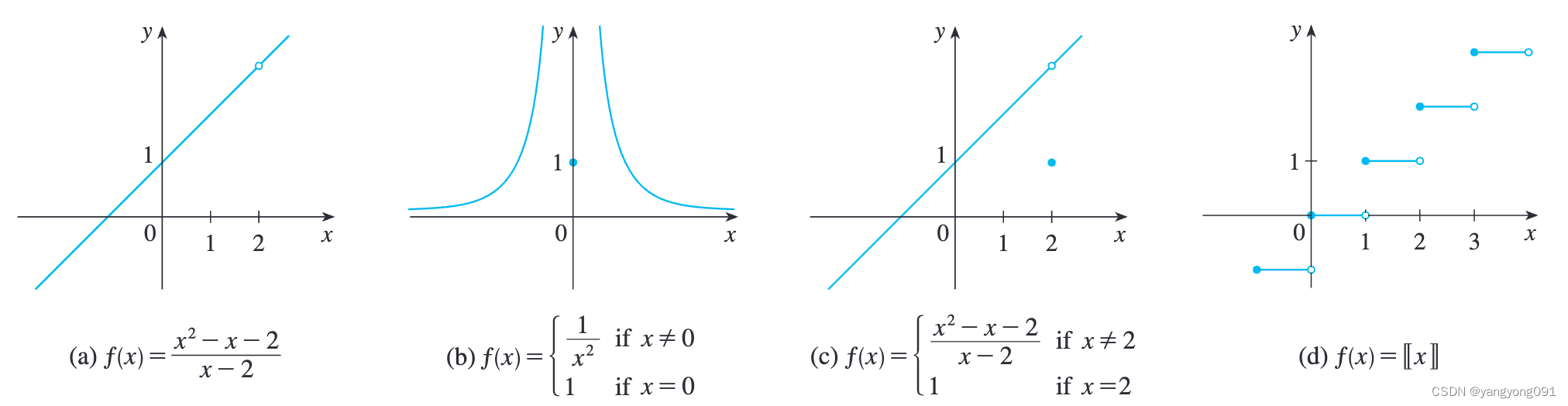
例二:找出下列函数不连续的点。
(a)
f
(
x
)
=
x
2
−
x
−
2
x
−
2
f(x) = \frac{x^2 - x - 2}{x - 2}
f(x)=x−2x2−x−2
(b)
f
(
x
)
=
{
1
x
2
x
≠
1
1
x
=
1
f(x)=\left\{ \begin{aligned} & \frac{1}{x^2} & x \neq 1\\ & 1 & x = 1\\ \end{aligned} \right.
f(x)=⎩
⎨
⎧x211x=1x=1
(c)
f
(
x
)
=
{
x
2
−
x
−
2
x
−
2
x
≠
2
1
x
=
2
f(x)=\left\{ \begin{aligned} & \frac{x^2 - x - 2}{x - 2} & x \neq 2\\ & 1 & x = 2\\ \end{aligned} \right.
f(x)=⎩
⎨
⎧x−2x2−x−21x=2x=2
(d)
f
(
x
)
=
⌊
x
⌋
f(x) = \lfloor x \rfloor
f(x)=⌊x⌋(向下取整)
解:
(a) 函数在
x
=
2
x = 2
x=2处不连续,因为不在定义域内;
(b) 函数在
x
=
1
x = 1
x=1处不连续,因为
lim
x
→
1
f
(
x
)
\lim_{x \rightarrow 1}f(x)
limx→1f(x)不存在;
(c) 函数在
x
=
2
x = 2
x=2处不连续,因为
lim
x
→
2
f
(
x
)
=
lim
x
→
2
(
x
−
2
)
(
x
+
1
)
x
−
2
=
lim
x
→
2
(
x
+
1
)
=
3
≠
f
(
2
)
\lim_{x \rightarrow 2}f(x) = \lim_{x \rightarrow 2}\frac{(x - 2)(x + 1)}{x - 2} = \lim_{x \rightarrow 2}(x + 1) = 3 \neq f(2)
x→2limf(x)=x→2limx−2(x−2)(x+1)=x→2lim(x+1)=3=f(2)
(d) 函数在
x
x
x为整数的点不连续,因为这些点的极限不存在。(下面会证明)
如图所示,其中
(a)和(c)被称为可移除连续
(b)被称为无限不连续
(d)被称为跳跃不连续
定义 2 如果
lim
x
→
a
+
f
(
x
)
=
f
(
a
)
\lim_{x \rightarrow a^+}f(x) = f(a)
limx→a+f(x)=f(a),那么函数
f
f
f在
x
=
a
x = a
x=a的右侧连续;如果
lim
x
→
a
−
f
(
x
)
=
f
(
a
)
\lim_{x \rightarrow a^-}f(x) = f(a)
limx→a−f(x)=f(a),那么函数
f
f
f在
x
=
a
x = a
x=a的左侧连续。
例三:证明对于任意整数
n
n
n,函数
f
(
x
)
=
⌊
x
⌋
f(x) = \lfloor x \rfloor
f(x)=⌊x⌋在
x
=
n
x = n
x=n的右侧连续。
lim
x
→
n
+
f
(
x
)
=
lim
x
→
n
+
⌊
x
⌋
=
n
=
f
(
n
)
lim
x
→
n
−
f
(
x
)
=
lim
x
→
n
−
⌊
x
⌋
=
n
−
1
≠
f
(
n
)
\begin{aligned} & \lim_{x \rightarrow n^+}f(x) = \lim_{x \rightarrow n^+}{\lfloor x \rfloor} = n = f(n)\\ & \lim_{x \rightarrow n^-}f(x) = \lim_{x \rightarrow n^-}{\lfloor x \rfloor} = n - 1 \neq f(n)\\ \end{aligned}
x→n+limf(x)=x→n+lim⌊x⌋=n=f(n)x→n−limf(x)=x→n−lim⌊x⌋=n−1=f(n)
通过这个例子,我们可以看出
f
(
x
)
=
⌊
x
⌋
f(x) = \lfloor x \rfloor
f(x)=⌊x⌋在
x
x
x为整数的点上没有极限,因此不连续。
定义 3 如果函数 f f f在区间内任意点上连续,那么 f f f在该区间连续。(如果 f f f仅在区间端点的一侧定义,则我们将端点处的连续理解为从右侧连续或从左侧连续。)
例四:证明
f
(
x
)
=
1
−
1
−
x
2
f(x) = 1 - \sqrt{1 - x^2}
f(x)=1−1−x2在区间
[
−
1
,
1
]
[-1, 1]
[−1,1]连续。
解:
如果
−
1
<
a
<
1
-1 < a < 1
−1<a<1,那么根据前面的极限定律,有
lim
x
→
a
f
(
x
)
=
lim
x
→
a
(
1
−
1
−
x
2
)
=
1
−
lim
x
→
a
1
−
x
2
=
1
−
lim
x
→
a
(
1
−
x
2
)
=
1
−
1
−
a
2
=
f
(
a
)
\begin{aligned} \lim_{x \rightarrow a}f(x) & = \lim_{x \rightarrow a}(1 - \sqrt{1 - x^2}) \\ & = 1 - \lim_{x \rightarrow a} \sqrt{1 - x^2} \\ & = 1 - \sqrt{\lim_{x \rightarrow a}(1 - x^2)} \\ & = 1 - \sqrt{1 - a^2} \\ & = f(a) \end{aligned}
x→alimf(x)=x→alim(1−1−x2)=1−x→alim1−x2=1−x→alim(1−x2)=1−1−a2=f(a)
根据定义 1,
f
f
f在
a
a
a处连续,其中
−
1
<
a
<
1
-1 < a < 1
−1<a<1。另外
lim
x
→
−
1
+
f
(
x
)
=
1
=
f
(
−
1
)
lim
x
→
1
−
f
(
x
)
=
1
=
f
(
1
)
\begin{aligned} & \lim_{x \rightarrow -1^+}f(x) = 1 = f(-1) \\ & \lim_{x \rightarrow 1^-}f(x) = 1 = f(1) \end{aligned}
x→−1+limf(x)=1=f(−1)x→1−limf(x)=1=f(1)
根据定义 2,
f
f
f在
−
1
-1
−1右侧连续,在
1
1
1的左侧连续。因此,根据定义 3,
f
f
f在
[
−
1
,
1
]
[-1, 1]
[−1,1]上连续。
定理
定理 1 如果 f f f和 g g g在 a a a点连续,并且 c c c是一个常数,那么下面的函数同样在 a a a点连续:
- f + g f + g f+g
- f − g f - g f−g
- c f cf cf
- f g fg fg
- f g \frac{f}{g} gf \
证明
f
+
g
f+g
f+g也在
a
a
a处连续。
已知
lim
x
→
a
f
(
x
)
=
f
(
a
)
\lim_{x \rightarrow a}f(x) = f(a)
limx→af(x)=f(a)和
lim
x
→
a
g
(
x
)
=
g
(
a
)
\lim_{x \rightarrow a}g(x) = g(a)
limx→ag(x)=g(a)。
因此
lim
x
→
a
(
f
+
g
)
(
x
)
=
lim
x
→
a
[
f
(
x
)
+
g
(
x
)
]
=
lim
x
→
a
f
(
x
)
+
lim
x
→
a
g
(
x
)
=
f
(
a
)
+
g
(
a
)
=
(
f
+
g
)
(
a
)
\begin{aligned} \lim_{x \rightarrow a}(f + g)(x) &= \lim_{x \rightarrow a}[f(x) + g(x)] \\ &= \lim_{x \rightarrow a}f(x) + \lim_{x \rightarrow a}g(x) \\ &= f(a) + g(a) \\ &= (f + g)(a) \end{aligned}
x→alim(f+g)(x)=x→alim[f(x)+g(x)]=x→alimf(x)+x→alimg(x)=f(a)+g(a)=(f+g)(a)
所以
f
+
g
f + g
f+g在
a
a
a点连续。
定理 2
(a) 多项式在任意点连续;也就是说多项式在
(
−
∞
,
∞
)
(-\infty, \infty)
(−∞,∞)连续;
(b) 分数式在定义域连续;
(c) 根函数在定义域连续;
(d) 三角函数在定义域连续;
证明(a)
多项式的格式为
P
(
x
)
=
c
n
x
n
+
c
n
−
1
x
n
−
1
+
.
.
.
+
c
1
x
1
+
c
0
P(x) = c_nx^n + c_{n-1}x^{n-1} +...+ c_1x^1 + c_0
P(x)=cnxn+cn−1xn−1+...+c1x1+c0
其中
c
0
,
c
1
,
.
.
.
,
c
n
c_0, c_1,...,c_n
c0,c1,...,cn为常数。根据极限定律我们知道
lim
x
→
a
c
0
=
c
0
\lim_{x \rightarrow a}c_0 = c_0
x→alimc0=c0
lim
x
→
a
x
m
=
a
m
\lim_{x \rightarrow a}x^m = a^m
x→alimxm=am
由此可见,
f
(
x
)
=
x
m
f(x) = x^m
f(x)=xm是一个连续的函数。根据定理1-3,我们知道
g
(
x
)
=
c
x
m
g(x) = cx^m
g(x)=cxm也连续。因此,根据定理1-1可知
P
P
P连续。
例一:计算 lim x → π sin x 1 + cos x \lim_{x \rightarrow \pi}\frac{\sin x}{1 + \cos x} limx→π1+cosxsinx。
- 首先证明其连续;
- 然后根据定义 1求解。
定理 3 如果
f
f
f在
x
=
b
x = b
x=b处连续,并且
lim
x
→
a
g
(
x
)
=
b
\lim_{x \rightarrow a}g(x) = b
limx→ag(x)=b,那么
lim
x
→
a
f
(
g
(
x
)
)
=
f
(
b
)
\lim_{x \rightarrow a}f(g(x)) = f(b)
limx→af(g(x))=f(b)。也就是
lim
x
→
a
f
(
g
(
x
)
)
=
f
(
lim
x
→
a
g
(
x
)
)
\lim_{x \rightarrow a}f(g(x)) = f(\lim_{x \rightarrow a}g(x))
x→alimf(g(x))=f(x→alimg(x))
定理 4 如果 g g g在 a a a处连续, f f f在 g ( a ) g(a) g(a)处连续,那么复合函数 ( f ∘ g ) ( x ) = f ( g ( x ) ) (f \circ g)(x) = f(g(x)) (f∘g)(x)=f(g(x))在 a a a处连续。
证明
已知
lim
x
→
a
g
(
x
)
=
g
(
a
)
\lim_{x \rightarrow a}g(x) = g(a)
x→alimg(x)=g(a)
根据定理 3,有
lim
x
→
a
f
(
g
(
x
)
)
=
f
(
g
(
a
)
)
\lim_{x \rightarrow a}f(g(x)) = f(g(a))
x→alimf(g(x))=f(g(a))
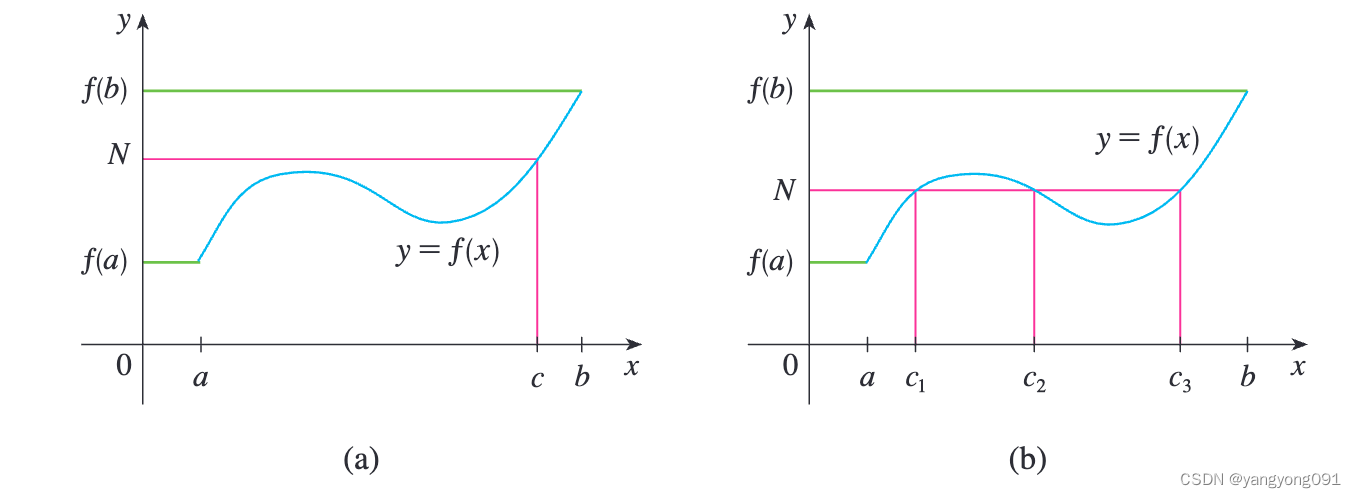
中值定理 5 假设 f f f在 [ a , b ] [a, b] [a,b]连续,令 N N N处于 f ( a ) f(a) f(a)和 f ( b ) f(b) f(b)中间,其中 f ( a ) ≠ f ( b ) f(a) \neq f(b) f(a)=f(b)。那么存在 c c c属于 ( a , b ) (a, b) (a,b),使得 f ( c ) = N f(c) = N f(c)=N。
如图所示
练习题
- 根据定理,说明函数为什么在其定义域内连续,并指出其定义域。
B ( x ) = tan x 4 − x 2 B(x) = \frac{\tan x}{\sqrt{4 - x^2}} B(x)=4−x2tanx - 根据连续性计算极限。
lim x → π sin ( x + sin x ) \lim_{x \rightarrow \pi}\sin(x + \sin x) x→πlimsin(x+sinx) - 证明
f
f
f在
(
−
∞
,
∞
)
(-\infty, \infty)
(−∞,∞)上连续。
f ( x ) = { 1 − x 2 x ≤ 1 x − 1 x > 1 f(x) = \left\{ \begin{aligned} & 1 - x^2 & x \leq 1 \\ & \sqrt{x - 1} & x > 1 \end{aligned} \right. f(x)={1−x2x−1x≤1x>1 - 找出不连续的点,说明在这些点上是左侧连续还是右侧连续,并且画出图像。
f ( x ) = { x 2 x < − 1 x − 1 ≥ x < 1 1 / x x ≥ 1 f(x) = \left\{ \begin{aligned} & x^2 & x < -1 \\ & x & -1 \geq x < 1 \\ & 1/x & x \geq 1 \end{aligned} \right. f(x)=⎩ ⎨ ⎧x2x1/xx<−1−1≥x<1x≥1 - 地心引力方程如下,请问
F
F
F在
r
=
R
r = R
r=R处连续吗?
F ( r ) = { G M r R 3 r < R G M r 2 r ≥ R F(r) = \left\{ \begin{aligned} & \frac{GMr}{R^3} & r < R \\ & \frac{GM}{r^2} & r \geq R \end{aligned} \right. F(r)=⎩ ⎨ ⎧R3GMrr2GMr<Rr≥R - 找出常量
c
c
c,使得
f
f
f在
(
−
∞
,
∞
)
(-\infty, \infty)
(−∞,∞)连续。
f ( x ) = { c x 2 + 2 x x < 2 x 3 − c x x ≥ 1 f(x) = \left\{ \begin{aligned} & cx^2 + 2x & x < 2 \\ & x^3 - cx & x \geq 1 \end{aligned} \right. f(x)={cx2+2xx3−cxx<2x≥1 - 根据中值定理,证明下面的式子有解。
sin x = x 2 − x \sin x = x^2 - x sinx=x2−x - 证明当前仅当 lim h → 0 f ( a + h ) = f ( a ) \lim_{h \rightarrow 0}f(a + h) = f(a) limh→0f(a+h)=f(a)时, f f f在 a a a处连续。
- 使用上面的结论证明 sin x \sin x sinx在任意 a a a处连续。
- 一个僧人一天早上7点从寺庙向山顶出发,晚上7点到达山顶。第二天早上7点从山顶向寺庙出发,走同样路线,晚上7点到达寺庙。请使用中值定理证明路径上有一个点,僧人两天在同一时刻穿过该点。






















 996
996

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








